邻接矩阵-建立图

1.介绍图的相关概念

　　图是由顶点的有穷非空集和一个描述顶点之间关系-边（或者弧）的集合组成。通常，图中的数据元素被称为顶点，顶点间的关系用边表示，图通常用字母G表示，图的顶点通常用字母V表示，所以图可以定义为:

　　G=(V,E)

其中，V(G)是图中顶点的有穷非空集合，E(G)是V(G)中顶点的边的有穷集合

1.1 无向图：图中任意两个顶点构成的边是没有方向的

1.2 有向图：图中任意两个顶点构成的边是有方向的，通常有向图的边也称之为弧

1.3 完全图：图中任意一个顶点与其他节点之间都有边

1.4 稠密图、稀疏图：一个图接近完全图称为稠密图，边数很少的图称为稀疏图

1.6 顶点的度：依附于某顶点的边数称为该顶点的度，在有向图中，以顶点为终点的弧的数目为该顶点的入度，以该点为始点的弧数为该顶点的出度

1.7 权：图中与边或弧有关的数据信息

1.8 网：边上带权的图称为网或带权图

1.9 路径、路径长度:无向图中，从任意一点到另一点所经过的顶点序列称为路径，路径上的边数称为路径长度

2.0 简单路径、简单回路、回路：一条路径中，若路径序列中所有顶点除起始点和中止点之外，彼此都不同，则该路径为简单路径。简单路径中的起始点与中止点相同，该路径为简单回路。如果路径序列中起始点与中止点相同，则该路径为回路或者环。

2.1 连通、连通图：无向图中，某两顶点之间有路径，则称这两个顶点是连通的。如果图中任意两顶点都是连通的，则该无向图为连通图，否则为非连通图。

2.2 极大连通子图、连通分量：如果在向无向连通图中加入原图的任何一个顶点，子图就不连通，则为极大连通分量。无向连通图中的极大连通子图称为该无向图的连通分量。/在有向图中若任意两顶点存在两条弧（一个入度一个出度），则称为强连通图，强连通分量同理。

图G的三个连通分量：

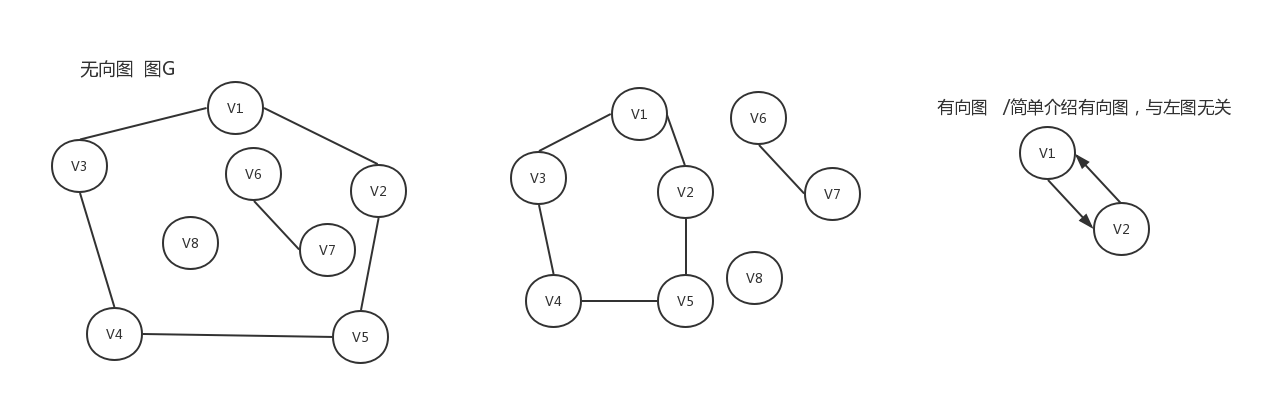
2.图的存储

邻接矩阵是表示顶点间相邻关系的矩阵，无向图中，如果两顶点有边，则G[i][j] = G[j][i] = 1,反之为0,有向图中G[i][j] = 1,但是G[j][i] 未必等于1

也可以表示带权图，即将1换位权值即可

程序：

 1 //建立图的邻接矩阵算法程序 /有向图，无权值，两顶点之间有边就用1表示，无边用0表示 
 2 #include<stdio.h>
 3 #include<string.h>
 4 #define MAX_VEX 100 
 5 
 6 int creatcost(int cost[][MAX_VEX])             //*cost数组表示所有带权图的邻接矩阵 
 7 {
 8     int vexnum,arcnum,i,j,k,v1,v2;             //输入图的顶点数和边数（或弧数）
 9 
10     printf("\n请输入顶点数，边数:\n");
11     scanf("%d %d",&vexnum,&arcnum);
12     for(i = 1;i <= vexnum;i++)                 //初始化带权图的邻接矩阵
13         for(j = 1;j <= vexnum;j++)
14             cost[i][j] = 0;                    //0表示无穷大
15     //memset(cost,0,vexnum*vexnum);            //也可以使用memset()函数进行初始化，将整个矩阵置0，需要有文件string.h 
16     for(k = 0;k < arcnum;k++)
17     {
18         printf("v1,v2= ");
19         scanf("%d %d",&v1,&v2);
20         cost[v1][v2] = 1;
21         //cost[v2][v1] = 1;                    //若建立无向图的邻接矩阵就应该加上这句话 
22     } 
23     
24     return vexnum; 
25 }
26 
27 int main()
28 {
29     int i,j,vexnum;
30     int cost[MAX_VEX][MAX_VEX];
31     vexnum = creatcost(cost);
32     printf("所建图的邻接矩阵为:\n");
33     for(i = 1;i <= vexnum;i++)
34     {
35         for(j = 1;j <= vexnum;j++)
36             printf("%3d",cost[i][j]);
37         printf("\n");
38     }
39     
40     return 0;
41 }