AtCoder Grand Contest 017
A - Biscuits
有\(n\)个数,问有多少个集合的数的和模\(2\)余\(P\)。
随便\(dp\)一下就好了。
#include<iostream>
#include<cstdio>
using namespace std;
#define ll long long
inline int read()
{int x=0;bool t=false;char ch=getchar();while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();if(ch=='-')t=true,ch=getchar();while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();return t?-x:x;
}
int n,P;ll f[55][2];
int main()
{n=read();P=read();f[0][0]=1;for(int i=1;i<=n;++i){int x=read()&1;f[i][0]=f[i-1][0];f[i][1]=f[i-1][1];f[i][0^x]+=f[i-1][0];f[i][1^x]+=f[i-1][1];}printf("%lld\n",f[n][P]);return 0;
}B - Moderate Differences
有\(n\)个数排成一行,第一个数是\(A\),最后一个数是\(B\),已知相邻的两个数的差的绝对值都在\([C,D]\)之间,问是否存在一个合法的情况。
显然每个数要么贡献为正要么贡献为负,那么枚举有多少个贡献为正,这样子就能够算出一个合法区间,判断\(B-A\)是否在这个区间内就行了。
#include<iostream>
#include<cstdio>
using namespace std;
#define ll long long
inline int read()
{int x=0;bool t=false;char ch=getchar();while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();if(ch=='-')t=true,ch=getchar();while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();return t?-x:x;
}
int n,A,B,C,D;
ll L,R;
void chk(){if(L<=B&&B<=R)puts("YES"),exit(0);}
int main()
{n=read();A=read();B=read()-A;C=read();D=read();for(int i=0;i<n;++i){L=1ll*C*i-1ll*(n-1-i)*D;R=1ll*D*i-1ll*(n-1-i)*C;chk();}puts("NO");return 0;
}C - Snuke and Spells
你有\(n\)个球,假设当前剩下的球的个数是\(k\)个,那么就把所有球上写的数字为\(k\)的球给丢掉。
现在你可以改变一些球上的数字,问最少改变多少次可以让所有球都被删掉。
有若干次修改,你要对于每次修改之后都求出答案。
我怎么觉得这题做过啊。。。。
大概就是把数字个数用类似柱状图给表示出来,然后把柱子给向左推倒,那么\([1,n]\)中未被覆盖的位置的个数的就是答案。
那么拿线段树模拟一下就行了嗷。
#include<iostream>
#include<cstdio>
using namespace std;
#define MAX 200200
inline int read()
{int x=0;bool t=false;char ch=getchar();while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();if(ch=='-')t=true,ch=getchar();while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();return t?-x:x;
}
int n,Q;
int a[MAX],b[MAX],c[MAX];
#define lson (now<<1)
#define rson (now<<1|1)
int t[MAX<<2],mn[MAX<<2];
void pushup(int now){mn[now]=mn[lson]+mn[rson];}
void Build(int now,int l,int r)
{if(l==r){t[now]=c[l];mn[now]=c[l]==0;return;}int mid=(l+r)>>1;Build(lson,l,mid);Build(rson,mid+1,r);pushup(now);
}
void Modify(int now,int l,int r,int p,int w)
{if(l==r){t[now]+=w;mn[now]=t[now]==0;return;}int mid=(l+r)>>1;if(p<=mid)Modify(lson,l,mid,p,w);else Modify(rson,mid+1,r,p,w);pushup(now);
}
int main()
{n=read();Q=read();for(int i=1;i<=n;++i)b[a[i]=read()]++;for(int i=1;i<=n;++i)if(b[i])c[max(1,i-b[i]+1)]+=1,c[i+1]-=1;for(int i=1;i<=n;++i)c[i]+=c[i-1];Build(1,1,n);while(Q--){int x=read(),v=read();b[a[x]]--;if(a[x]-b[a[x]]>0)Modify(1,1,n,a[x]-b[a[x]],-1);a[x]=v;if(a[x]-b[a[x]]>0)Modify(1,1,n,a[x]-b[a[x]],1);b[a[x]]++;printf("%d\n",mn[1]);}return 0;
}D - Game on Tree
两个人在一棵\(n\)个节点的树上玩游戏,每次可以选择一条边,把这条边删掉,然后把不包含\(1\)的那个连通块给删掉,不能操作者输。
问谁会赢。
emmmm,这是个博弈题,所以如果不是神仙结论的话就往\(SG\)函数上靠。
显然根节点的每个儿子都可以拆下来变成一个子游戏,所以根节点的\(sg\)值就是所有儿子\(sg\)值的异或和。
因为所有儿子拆下来变成子游戏之后,还需要花\(1\)步把这个儿子删掉,所以每个点的\(sg\)值是所有儿子\(sg\)值\(+1\)的异或和。
#include<iostream>
#include<cstdio>
using namespace std;
#define MAX 100100
inline int read()
{int x=0;bool t=false;char ch=getchar();while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();if(ch=='-')t=true,ch=getchar();while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();return t?-x:x;
}
struct Line{int v,next;}e[MAX<<1];
int h[MAX],cnt=1;
inline void Add(int u,int v){e[cnt]=(Line){v,h[u]};h[u]=cnt++;}
int n,sg[MAX],vis[MAX];
void dfs(int u,int ff)
{for(int i=h[u];i;i=e[i].next)if(e[i].v!=ff)dfs(e[i].v,u),sg[u]^=sg[e[i].v]+1;
}
int main()
{n=read();for(int i=1;i<n;++i){int u=read(),v=read();Add(u,v);Add(v,u);}dfs(1,0);puts(sg[1]?"Alice":"Bob");return 0;
}E - Jigsaw
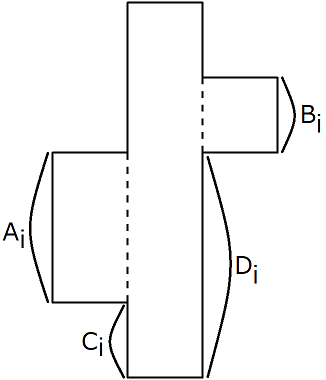
有若干个高度为\(H\)的积木,每个都长成这样:
且\(A_i,B_i,C_i,D_i\)都会告诉你,并且左中右三个部分的宽度也相等。
现在给你\(n\)个积木,你要让中间那部分的下面挨着地面,然后拼出来的东西要满足不存在地面上面的存在一段空,且这段空的上方还有积木。写成坐标的形式就是不存在\((x,y1)\)未被积木覆盖,但是\((x,y_2),y_1<y_2\)被积木覆盖了。
显然是考虑把一个积木左边给卡进另一个积木的右侧里,那么我们把能够卡的积木之间连边,把接地的和起点终点连边,于是就是问所有积木是否能分成若干条路径。然而这样子复杂度很假,因为边数可以达到\(O(n^2)\)级别。
考虑把积木看成边,于是我们可以把左侧\(C_i=0\)看成点\(-A_i\),\(C_i\neq 0\)看成点\(C_i\),右侧\(D_i=0\)看成点\(B_i\),\(D_i\neq 0\)看成\(-D_i\)。这样转化完之后一个积木就是一条边,于是问题变成了我们有\([-H,H]\)这些点,之间有一些边,我们要把每一条边都划分进一个路径中,使得路径以负数为起点,以正数为终点。
那么我们统计入度和出度,显然负数的入度不能多于出度,正数出度不能多于入度。同时这个东西不能成环,所以一个连通块中至少存在一个点入度不等于出度。
#include<iostream>
#include<cstdio>
using namespace std;
#define MAX 450
inline int read()
{int x=0;bool t=false;char ch=getchar();while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();if(ch=='-')t=true,ch=getchar();while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();return t?-x:x;
}
int n,H,f[MAX],In[MAX],Ot[MAX];bool vis[MAX];
int getf(int x){return x==f[x]?x:f[x]=getf(f[x]);}
int main()
{n=read();H=read();for(int i=1;i<=H+H;++i)f[i]=i,vis[i]=false;for(int i=1;i<=n;++i){int a=read(),b=read(),c=read(),d=read();int l=(c>0?c:-a)+H,r=(d>0?-d:b)+H;if(getf(l)!=getf(r))f[getf(l)]=getf(r);In[r]+=1;Ot[l]+=1;}for(int i=-H;i<0;++i)if(In[i+H]>Ot[i+H]){puts("NO");return 0;}for(int i=1;i<=H;++i)if(In[i+H]<Ot[i+H]){puts("NO");return 0;}for(int i=0;i<=H+H;++i)if(In[i]!=Ot[i])vis[getf(i)]=true;for(int i=0;i<=H+H;++i)if(In[i]&&Ot[i]&&!vis[getf(i)]){puts("NO");return 0;}puts("YES");return 0;
}F - Zigzag
有\(n*(n+1)/2\)个点,第\(i\)行有\(i\)个点,用\((i,j),j\le i\)表示这些点。
从\((i,j)\)只能走到\((i+1,j+1)\)或者\((i+1,j)\)。
现在你要找到\(m\)条从\((1,1)\)走到第\(n\)行的路径,假设第\(a\)条路径走过的第\(k\)个点是\((k,X[a,k])\),那么对于任意的\(a\le b\),不能存在\(i\)使得\(X[a,i]>X[b,i]\)。
同时还有\(k\)个限制,每个限制形如\((a,b,c)\)表示第\(a\)条路径的第\(b\)个点到第\(b+1\)个点必须朝着\(c\)方向走。
问方案数。
首先一条路径可以用一个二进制数来表示,那么一个暴力做法就是枚举上一个二进制数再枚举这一个,复杂度大概可以做到\(O(2^{2n})\)。
考虑优化这个过程。注意到我们的合法情况是前一个的前缀和在任意时刻都不大于后一个的前缀和。
假设现在正在确定第\(i\)条路径,且前\(j-1\)位已经确定完毕并且和\(i-1\)的前\(j-1\)位相同,现在正在确定第\(j\)位。
如果这一位相同,过,没啥事。否则不同,根据前面的要求,只能是\(i-1\)的这一位是\(0\),\(i\)的这一位是\(1\)。
那么我们找到\(i-1\)的下一个\(1\)的位置,把这个\(1\)推上来,推到\(j\)位置,强行和\(i\)的前\(j\)位相同,不难发现这样子处理完毕之后对于\(i\)而言,到下一个\(i-1\)存在\(1\)的位置之前,是没有任何影响的,因为这一位多了一个\(1\),而后面都是\(0\),所以怎么填都是合法的。于是我们就把这个状态的前\(j-1\)位转移到了\(j\)位了。
如果下一个\(1\)不存在,那么接下来\(i\)就可以任意走了。
那么就这样子直接\(dp\)就好了。
设\(f[i][j][S]\)表示当前考虑到第\(i\)位,前\(j\)位和\(i-1\)的状态相同,\(i-1\)的\(01\)状态是\(S\)的方案数。
转移的时候枚举这一位填什么,如果填\(0\)而\(S\)这一位是\(1\)则不合法。如果两个相等则直接转移;否则按照前面说的减掉下一个\(1\)再转移。
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define MOD 1000000007
void add(int &x,int y){x+=y;if(x>=MOD)x-=MOD;}
inline int read()
{int x=0;bool t=false;char ch=getchar();while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();if(ch=='-')t=true,ch=getchar();while(ch<='9'&&ch>='0')x=x*10+ch-48,ch=getchar();return t?-x:x;
}
int n,m,K,ans,Lim[22][22];
int f[2][22][1<<20],nxt[1<<20][22];
int main()
{n=read()-1;m=read();K=read();memset(Lim,-1,sizeof(Lim));for(int i=1;i<=K;++i){int a=read(),b=read();Lim[a][b-1]=read();}int S=1<<n;for(int i=0;i<S;++i){int v=-1;for(int j=n-1;~j;--j){if(i&(1<<j))v=j;nxt[i][j]=v;}}f[0][n][0]=1;for(int i=1,nw=1,pw=0;i<=m;++i,nw^=1,pw^=1){for(int j=0;j<S;++j)f[nw][0][j]=f[pw][n][j];memset(f[pw],0,sizeof(f[pw]));for(int j=0;j<n;++j)for(int k=0;k<S;++k)if(f[nw][j][k])for(int l=0;l<=1;++l){if((~Lim[i][j])&&l!=Lim[i][j])continue;int t=(k>>j)&1;if(l==0&&t==1)continue;if(l==t)add(f[nw][j+1][k],f[nw][j][k]);else{int p=nxt[k][j];if(p==-1)add(f[nw][j+1][k+(1<<j)],f[nw][j][k]);else add(f[nw][j+1][k+(1<<j)-(1<<p)],f[nw][j][k]);}}}for(int i=0;i<S;++i)add(ans,f[m&1][n][i]);printf("%d\n",ans);return 0;
}
















)


