Sigmoid函数

Sigmoid函数计算公式

$f(x) = \frac{1}{1+e^{-x}}$

sigmoid：x取值范围(-∞，+∞)，值域是(0, 1)。

sigmoid函数求导

这是sigmoid函数的一个重要性质。

$\begin{aligned}g(z)&=\frac{1}{1+e^{-z}} \\g'(z)&=(\frac{1}{1+e^{-z}})' \\&=\frac{e^{-z}}{(1+e^{-z})^2} \\&=\frac{1}{1+e^{-z}}\cdot\frac{e^{-z}}{1+e^{-z}} \\&=\frac{1}{1+e^{-z}}\cdot(1-\frac{1}{1+e^{-z}}) \\&=g(z)\cdot(1-g(z))\end{aligned}$

图像

å¨è¿éæå¥å¾çæè¿°

代码

# -*- coding: utf-8 -*-
"""
@author: tom
"""import numpy
import math
import matplotlib.pyplot as pltdef sigmoid(x):a = []for item in x:a.append(1.0/(1.0 + math.exp(-item)))return ax = numpy.arange(-10, 10, 0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.show()

当x为0时，Sigmoid函数值为0.5。随着x的增大，对应的Sigmoid值将逼近于1；而随着x的减小，Sigmoid值将逼近于0。两种坐标尺度下的Sigmoid函数图。上图的横坐标为-5到5，这时的曲线变化较为平滑；下图横坐标的尺度足够大，可以看到，在x = 0点处Sigmoid函数看起来很像阶跃函数，如果横坐标刻度足够大（上图中的下图），Sigmoid函数看起来很像一个阶跃函数。

sigmoid函数的性质

sigmoid函数是一个阀值函数，不管x取什么值，对应的sigmoid函数值总是0<sigmoid(x)<1。
sigmoid函数严格单调递增，而且其反函数也单调递增
sigmoid函数连续
sigmoid函数光滑
sigmoid函数关于点(0, 0.5)对称
sigmoid函数的导数是以它本身为因变量的函数，即f(x)' = F(f(x))

sigmoid函数Logistic函数

对于分类问题，需要找到一个单调可微函数将真实值与广义线性回归模型的预测值联系起来，这个函数就是Logistic函数，或者称Sigmoid函数。（单位阶跃函数不连续，且瞬间跳跃的过程很难处理）

原因参考https://zhuanlan.zhihu.com/p/59137998

Logistic/Sigmoid函数是一个常见的S型函数，适合于提供概率的估计以及依据这些估计的二进制响应；由于其单调递增、反函数单调递增、任意阶可导等性质，且可以将变量映射到(0, 1)之间，在逻辑回归、神经网络中有着广泛的应用。

sigmod作为激活函数优缺点

优点：

Sigmoid的取值范围在(0, 1)，而且是单调递增，比较容易优化
Sigmoid求导比较容易，可以直接推导得出。

缺点：

Sigmoid函数收敛比较缓慢
容易饱和（就是梯度消失之后，使用BP算法优化时这个神经元没有变化）和终止梯度传递(“死神经元”)；
Sigmoid函数并不是以（0,0）为中心点

tanh函数(双曲正切函数)

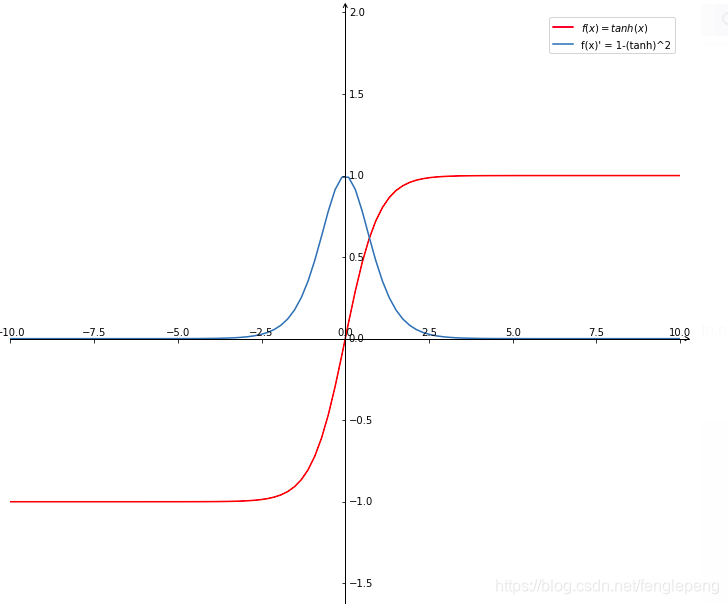
tanh为双曲正切函数，过（0,0）点。相比Sigmoid函数，更倾向于用tanh函数

$f(x) = tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$

x取值范围(-∞，+∞)，值域是(-1, 1)。

tanh求导

$\begin{aligned}\cfrac{{\rm d}y}{{\rm d}x} &= \left(\cfrac{e^x-e^{-x}}{e^x+e^{-x}}\right)^\prime \\&= \cfrac{(e^x-e^{-x})^\prime(e^x+e^{-x})-(e^x-e^{-x})(e^x+e^{-x})^\prime}{(e^x+e^{-x})^2} \\&= \cfrac{(e^x+e^{-x})(e^x+e^{-x})-(e^x-e^{-x})(e^x-e^{-x})}{(e^x+e^{-x})^2} \\&= \cfrac{e^{2x}+e^{-2x}+2-(e^{2x}+e^{-2x}-2)}{(e^x+e^{-x})^2} \\&= \cfrac{4}{(e^x+e^{-x})^2} \end{aligned}$

又因为

$1 - y = 1 - \cfrac{e^x-e^{-x}}{e^x+e^{-x}} = \cfrac{e^x+e^{-x}-(e^x-e^{-x})}{e^x+e^{-x}} = \cfrac{2e^{-x}}{e^x+e^{-x}}$
$1 + y = 1 + \cfrac{e^x-e^{-x}}{e^x+e^{-x}} = \cfrac{e^x+e^{-x}+(e^x-e^{-x})}{e^x+e^{-x}} = \cfrac{2e^{x}}{e^x+e^{-x}}$

所以

$(1 - y)(1+y) = 1 - y^2 = \cfrac{4}{(e^x+e^{-x})^2} = \cfrac{{\rm d}y}{{\rm d}x}$

即： $y = {\rm tanh}^\prime(x)=1-{\rm tanh}^2(x)$

或者

$f(x)=\frac{sinh(x)}{cosh(x)}=\frac{1-e^{-2x}}{1+e^{-2x}}=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}=\frac{e^{2x}-1}{e^{2x}+1}=2sigmoid(2x)-1$

$f^{'}(x)=tanh{'}(x)=sech^{2}(x)=1-tanh^{2}(x)$

tanh优缺点

优点：

输出以（0,0）为中心、取值范围(-1~1)、易理解
收敛速度相对于Sigmoid更快

缺点：

该导数在正负饱和区的梯度都会接近于 0 值，会造成梯度消失。还有其更复杂的幂运算。

图像

代码

import math
import matplotlib.pyplot as plt
import numpy as np
import mpl_toolkits.axisartist as axisartist# Tanh 激活函数
class Tanh:       # 原函数 def forward(self, x):return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))# 导数def backward(self, outx):tanh = (np.exp(outx) - np.exp(-outx)) / (np.exp(outx) + np.exp(-outx))return 1 - math.pow(tanh, 2)# 画图
def Axis(fig, ax):#将绘图区对象添加到画布中fig.add_axes(ax)# 隐藏坐标抽ax.axis[:].set_visible(False)# new_floating_axis 创建新的坐标ax.axis["x"] = ax.new_floating_axis(0, 0)# 给 x 轴创建箭头线，大小为1.0ax.axis["x"].set_axisline_style("->", size = 1.0)# 给 x 轴箭头指向方向ax.axis["x"].set_axis_direction("top")# 同理，创建 y 轴ax.axis["y"] = ax.new_floating_axis(1, 0)ax.axis["y"].set_axisline_style("->", size = 1.0)ax.axis["y"].set_axis_direction("right")# 返回间隔均匀的100个样本，计算间隔为[start, stop]。
x =  np.linspace(-10, 10, 100)
y_forward = []
y_backward = []def get_list_forward(x):for i in range(len(x)):y_forward.append(Tanh().forward(x[i]))return y_forwarddef get_list_backward(x):for i in range(len(x)):y_backward.append(Tanh().backward(x[i]))return y_backwardy_forward = get_list_forward(x)
y_backward = get_list_backward(x)#创建画布
fig = plt.figure(figsize=(12, 12))#创建绘图对象ax
ax = axisartist.Subplot(fig, 111)
Axis(fig, ax)# 设置x, y轴范围
plt.ylim((-2, 2))
plt.xlim((-10, 10))# 原函数，forward function
plt.plot(x, y_forward, color='red', label='$f(x) = tanh(x)$')
plt.legend()# 导数， backward function
plt.plot(x, y_backward, label='f(x)\' = 1-(tanh)^2')
plt.legend()plt.show()

ReLU函数(The Rectified Linear Unit, 修正线性单元函数)

公式如下：

$ReLU = f(x) = max(0,x)=\left\{\begin{matrix} 0,x\leq 0\\x,x>0 \end{matrix}\right.$

${f(x)}' =\left\{\begin{matrix} 0,x\leq 0\\1,x>0 \end{matrix}\right.$

图形图像：对于输入的x以0为分界线，左侧的均为0，右侧的为y=x这条直线

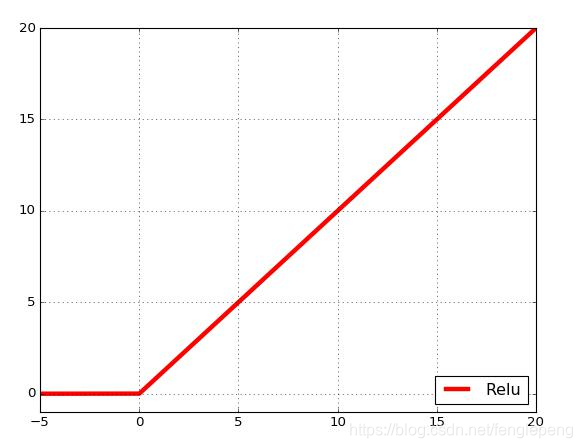
优缺点

优点：

在SGD中收敛速度要比Sigmoid和tanh快很多
梯度求解公式简单，不会产生梯度消失和梯度爆炸
对神经网络可以使用稀疏表达
对于无监督学习，也能获得很好的效果

缺点：

没有边界，可以使用变种ReLU: min(max(0,x), 6)
比较脆弱，比较容易陷入出现”死神经元”的情况，比如我们设置一个特别大学习率，经过一次更新权重参数w之后，w对于后续所有的输入x的结果都小于0，这个时候再进过relu激活，输出还是0，就会造成这个ReLU神经元对后来来的输入永远都不会被激活，同时，在反向传播时，在计算这个神经元的梯度永远都会是0，造成不可逆的死亡。（解决方案：较小的学习率）

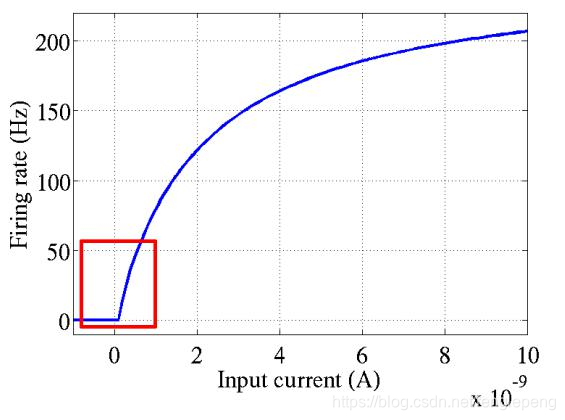
ReLU函数是从生物学角度，模拟出脑神经元接收信号更加准确的激活模型。相比于Sigmoid函数，具有以下优点：

单侧抑制；
相对宽阔的兴奋边界；
稀疏激活性；
更快的收敛速度；

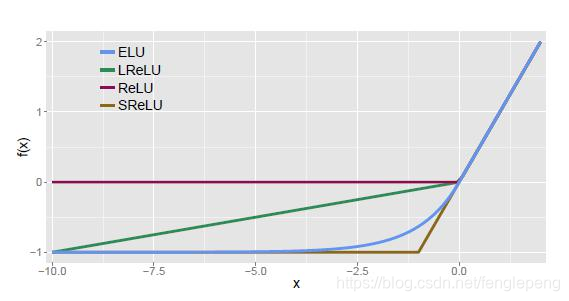
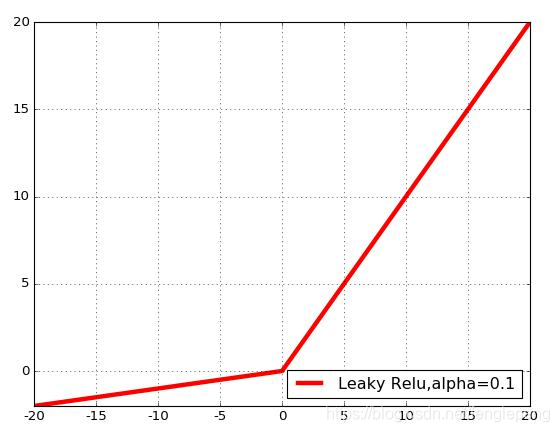
Leaky ReLU激活函数：

在ReLU函数的基础上，对x≤0的部分进行修正；目的是为了解决ReLU激活函数中容易存在的”死神经元”情况的；不过实际场景中：效果不是太好。

$Leaky ReLU = f(x) = max(0,x)=\left\{\begin{matrix} ax,x\leq 0\\x,x>0 \end{matrix}\right.$

${f(x)}' =\left\{\begin{matrix} a,x\leq 0\\1,x>0 \end{matrix}\right.$

ELU激活函数：

指数线性激活函数，同样属于对ReLU激活函数的x≤0部分的转换进行指数修正，而不是和Leaky ReLU中的线性修正。

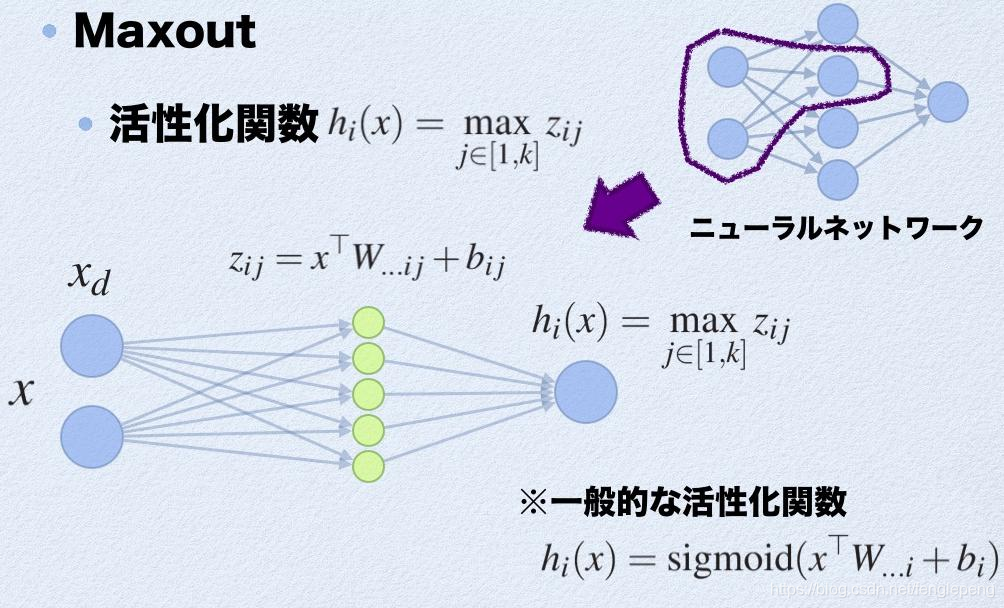
$ELU = f(x) = max(0,x)=\left\{\begin{matrix} a(e^x-1),x\leq 0\\x,x>0 \end{matrix}\right.$

${f(x)}' =\left\{\begin{matrix} f(x)+a,x\leq 0\\1,x>0 \end{matrix}\right.$

Maxout激活函数：

参考：https://arxiv.org/pdf/1302.4389.pdf

$maxout=f(x)=max_{j\in [1,k]}\{w_{j}x+b_{j}\}$

可以看作是在深度学习网络中加入一层激活函数层，包含一个参数k，拟合能力特别强。特殊在于：增加了k个神经元进行激活，然后输出激活值最大的值。

优点：

计算简单，不会出现神经元饱和的情况
不容易出现死神经元的情况

缺点：

参数double，计算量复杂了

激活值 out = f(W.X+b); f是激活函数。’.’在这里代表內积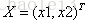这里写图片描述 ; W = () 那么当我们对（i+1）层使用maxout（设定k=5）然后再输出的时候，情况就发生了改变

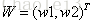
此时网络形式上就变成上面的样子，用公式表现出来就是：

z1 = W1.X+b1;
z2 = W2.X+b2;
z3 = W3.X+b3;
z4 = W4.X+b4;
z5 = W4.X+b5;
out = max(z1,z2,z3,z4,z5);

也就是说第（i+1）层的激活值计算了5次，可我们明明只需要1个激活值，那么我们该怎么办？其实上面的叙述中已经给出了答案，取这5者的最大值来作为最终的结果。

总结一下，maxout明显增加了网络的计算量，使得应用maxout的层的参数个数成k倍增加，原本只需要1组就可以，采用maxout之后就需要k倍了。

软饱和和硬饱和

假设h（x）是一个激活函数。

当我们的n趋近于正无穷，激活函数的导数趋近于0，那么我们称之为右饱和。
当我们的n趋近于负无穷，激活函数的导数趋近于0，那么我们称之为左饱和。
当一个函数既满足左饱和又满足右饱和的时候我们就称之为饱和，典型的函数有Sigmoid，Tanh函数。
对于任意的x，如果存在常数c，当x>c时，恒有=0，则称其为右硬饱和。如果对于任意的x，如果存在常数c，当x<c时，恒有=0,则称其为左硬饱和。既满足左硬饱和又满足右硬饱和的我们称这种函数为硬饱和。
对于任意的x，如果存在常数c，当x>c时，恒有趋近于0，则称其为右软饱和。如果对于任意的x，如果存在常数c，当x<c时，恒有趋近于0,则称其为左软饱和。既满足左软饱和又满足右软饱和的我们称这种函数为软饱和。