kd树就是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构,可以运用在k近邻法中,实现快速k近邻搜索。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分。
假设数据集\(T\)的大小是\(m*n\),即\(T={x_1,x_2,...x_m}\),其中\(x_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(n)})^T,i=1,2,...m\)。构建Kd树的过程大致如下。
对所有的数据,以\(x^{(1)}\)为轴,即取\(x_i^{(1)},i=1,2,...m\),并求得其中位数\(mid^{(1)}\),\(mid^{(1)}\)对应的点即为根节点,以\(mid^{(1)}\)为切分点,将剩余数据分为两个集合,左子树对应小于切分点的区域,右子树对应大于切分点的区域,然后针对每个集合,以\(x^{(2)}\)为轴,重复上述过程,继续切分为两个集合,然后不断重复上述过程,依次选择\(x^{(j)},j=1,2,...,n\)为轴,直到切分得到的集合中只有一个数据为止。
kd树的构造相对简单,那么如何利用kd树进行搜索?
给定一个目标点,搜索其最近邻,首先按照“左小右大”的规则,找到目标点所属区域对应的叶节点,然后从该叶节点出发,依次回退到父节点,不断查找与目标点最邻近的点,当确定不可能存在更近的节点时终止,这样搜索就被限制在空间的局部区域上,效率大大提高。
具体来说,
(1)从根节点出发,按照“左小右大”的规则,找到目标点所属区域对应的叶节点
(2)然后从该叶节点出发,向上回退,在回退到的每个父节点\(f\)上,执行一下两种操作:
(a)判断\(f\)与目标点的距离是否比当前最近距离更近,如果是,则将当前最近点更新为\(f\)
(b)当前最近点一定存在于\(f\)的一个子结点对应的区域中,即一定存在于\(f\)对应的区域中,即有可能\(f\)另一个 子结点距离目标点更近。判断目标点是否距离\(f\)另一个子结点对应区域更近,具体地,判断目标点与\(f\)对应的切 分轴 的距离是否小于当前最小距离,如果小于,从该子结点出发,重复执行步骤(2)
(3)当回退到根节点并完成对根节点步骤(2)中的两步操作时,搜索结束。当前最近点即为目标点的最近邻点。
以一个具体例子说明。如图1是生成的一颗kd树,特征空间划分如图2所示,要求目标点S(4.5,7.5)的最近邻点。
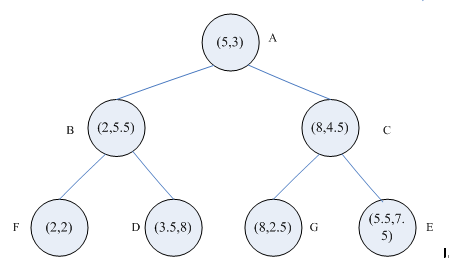
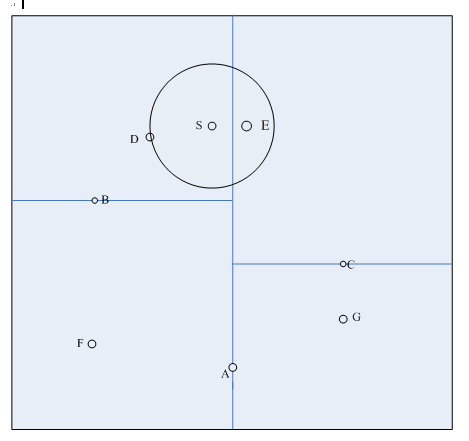
搜索过程如下:
(1)首先在kd树中找到了包含目标点S的叶节点D,D即为当前最近点,两点之间的距离是当前最近距离dist;
(2)向上回退到点B,点B距离点S更远,并且点B以\(x^{(2)}=5.5\)为切分轴,S距离\(x^{(2)}=5.5\)的距离大于dist,不用考虑点F;
(3)继续向上回退到根节点点A,点A距离点S更远,但是点A以\(x^{(1)}=5\)为切分轴,S距离\(x^{(1)}=5\)的距离小于dist,那么点S有可能距离A的右子树区域C中的点更近
(4)从点C出发,一直访问到点E,点E比点D距离点S更近,点E成为当前最近点,两点之间的距离是当前最近距离dist;
(5)从点E向上回退到点C,点C距离点S更远,并且点C以\(x^{(2)}=4.5\)为切分轴,S距离\(x^{(2)}=4.5\)的距离大于dist,不用考虑点G
(6)继续向上回退,再次回退到了根节点A,结束搜索,点E即为点S的最近邻点。

——数据库(二))



)




)

)





使用)
