每日微软面试题

每日微软面试题——day 1

<以下微软面试题全来自网络>

<以下答案与分析纯属个人观点，不足之处，还望不吝指出^_^>

题：.编写反转字符串的程序，要求优化速度、优化空间。

分析：构建两个迭代器p 和 q ，在一次遍历中，p的位置从字串开头向中间前进，q从字串末尾向中间后退，反转字串只要每次遍历都交换p和q所指向的内容即可，直到p和q在中间相遇，这时循环次数刚好等于字串的长度/2。

实现代码：

[cpp] view plaincopy

/**
author: 花心龟
blog：http://blog.csdn.net/zhanxinhang
**/
#include <stdio.h>
void reverse(char *_str,int _l) //反转函数,_l指要反转字串的长度
{
char *p=_str,*q=_str+_l-1,temp;
while(q>p)
{
temp=*p;
*p=*q;
*q=temp;
p++;
q--;
}
}
int main()
{
charstr0[11]= "0123456789";
reverse(str0,sizeof(str0)-1);
printf("str0 = %s\n",str0);
char str1[6]="01234";
reverse(str1,sizeof(str1)-1);
printf("str1 = %s",str1);
return 0;
}

题：.在链表里如何发现循环链接？

分析：可以构建两个迭代器p和pp，p一次向移动一个节点，pp一次移动两个节点，如果p和pp在某个时刻指向了同一个节点，那么该链表就有循环链接。

实现代码：

[cpp] view plaincopy

/**
Author:花心龟
Blog：http://blog.csdn.net/zhanxinhang
**/
#include <stdio.h>
#include <malloc.h>
#define TEST
struct list_node
{
int data;
list_node * next;
};
list_node *head; //指向头结点
void list_create()
{
int i;
list_node *p=NULL;
head = (list_node*)malloc(sizeof(list_node));
head->data=0; //头结点数据设为
head->next = NULL;
p=head;
for(i=1; i<6; i++) //创建个结点
{
p->next = (list_node*)malloc(sizeof(list_node));
p->next->data = i;
p->next->next = NULL;
p=p->next;
}
p->next = head; //使尾结点的下一个结点指针指向头结点，构成循环链表
#ifdef TEST
p=head;
for(i=0; i<12&&p!=NULL; i++)
{
printf("%d ",p->data);
p=p->next;
}
printf("\n");
#endif
}
void cycleList_test()
{
if(head==NULL || head->next == NULL)
return;
list_node *p=NULL,*pp=NULL;
p=head;
pp=head->next->next;
while(p!=pp )
{
p=p->next;
pp=pp->next->next;
if(p==NULL || pp==NULL)
{
printf("不是循环链表");
return ;
}
}
printf("是循环链表");
}
void list_destroy()
{
list_node *pmove=NULL,*pdel=NULL;
pmove=head->next;
while(pmove!=head)
{
pdel=pmove;
pmove=pmove->next;
free(pdel);
}
free(head);
}
int main()
{
list_create(); //构建循环链表
cycleList_test();//测试是否是循环链表
list_destroy(); //销毁链表
return 0;
}

题：.给出洗牌的一个算法，并将洗好的牌存储在一个整形数组里。

分析：首先54张牌分别用0到53 的数值表示并存储在一个整形数组里，数组下标代表纸牌所在的位置。接下来，遍历整个数组，在遍历过程中随机产生一个随机数，并以该随机数为下标的数组元素与当前遍历到的数组元素进行对换。时间复杂度为O(n) (注：所得到的每一种结果的概率的分母越大越好)

实现代码：

[cpp] view plaincopy

/**
Author:花心龟
Blog：http://blog.csdn.net/zhanxinhang
**/
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
void shuffle(int boke[]) //洗牌
{
int i,r,t;
srand((unsigned)time(NULL)); //随机数种子
for(i=0; i<54; i++)
{
r=(rand()%107)/2;
//交换
t=boke[i];
boke[i]=boke[r];
boke[r]=t;
}
}
int main()
{
int boke[54],i;
for(i=0;i<54;i++) //初始化纸牌
boke[i]=i;
printf("before shuffle:\n");
for(i=0; i<54; i++) //打印
printf("%d ",boke[i]);
shuffle(boke); //洗牌
printf("\nafter shuffle:\n");
for(i=0; i<54; i++) //打印
printf("%d ",boke[i]);
return 0;
}

题：写一个函数，检查字符串是否是整数，如果是，返回其整数值。

（或者：怎样只用4行代码编写出一个从字符串到长整形的函数？）

分析：略

实现代码：

[cpp] view plaincopy

/**
Author:花心龟
Blog：http://blog.csdn.net/zhanxinhang
**/
#include <stdio.h>
long convert(const char *str) // 4行代码？下面我用了四句语句，不知当不当否，权当娱乐^^
{
long value=0,f=1; //f将决定value是否为负数
if(*str == '-') str++,f=-1;
for(;*str!='\0' && *str>='0' && *str<='9'; str++)
value=value*10+(*str-'0');
return *str=='\0'?value*f:0; //如果不为整数返回
}
int main()
{
char str0[] = "1234567";
printf("%d\n",convert(str0));
char str1[] = "4.56";
printf("%d\n",convert(str1));
char str2[] = "-1234567";
printf("%d\n",convert(str2));
char str3[] = "-4.56";
printf("%d\n",convert(str3));
return 0;
}

题：怎样从顶部开始逐层打印二叉树结点数据？请编程。

分析：不用递归，定义两个栈(或数组)，也能方便漂亮地搞定。首先栈1存储第一层中的节点也就是根节点，然后每次循环，打印栈1中的元素，再将栈1中的节点更新为下一层中的节点。总共循环logn+1次。

实现代码（以下遗漏了对二叉树的销毁操作）：

[cpp] view plaincopy

/**
Author:花心龟
Blog：http://blog.csdn.net/zhanxinhang
**/
#include <stdio.h>
#include <malloc.h>
typedef struct bt_node
{
int data;
struct bt_node *rchild;
struct bt_node *lchild;
}BinTree,node_t;
BinTree *myTree;
node_t* bt_new_node(int data)
{
node_t* node = (node_t*)malloc(sizeof(node_t));
node->rchild = NULL;
node->lchild = NULL;
node->data = data;
return node;
}
void bt_create()
{
//第一层根节点，数字11表示第一层的第一个位置，以下类似
myTree = bt_new_node(11);
//创建第二层节点
myTree->lchild = bt_new_node(21);
myTree->rchild = bt_new_node(22);
//创建第三层节点
myTree->lchild->lchild = bt_new_node(31);
myTree->lchild->rchild = bt_new_node(32);
myTree->rchild->lchild = bt_new_node(33);
myTree->rchild->rchild = bt_new_node(34);
//创建第四层节点
myTree->rchild->rchild->rchild = bt_new_node(48);
}
void print_layer_by_layer() //逐层打印二叉树非递归算法(主题)
{
node_t* stack1[100]={0};//栈
node_t* stack2[100]={0};//栈
int T1=0,T2=0; //栈顶下标
stack1[T1++]=myTree; //根节点入栈
while(T1) //若栈为空则停止循环
{
while(T1)
{
T1--;
printf("%d ",stack1[T1]->data); //打印栈顶元素
stack2[T2++]=stack1[T1]; //将栈元素转存到栈2中
}
printf("\n");
//此时栈已存储了当前行的各元素
//通过栈得到下一行中的节点并更新到栈中
while(T2)
{
T2--;
if(stack2[T2]->rchild != NULL)
stack1[T1++]=stack2[T2]->rchild;
if(stack2[T2]->lchild != NULL)
stack1[T1++]=stack2[T2]->lchild;
}
}
}
int main()
{
bt_create(); //创建二叉树
print_layer_by_layer(); //逐层打印
return 0;
}

另：关于此题的其它想法请看3楼我的回复，回复上的编码步骤为广度优先遍历二叉树算法，不过本人不才哈，不知题目中的意思是一层一层的打印呢，还是按照层的顺序从左到右一个一个打印呢（好像也是逐层打印），且不管它，通过对两种算法比较，上面使用栈的算法功能更强，至少打完一层可以再打一个回行。而使用队列的广度优先遍历二叉树算法有效率优势，且代码简洁易懂，就是不能打完一层后回行。^_^ 纯属个人观点，望不吝指教。

题：怎样把一个链表掉个顺序（也就是反序，注意链表的边界条件并考虑空链表）？

分析：这题比较有意思，我想了个高效的实现。首先定义两个迭代器 p 和 q，q从第一个节点开始遍历，p从第二个节点开始遍历，每次遍历将头指针的next指向p的next，然后将p的next 反指向q(此时q是p的前一个节点)，也就是说将每个节点的链接方向掉过来，最后尾节点变成了头节点，头节点变成了尾节点，时间复杂度为高效的O(n)

图示：(最后一个N指空节点)

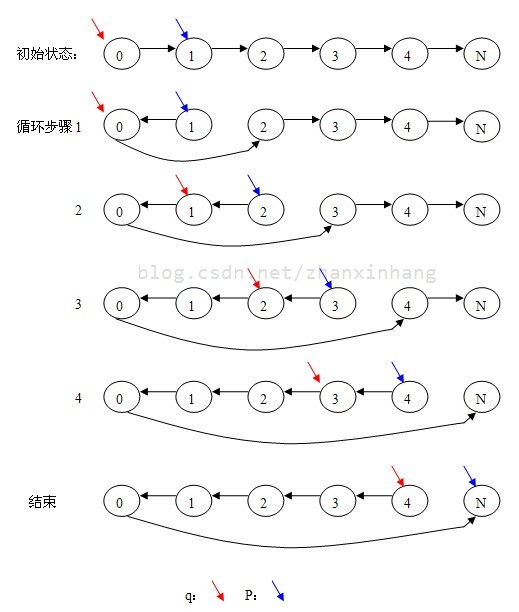
以下便是是我简洁的实现代码：

[cpp] view plaincopy

/**
Author:花心龟
Blog：http://blog.csdn.net/zhanxinhang
**/
#include <stdio.h>
#include <malloc.h>
#define TEST
typedef struct list_node
{
int data;
structlist_node * next;
}list_node;
list_node *head; //头结点
void list_create()
{
int i;
list_node *p;
head = (list_node*)malloc(sizeof(list_node));
head->data=0; //头结点数据设为
head->next = NULL;
p=head;
for(i=1;i<6; i++) //创建5个结点
{
p->next = (list_node*)malloc(sizeof(list_node));
p->next->data = i;
p->next->next = NULL;
p=p->next;
}
#ifdef TEST
p=head;
while(p!=NULL) //打印该链表
{
printf("%d",p->data);
p=p->next;
}
printf("\n");
#endif
}
void list_reverse() //使链表反序（主题）
{
printf("^^after reversing:\n");
if(head == NULL || head->next==NULL) return ;//如果head为空，则返回
list_node *p,*q;
q=head;
p=head->next;
while(p!=NULL)
{
head->next=p->next; //将头指针的next指向p的下一个节点
p->next=q; //将p的next值反指向它的前一个节点q
q=p; //q移向p的位置
p=head->next; //p移向它的下一个位置
}
head = q;
#ifdef TEST
p=head;
while(p!=NULL) //打印该链表
{
printf("%d",p->data);
p=p->next;
}
printf("\n");
#endif
}
void list_destroy() //销毁函数
{
list_node *pmove=NULL,*pdel=NULL;
pmove=head;
while(pmove!=head)
{
pdel=pmove;
free(pdel);
pmove=pmove->next;
}
}
int main()
{
list_create(); //构建单链表
list_reverse(); //反转链表
list_destroy(); //销毁链表
return 0;
}

题：求随机数构成的数组中找到长度大于=3的最长的等差数列

输出等差数列由小到大:

如果没有符合条件的就输出[0,0]

格式：

输入[1,3,0,5,-1,6]

输出[-1,1,3,5]

要求时间复杂度，空间复杂度尽量小

分析：基本算法思路（采用动态规划思想）：首先，只要得到数列的公差和一个首项就可以确定一个等差数列，因此我们要寻找最长等差数列的公差以及首项。其次，为了方便查找公差和首项，我们应该将原数组进行由小到大排序，这样各两数之间的公差也是成递增形势的，这样我们就可以避免回溯查找首项。

因此，在搜寻公差及首项的过程中，我们可以分两三个决策阶段：

1、如果公差为0，应该做何处理。

2、如果公差不为0，应该做何处理。

3、如果找到的数列长度是当前最长的做相应的处理

针对以上情况，我们应该选择一种合适的数据结构——平衡排序树，stl中的set，map，mutiset，multimap是以红黑树结构为形势的容器，无疑是非常合适的，根据题目情况，可能存在具有相同元素的数组，因此我们选择multiset，这样无论我们对数据进行插入排序，查找都是比较高效的，因此总体上是可以满意的。

最后有几项时间上的优化不在这里说明，详情可看代码。若有不足之处，望能不吝指出！^_^

我的实现代码：

[cpp] view plaincopy

/**
Author:花心龟
Blog：http://blog.csdn.net/zhanxinhang
**/
#include <iostream>
#include <ctime>
#include <set>
using namespace std;
void show_longest_seq(const multiset<int>& myset)
{
int maxLength = 0, curr_pos = 0, curr_d = 0, counter=0,i=0; //一些辅助变量
int d_result, a1_result; //存储最长等差数列的公差以及首项
multiset<int>::const_iterator set_it1,set_it2;
/*
(主题)寻找长度最长的等差数列,最坏情况下时间复杂度为O(n^3)
*/
for(set_it1 = myset.begin(); set_it1 != myset.end();)
{
for(set_it2=set_it1,set_it2++; set_it2 != myset.end();)//第二层循环从set_it1所指的下一个元素开始遍历
{
curr_d = *set_it2 - *set_it1; //算得当前公差，注意由于set为自排序容器，从小到大排列，所以curr_d恒为正
if(curr_d == 0) // 如果公差为0
{
counter = myset.count(*set_it1);
set_it2 = myset.upper_bound(*set_it1);//(优化项)跳过与set_it1相等的元素
}
else
{
counter = 2; //（优化项）最小长度要求要不小于所以直接从开始累加
while(myset.find(*set_it1 + counter*curr_d) != myset.end()) //计算数列项个数
++counter;
set_it2 = myset.upper_bound(*set_it2);// （优化项）跳过与*set_it2相等的元素
}
if(counter > maxLength) //如果新数列长度大于maxLength
{
d_result = curr_d;
a1_result = *set_it1;
maxLength = counter;
}
}
curr_pos += myset.count(*set_it1); //计算第一层循环遍历到的当前位置
if(myset.size()-curr_pos < maxLength) // (优化项)如果集合中剩下的元素小于最大数列长度，就退出循环
break;
set_it1 = myset.upper_bound(*set_it1); //下一次set_it1 的位置，并跳过相同元素
}
/*
打印最长等差数列
*/
if(maxLength <= 2)
{
cout<<"longest_seq：[0,0]"<<endl;
}
else
{
cout<<"longest_seq：";
for(i = 0; i<maxLength; i++)
cout<<*(myset.find(a1_result + i*d_result))<<' ';
cout<<endl;
}
}
//Blog：http://blog.csdn.net/zhanxinhang
test in main
int main()
{
int a[]={1,3,0,5,-1,6};
multiset<int> myset;
myset.insert(a,a+6);
show_longest_seq(myset);
cout<<endl;
int l;
srand((unsigned)time(NULL));
for(int j = 0; j < 5; j++)
{
myset.clear();
cout<<"input:[ ";
l=rand()%10;
for(int i = 0; i < l; ++i)
{
int element = rand()%10;
myset.insert(element);
cout<<element<<' ';
}
cout<<']'<<endl;
show_longest_seq(myset);
cout<<endl;
}
return 0;
}

附一张测试结果图：

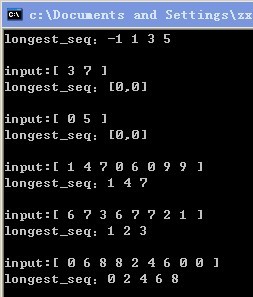
题：两个链表，一升一降。合并为一个升序链表。

分析：（假设升序的链表为链表1，降序的链表为链表2，p1，p2分别作为它们的迭代器，还有一个合并链表用于存放合并后的数据）

法一、最容易想到的且容易实现的就是使两个表都变成升序，然后就是经典的合并排序算法的步骤了，步骤是构建p1，p2两个迭代器，分别用于迭代两个链表，每次遍历，若p1所指的节点数据大于p2所指的节点数据则将p1所指的节点数据插入到要合并链表中去且使p1指向下一个节点，否则将p2将所指的节点数据插入到合并链表中去且使p2指向下一个节点，直到p1和p2任意一个指向了NULL为止。最后可能两个链表中尚有剩余的节点，将其逐个插入到合并链表中去即可。

法二、使用递归方法后序遍历降序链表2，遍历顺序就相当于升序的顺序了。在递归遍历链表2的过程中，需要处理有以下三件事：(注意顺序)

(1) 如果p2的数据小于p1的就插入到合并链表中

(2) 如果p2的数据大于p1，那么就对链表1循环遍历，每次将p1中的数据插到合并链表中，直到p2不大于p1，且p1不为空

(3) 如果p1为空，就直接将p2插入到合并链表中

(这个方法你想到了没！)

完整实现代码：

[cpp] view plaincopy

/**
Author:花心龟
Blog：http://blog.csdn.net/zhanxinhang
**/
#include <stdio.h>
#include <malloc.h>
#include <stdlib.h>
typedef struct list_node
{
int data;
struct list_node * next;
}list_node;
list_node *list1=NULL; //链表头结点
list_node *list2=NULL; //链表头结点
void list_print(const list_node *p)//打印该链表函数
{
if(p==NULL)return;
while(p!=NULL)
{
printf("%d ",p->data);
p=p->next;
}
printf("\n");
}
void list_create(list_node* &head, int data[], int N)
{
if(data == NULL) return;
int i;
list_node *p;
p = (list_node*)malloc(sizeof(list_node));
p->data = data[0];
p->next = NULL;
head = p;
for(i=1;i<N; i++)
{
p->next = (list_node*)malloc(sizeof(list_node));
p->next->data = data[i];
p->next->next = NULL;
p=p->next;
}
}
void list_reverse(list_node* &head) //使链表反序
{
if(head == NULL) return ;//如果head1为空，则返回
list_node *p,*q;
q=head;
p=head->next;
while(p!=NULL)
{
head->next=p->next; //将头指针的next指向p的下一个节点
p->next=q; //将p的next值反指向它的前一个节点q
q=p; //q移向p的位置
p=head->next; //p移向它的下一个位置
}
head = q;
}
void list_destroy(list_node *head) //销毁函数
{
list_node *pmove=NULL,*pdel=NULL;
pmove=head;
while(pmove!=head)
{
pdel=pmove;
free(pdel);
pmove=pmove->next;
}
}
list_node* merge_two_list() //合并链表1和链表2（法一）
{
list_reverse(list2); //反转链表使之与链表一样升序排列
list_node *list_merged; //和并后的链表
list_node *p1,*p2,*p0;
list_merged = (list_node*)malloc(sizeof(list_node));
list_merged->data = 0;
list_merged->next = NULL;
p0 = list_merged;
p1=list1;
p2=list2;
while(p1!=NULL && p2!=NULL)
{
if(p1->data < p2->data)
{
p0->next=(list_node*)malloc(sizeof(list_node));
p0->next->data=p1->data;
p0->next->next=NULL;
p0=p0->next;
p1=p1->next;
}
else
{
p0->next=(list_node*)malloc(sizeof(list_node));
p0->next->data=p2->data;
p0->next->next=NULL;
p0=p0->next;
p2=p2->next;
}
}
while(p1!=NULL)
{
p0->next=(list_node*)malloc(sizeof(list_node));
p0->next->data=p1->data;
p0->next->next=NULL;
p0=p0->next;
p1=p1->next;
}
while(p2!=NULL)
{
p0->next=(list_node*)malloc(sizeof(list_node));
p0->next->data=p2->data;
p0->next->next=NULL;
p0=p0->next;
p2=p2->next;
}
return list_merged;
}
list_node* p0=(list_node*)malloc(sizeof(list_node));
list_node* phead=p0;
list_node* &p1=list1; //p1与list1绑定
list_node* foreach(list_node* p2) //递归合并（法二）
{
if(p2==NULL) return phead;
foreach(p2->next);
if(p1->data > p2->data)
{
p0->next = (list_node*)malloc(sizeof(list_node));
p0->next->data = p2->data;
p0->next->next = NULL;
p0=p0->next;
return phead;
}
while(p1!=NULL && p1->data<=p2->data)
{
p0->next = (list_node*)malloc(sizeof(list_node));
p0->next->data = p1->data;
p0->next->next = NULL;
p0=p0->next;
p1 = p1->next;
}
if(p1==NULL)
{
p0->next = (list_node*)malloc(sizeof(list_node));
p0->next->data = p2->data;
p0->next->next = NULL;
p0=p0->next;
}
return phead;
}
//Blog：http://blog.csdn.net/zhanxinhang
int main()
{
int list1_data[] = {1,4,6,8,10}; //链表数据升序可在这里该数据进行测试
int list2_data[] = {14,9,3,2}; //链表数据降序
list_create(list1,list1_data,5); //构建单链表
list_create(list2,list2_data,4); //构建单链表
list_print(list1);
list_print(list2);
//list_node *list_merged=merge_two_list(); //合并两个链表
//list_print(list_merged->next); //打印合并后的链表
list_node *list_merged2=foreach(list2); //使用递归合并两个链表
list_print(list_merged2->next);
list_destroy(list1); //销毁链表
list_destroy(list2); //销毁链表
// list_destroy(list_merged); //销毁合并后的链表
list_destroy(list_merged2); //销毁合并后的链表
system("pause");
return 0;
}

题：如何删除链表的倒数第m的元素？

分析：构建p0,p1两个迭代器，初始使p0和p1指向头结点，接着使p1移动到第m+1项，然后指向头得p0与p1同时前进，当p1指向空节点的时候结束，这时p0所指的位置就是倒数第m个，时间复杂度为O（n）

实现代码：（为了学习的需要，现在C++朋友采用c++实现，不能满足c朋友要采用c实现的愿望，此实为c++朋友的遗憾，不过一切重在思想。^_^）

[cpp] view plaincopy

/**
Author:花心龟
Blog：http://blog.csdn.net/zhanxinhang
**/
#include <iostream>
#include <list>
using namespace std;
class App
{
list<int> *plist;
void delete_node_at_last(int m) //today`s topic
{
list<int>::iterator p0, p1;
p0=p1=p2=plist->begin();
//使p1移到第m+1项
for(int i=1; i<=m; i++)
p1++;
//p0和p1同时前进，当p1到达终点时p0所指向的就是倒数第m个节点
while(p1!=plist->end())
p0++,p1++;
//删除节点
plist->erase(p0);
}
void create_list()
{
int list_data[]={1,2,3,4,5,6,7,8,9}; //链表数据
plist = new list<int>(list_data, list_data+sizeof(list_data)/sizeof(int));
}
void print_list()
{
list<int>::iterator it;
for(it=plist->begin(); it!=plist->end(); it++)
cout<<*it<<' ';
}
public:
//test in run funtion
void run()
{
create_list();
delete_node_at_last(3); //删除倒数第三个节点
print_list();
}
~App()
{
delete plist;
}
};
//Blog：http://blog.csdn.net/zhanxinhang
int main()
{
App myapp;
myapp.run();
system("pause");
return 0;
}

题：1、如何判断一个字符串是对称的？如a，aa，aba。

2、如何利用2函数找出一个字符串中的所有对称子串？

分析：

且看第一个问题判断字符串对称，有以下两种方法。

方法一、使迭代器p1指向头，p2指向尾。使p1，p2相对而行(—> | <—)，每次比较p1，p2是否相等，直到它们相遇。

方法二、使p1、p2指向中间的一个元素（如果字符串长度为偶数的话就指向中间两个相邻的元素），使它们相向而行(<— |—>)，每次比较p1，p2是否相等。直到它们一个指向头一个指向尾便结束。

（可以看出方法1明显好于方法2）

现在看第二个问题打印所有的对称子串，判断对称子串的问题我们似乎已经解决，且有以上两种方法，针对现在的情况是否两种都合适呢，确切的说不是。如果是方法一，请想象一下，如果要p1，p2一个指向子串的头一个指向子串的尾，那么至少要两层循环一层控制p1一层控制p2，还有一层循环用于判断子串是否对称，也就是说总共需要三层嵌套循环，时间复杂度指数为3。而如果选择方法二呢？两层循环就能实现，不过要适应现在这种情况需要做些修改，就是针对偶数长度的子串进行一次遍历，再针对奇数长度的子串进行一次遍历，也就是两层嵌套循环中内层有两次循环，时间复杂度指数为2。详情且看代码。

实现加测试代码：

[cpp] view plaincopy

/**
Author:花心龟
Blog：http://blog.csdn.net/zhanxinhang
**/
#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
class App
{
typedef string::iterator Iter_t;
string m_str;
void print(Iter_t p1, Iter_t p2) //打印从p1开始到p2结束的字符
{
while(p1<=p2)
{
cout<<*p1;
p1++;
}
cout<<" | ";
}
bool isHuiwen1(Iter_t start,Iter_t end) //法1判断是否为对称子串
{
Iter_t p1 = start;
Iter_t p2 = end;
int times = (distance(p1,p2)+1) / 2; //比较次数
while(times)
{
if(*p1 != *p2)
return false;
p1++;
p2--;
times--;
}
return true;
}
bool isHuiwen2(Iter_t mid_it) //法2判断是否为对称子串
{
Iter_t p1,p2;
p1 = p2 = mid_it;
while(p1>=m_str.begin() && p2 < m_str.end())
{
if(*p1 != *p2)
break;
print(p1,p2);//打印从p1到p2的字符
p1--,p2++;
}
p1 = p2 = mid_it;
p2++; //使p2向前移动一个位置，此时p1，p2分别指向中间两个相邻位置
while(p1>=m_str.begin() && p2 < m_str.end())
{
if(*p1 != *p2)
return false;
print(p1,p2);//打印从p1到p2的字符
p1--,p2++;
}
return true;
}
void show_all_substr_of_huiwen1() //法一打印所有对称子串
{
Iter_t p2=m_str.end()-1;
Iter_t p1 = m_str.begin();
for(;p1!=m_str.end();p1++)
for(p2=p1;p2!=m_str.end();p2++)
{
if(isHuiwen1(p1,p2))
print(p1,p2);
}
}
void show_all_substr_of_huiwen2() //法二打印所有对称子串
{
Iter_t it = m_str.begin();
for(;it!=m_str.end();it++)
{
isHuiwen2(it);
}
}
public:
void run()
{
m_str="abaaba";
cout<<"测试数据为:abaaba"<<endl;
show_all_substr_of_huiwen1();
cout<<endl;
show_all_substr_of_huiwen2();
cout<<endl;
m_str="asdfie";
cout<<"测试数据为:asdfie"<<endl;
show_all_substr_of_huiwen1();
cout<<endl;
show_all_substr_of_huiwen2();
cout<<endl;
m_str="aabaa";
cout<<"测试数据为:aabaa"<<endl;
show_all_substr_of_huiwen1();
cout<<endl;
show_all_substr_of_huiwen2();
cout<<endl;
//时间比较//
m_str="this is a string for testing. aabaa alskjdfkljasdjflasdflkajsldkjfsjlakjsdlfjwoekjlakjlsdkjflsajlkdjfowieuoriuq aaddbb sldjfalkjsdlfkjasldjflajsldfjalskdjflakjsdlfkjaslkdjflajsdlfkjaslkdjflkajsdlkjflkasjdlfjaklsjdkfljaklsdjfklsajdflkjslkdjflaskjdlfkjalsdjlfkajsldfkjlaksjdfljasldjflaskjdfkasjdflaksjdkfljaskldfjlaksjdfljasldjflaksjdkljfkalsjdlkfjasldjflasjdlfjasldjfklsajdfljaskldfjlsakjdflkasjdfkl this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.make -k make -k make -k make -k make -k make -k is is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.make -k make -k make -k make -k make -k make -k is is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.make -k make -k make -k make -k make -k make -k is is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.make -k make -k make -k make -k make -k make -k is is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.make -k make -k make -k make -k make -k make -k is is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.make -k make -k make -k make -k make -k make -k is is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.make -k make -k make -k make -k make -k make -k is is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.make -k make -k make -k make -k make -k make -k is is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.make -k make -k make -k make -k make -k make -k is is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.make -k make -k make -k make -k make -k make -k is is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.make -k make -k make -k make -k make -k make -k is is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.this is a string for testing.make -k make -k make -k make -k make -k make -k end";
time_t start,record1;
cout<<"show all substr of huiwen 1:";
system("pause");
start = time(NULL);
show_all_substr_of_huiwen1();
record1 = time(NULL);
cout<<endl;
cout<<"time:"<<record1-start;
cout<<endl;
cout<<"show all substr of huiwen 2:";
system("pause");
start = time(NULL);
show_all_substr_of_huiwen2();
record1 = time(NULL);
cout<<endl;
cout<<"time:"<<record1-start;
cout<<endl;
cout<<"(可以看到打印速度明显快于上一次)";
}
};
int main()
{
App myapp;
myapp.run();
system("pause");
return 0;
}

测试结果：

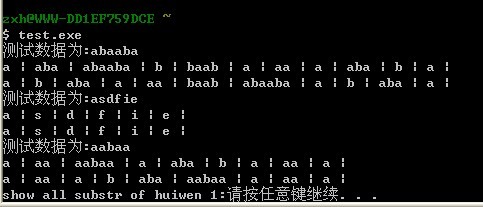
各测试数据下的一二行为打印出来的所有对称字串。

按下任意键后：

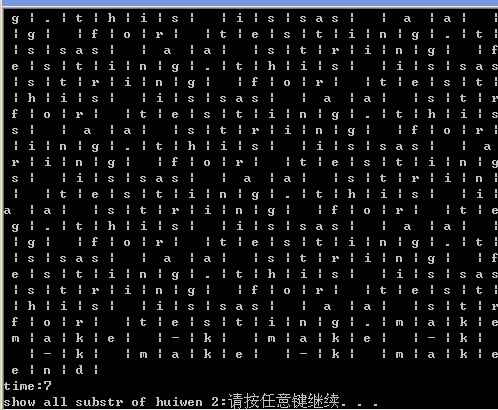
以上是使用方法1打印出来的结果。

按下任意键后：

以上便是用方法2打印出来的结果。

题：假设你有一个用1001个整数组成的数组，这些整数是任意排列的，但是你知道所有的整数都在1到1000(包括1000)之间。此外，除一个数字出现两次外，其他所有数字只出现一次。假设你只能对这个数组做一次处理，用一种算法找出重复的那个数字。如果你在运算中使用了辅助的存储方式，那么你能找到不用这种方式的算法吗?

分析：

方法一、若使用辅助的存储方式，该选择何种存储方式呢？可使用hash的存储方式，以1到1000作为hash表的索引，遍历原数组，统计各数字出现的个数并存储到以该数字为索引值的hash表中，若某个hash[x]的值为2则退出循环，x就是重复出现两次的数字。时间复杂度最坏是O(n)。优点：高效率，缺点：消耗的内存空间过大。代码如下：

[cpp] view plaincopy

int fun1(const int a[])
{
int hash[1002]={0};
int x=0;
for(int i = 0; i<1001; i++)
{
if((++hash[a[i]]) == 2)
{
x = a[i];
break;
}
}
return x;
}

方法二、若不使用辅助的存储方式呢？已知1001个整数组成的数组只有一个数字出现了两次，且整数都在1到1000之间，所以可推得数组里面包含了1到1000之间的所有数字为[1,2,3……1000]和一个出现两次的x为1到1000中的任一个数字。这样就可以计算原数组里的所有数字之和S1和等差数列[1,2,3……1000]的和S2，再计算S1与S2之差，该差就是原数组中出现两次的数字x。时间复杂度是固定的O(n)。优缺点：内存空间消耗几乎没有，但是效率要输于使用hash表的存储方式。代码如下：

[cpp] view plaincopy