关于JavaScript的数组随机排序

昨天了解了一下Fisher–Yates shuffle费雪耶兹随机置乱算法，现在再来看看下面这个曾经网上常见的一个写法：

function shuffle(arr) { arr.sort(function () { return Math.random() - 0.5; }); 
}

或者使用更简洁的 ES6 的写法：

function shuffle(arr) { arr.sort(() => Math.random() - 0.5); }

但是这种写法是有问题的，它并不能真正地随机打乱数组。

问题

看下面的代码，我们生成一个长度为 10 的数组['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j']，使用上面的方法将数组乱序，执行多次后，会发现每个元素仍然有很大机率在它原来的位置附近出现。

let n = 10000; let count = (new Array(10)).fill(0); for (let i = 0; i < n; i ++) { let arr = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j']; arr.sort(() => Math.random() - 0.5); count[arr.indexOf('a')]++; } console.log(count);

在浏览器控制台中执行，输出[ 2891, 2928, 1927, 1125, 579, 270, 151, 76, 34, 19 ](带有一定随机性，每次结果都不同，但大致分布应该一致)，即进行 10000 次排序后，字母'a'(数组中的第一个元素)有约 2891 次出现在第一个位置、2928 次出现在第二个位置，与之对应的只有 19 次出现在最后一个位置。如果把这个分布绘制成图像，会是下面这样：

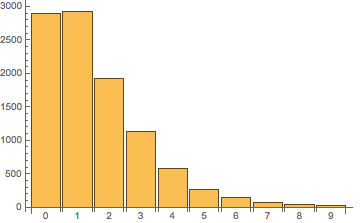
类似地，我们可以算出字母'f'(数组中的第六个元素)在各个位置出现的分布为[ 312, 294, 579, 1012, 1781, 2232, 1758, 1129, 586, 317 ]，图像如下：

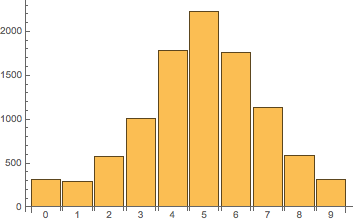
如果排序真的是随机的，那么每个元素在每个位置出现的概率都应该一样，实验结果各个位置的数字应该很接近，而不应像现在这样明显地集中在原来位置附近。因此，我们可以认为，使用形如arr.sort(() => Math.random() - 0.5)这样的方法得到的并不是真正的随机排序。

另外，需要注意的是上面的分布仅适用于数组长度不超过 10 的情况，如果数组更长，比如长度为 11，则会是另一种分布。比如：

function newarr(){
let a = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k']; // 长度为11
let n = 10000; 
var count = (new Array(a.length)).fill(0); 
for (var i = 0; i < n; i ++) { var arr = [].concat(a); arr.sort(() => Math.random() - 0.5); count[arr.indexOf('a')]++; 
} 
//console.log(count);
return count;
}newarr();

在浏览器控制台中多次执行，其中第一个元素'a'的分布位置结果如下：

(11) [785, 826, 629, 652, 937, 1079, 960, 680, 617, 986, 1849]
newarr()
(11) [844, 816, 636, 665, 947, 1053, 901, 654, 661, 982, 1841]
newarr()
(11) [804, 829, 622, 655, 923, 1093, 916, 667, 591, 974, 1926]
newarr()
(11) [779, 793, 655, 713, 916, 1161, 911, 642, 579, 936, 1915]
newarr()
(11) [786, 783, 607, 653, 956, 1116, 954, 655, 619, 1028, 1843]
newarr()
(11) [867, 797, 647, 635, 943, 1056, 929, 652, 572, 977, 1925]

虽然数组长度大于10后比之前的分布更均匀，但是明显还有问题（最后一个最大）。

分布不同的原因是 v8 引擎中针对短数组和长数组使用了不同的排序方法(下面会讲)。可以看到，两种算法的结果虽然不同，但都明显不够均匀。

探索

看了一下ECMAScript中关于Array.prototype.sort(comparefn)的标准，其中并没有规定具体的实现算法，但是提到一点：

Calling comparefn(a,b) always returns the same value v when given a specific pair of values a and b as its two arguments.

也就是说，对同一组a、b的值，comparefn(a, b)需要总是返回相同的值。而上面的() => Math.random() - 0.5(即(a, b) => Math.random() - 0.5)显然不满足这个条件。

翻看v8引擎数组部分的源码，注意到它出于对性能的考虑，对短数组使用的是插入排序，对长数组则使用了快速排序，至此，也就能理解为什么() => Math.random() - 0.5并不能真正随机打乱数组排序了。(有一个没明白的地方：源码中说的是对长度小于等于 22 的使用插入排序，大于 22 的使用快排，但实际测试结果显示分界长度是 10。)

解决方案

知道问题所在，解决方案也就比较简单了。

方案一

既然(a, b) => Math.random() - 0.5的问题是不能保证针对同一组a、b每次返回的值相同，那么我们不妨将数组元素改造一下，比如将每个元素i改造为：

let new_i = { v: i, r: Math.random() };

即将它改造为一个对象，原来的值存储在键v中，同时给它增加一个键r，值为一个随机数，然后排序时比较这个随机数：

arr.sort((a, b) => a.r - b.r);

完整代码如下：

function shuffle(arr) { let new_arr = arr.map(i => ({v: i, r: Math.random()})); new_arr.sort((a, b) => a.r - b.r); arr.splice(0, arr.length, ...new_arr.map(i => i.v)); } let a = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j']; let n = 10000; let count = (new Array(a.length)).fill(0); for (let i = 0; i < n; i ++) { shuffle(a); count[a.indexOf('a')]++; } console.log(count);

一次执行结果为：[ 1023, 991, 1007, 967, 990, 1032, 968, 1061, 990, 971 ]。多次验证，同时在这儿查看shuffle(arr)函数结果的可视化分布，可以看到，这个方法可以认为足够随机了。

方案二(Fisher–Yates shuffle)

需要注意的是，上面的方法虽然满足随机性要求了，但在性能上并不是很好，需要遍历几次数组，还要对数组进行splice等操作。

考察Lodash 库中的 shuffle 算法，注意到它使用的实际上是Fisher–Yates 洗牌算法，这个算法由 Ronald Fisher 和 Frank Yates 于 1938 年提出，然后在 1964 年由 Richard Durstenfeld 改编为适用于电脑编程的版本。

function shuffle(arr) { var i = arr.length, t, j; while (i) { j = Math.floor(Math.random() * i--); t = arr[i]; arr[i] = arr[j]; arr[j] = t; } } //对应的ES6如下
function shuffle(arr) { let i = arr.length; while (i) { let j = Math.floor(Math.random() * i--);  //5555
 [arr[j], arr[i]] = [arr[i], arr[j]]; } }