大家好,我是爱讲故事的某某某。 欢迎来到今天的【五分钟机器学习】专栏内容 --《向量支持机SVM》 今天的内容将详细介绍SVM这个算法的训练过程以及他的主要优缺点,还没有看过的小伙伴欢迎去补番:
【五分钟机器学习】向量支持机SVM——学霸中的战斗机
在视频的内容中,我们介绍了SVM的主要思想及Hard Margin SVM的优化过程。
在今天的专栏中,我们将填上视频中的坑,本期专栏的主要内容有两块:
- 推导Hard Margin SVM两个Margin Boundary之间的距离
- Soft-Margin SVM 的逻辑思路介绍
推导Hard Margin SVM两个Margin Boundary之间的距离
我们假定一个Hard Margin SVM如下图所示。
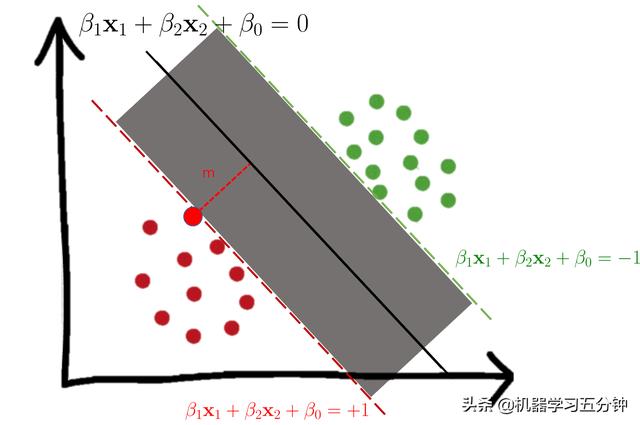
Fig1. Hard-Margin SVM实例
其中,决策分界面Decision Boundary的公式:
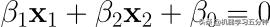
Eq1. Decision Boundary
两个边界分界面Margin Boundary的公式:
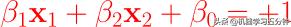
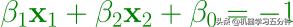
Eq2. Margin Boundary
我们假定图1中高光的点(
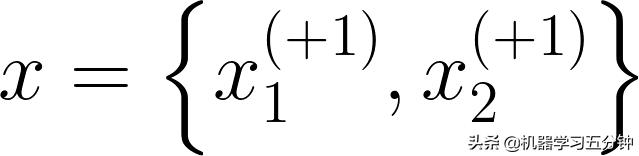
)在边界分界面上面,即满足Eq2中的条件b1x1+b2x2+b0 = +1(落在红色的线上面)。那么根据点到直线的公式:
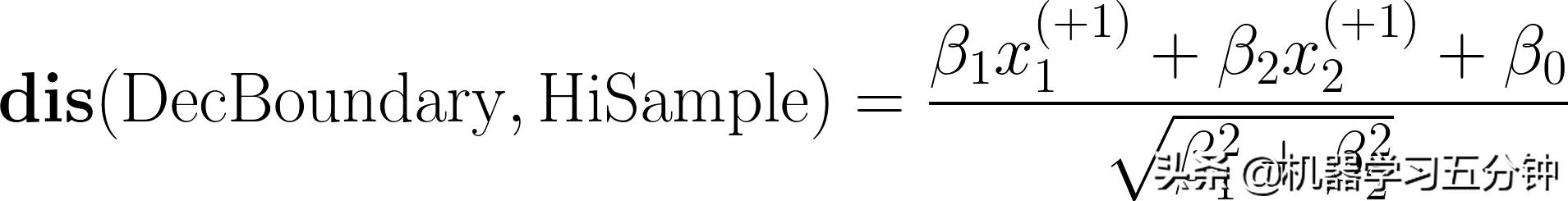
Eq3. 高光点HiSample到决策分界面DecBoundary的距离
根据定义:
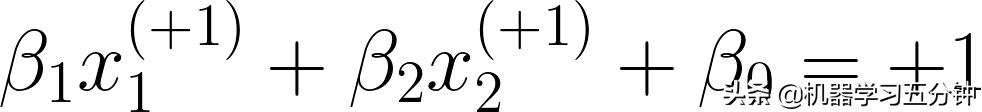
所以Eq3可以写成:
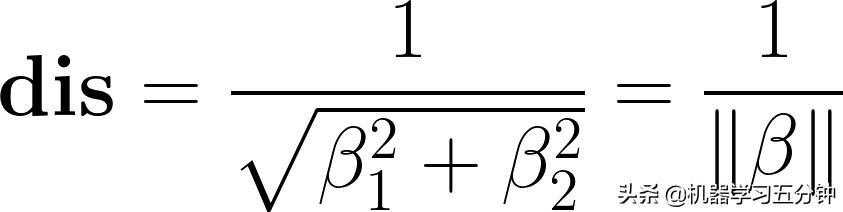
Eq4. 高光点到决策分界面的距离
因为决策分界面正好在两个边界分界面的正中间,即两个类别之间的间距为:
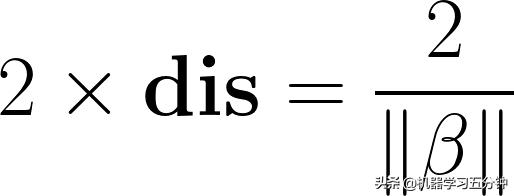
Eq5. 两个边界分界面之间的距离,即HardMargin
以上就是Hard-Margin SVM的两个边界分界面之间的距离的推导过程。
Soft-Margin SVM 的逻辑思路介绍
Soft-Margin SVM要解决的问题有两个:
- 和Hard-MarginSVM一样,需要最大化间距
- 在保证大局的正确性的同时,引入容错率这个概念
对于第一点,如果你还记得我们的做法是将距离公式,转化为Hard-margin SVM的Loss function。使其在最小化Loss的同时,也可以最大化Margin,即:
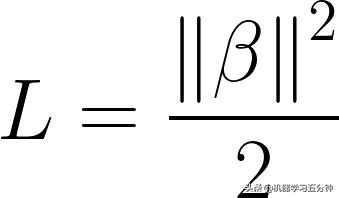
Eq6. Hard Margin SVM的Loss
在这个基础上,我们引入Hinge Loss作为允许部分错误分类的过程。所以我们Soft-Margin SVM的Loss可以写成:
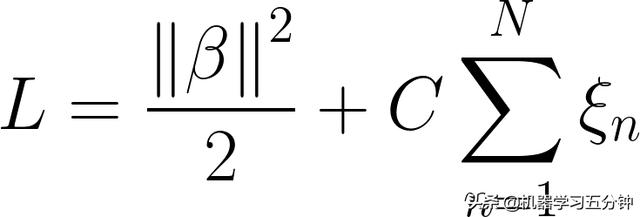
Eq7. Soft Margin SVM的Loss
其中N表示样本数量,C表示惩罚系数(Penalty Term),而Hinge loss 的部分为:
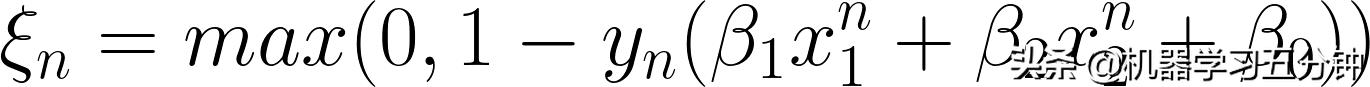
Eq8. Hinge Loss 的定义
【重点】这里我们不妨仔细看下这个公式,他的逻辑分两层,从内到外看:
- 对于下面的部分,他的计算结果表示错误分类的误差和
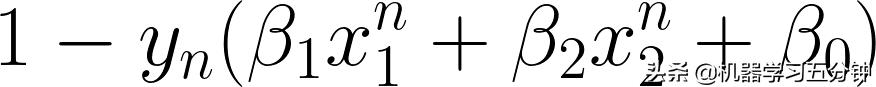
Eq9. Hinge Loss 的定义(2)
比如,当你y_n=1,并且b1x1+b2x2+b0=1时,表示通过分类器得到的结果和样本真是标记相同,这个式子的输出为0;反之,当你y_n=1,并且b1x1+b2x2+b0=-1时,表示通过分类器得到的结果和样本真是标记相反,这个式子的输出为2,表示为有误差。
- max(0, ....) 这部分表示为取上面步骤的误差计算结果和0这两个数值中大的数值作为输出。
比如,如果SVM的分类结果没错,上面步骤的输出应该是0,那么max(0,0)=0;
如果SVM的分类结果有误,上面步骤的输出应该大于0(比如2),那么max(0,2)=2;
【重点】所以通过这个部分,你可以看到优化Soft Margin SVM Loss的过程就是在平衡两个点:1. 最大化间距(Hard SVM), 还是2. 允许部分误差(Hinge Loss)。而为了更好的平衡这两点,我们引入了惩罚因子C。当C变大时,意味着我们会更多的惩罚Hinge Loss,即尽可能少犯错;当C变小时,意味着我们会尽可能惩罚Hard SVM,也就是Margin更大。
为了更好的理解,这里给你准备了一个例子,对比下Hard Margin SVM和Soft Margin SVM。可以看到Soft margin SVM 由于Hinge Loss的引入,增加了很多容错率,从而保证大局上的正确率。
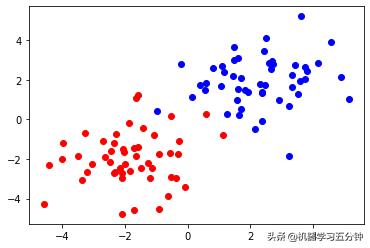
Fig2. Toy Dataset example
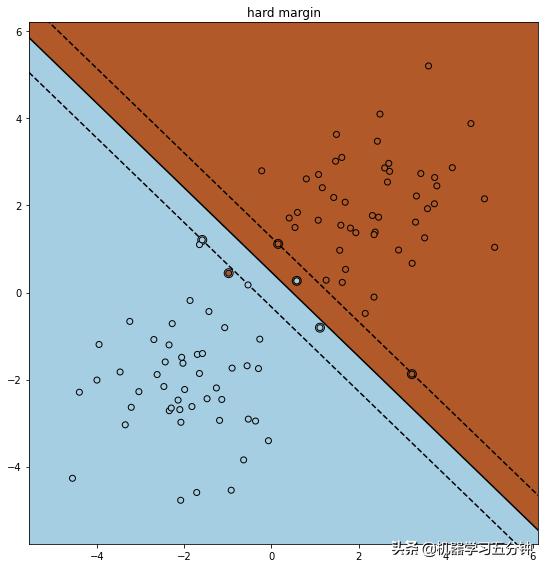
Fig3. Hard Margin SVM 分类结果
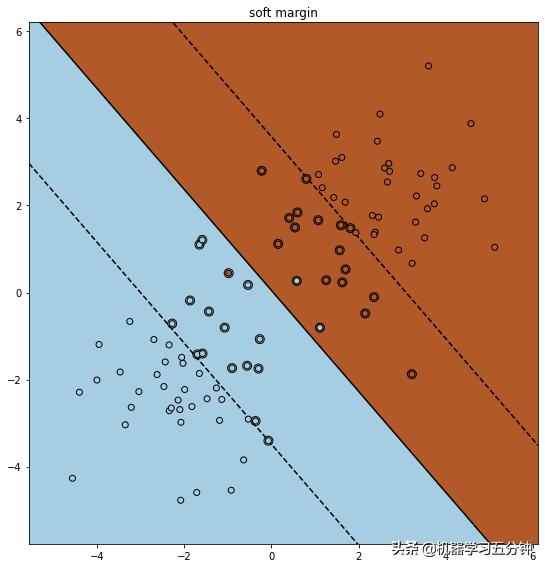
Fig4. Soft Margin SVM分类结果
以上就是今天的【五分钟机器学习】SVM篇的主要内容了。
如果你觉得本期内容有所帮助,欢迎素质三连。
您的支持将是我继续发电的最大动力~
我是某某某







)











)
