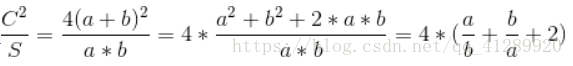题干:
福克斯在玩一款手机解迷游戏,这个游戏叫做”两点”。基础级别的时候是在一个n×m单元上玩的。像这样:
每一个单元有包含一个有色点。我们将用不同的大写字母来表示不同的颜色。
这个游戏的关键是要找出一个包含同一颜色的环。看上图中4个蓝点,形成了一个环。一般的,我们将一个序列 d1,d2,...,dk 看成一个环,当且仅当它符合下列条件时:
1. 这k个点不一样,即当 i≠j时, di 和 dj不同。
2. k至少是4。
3. 所有的点是同一种颜色。
4. 对于所有的 1≤i≤k-1: di 和 di+1 是相邻的。还有 dk 和 d1 也应该相邻。单元 x 和单元 y 是相邻的当且仅当他们有公共边。
当给出一幅格点时,请确定里面是否有环。
Input
单组测试数据。
第一行包含两个整数n和m (2≤n,m≤50):板子的行和列。
接下来n行,每行包含一个有m个字母的串,表示当前行每一个点的颜色。每一个字母都是大写字母。
Output
如果有环输出Yes,否则输出No。
Sample Input
3 4
AAAA
ABCA
AAAA
3 4
AAAA
ABCA
AADASample Output
Yes
No解题报告:
数据水啊,纯暴力都能过。
这题其实dfs中的状态,加一个前驱的记录,就不需要step了,这样可以优化时间了。因为我们可以先跑并查集,然后一个集合一个集合的搜,如果搜到以前搜过的点,那就return 1;。
这样好处是,不需要一个一个点的搜索了,另外,这题vis数组是不需要回溯的。
另外,算是个dfs(换句话来说,是搜索的)的共同坑点吧,那就是对起点的标记,因为经常在起点那里就落下一个状态,,,比如【51Nod - 1268】和为K的组合 (背包 或 dfs)这题。
AC代码:
#include<bits/stdc++.h>using namespace std;
int n,m;
int nx[4] = {0,1,0,-1};
int ny[4] = {1,0,-1,0};
bool vis[55][55];
char maze[55][55];
bool ok(int x,int y) {if(x <= n && x >= 1 && y <= m && y >= 1) return 1;return 0;
}
bool dfs(int idx,int idy,char tar,int x,int y,int step) {if(x == idx && y == idy && step >=3 ) {return 1;}for(int k = 0; k<4; k++) {int tx = x+nx[k];int ty = y+ny[k];if(ok(tx,ty) && maze[tx][ty] == tar && vis[tx][ty] == 0) {vis[tx][ty]=1;if(dfs(idx,idy,tar,tx,ty,step+1)) return 1;}}return 0 ;}
int main()
{while(~scanf("%d%d",&n,&m)) {int flag = 0;memset(vis,0,sizeof vis);for(int i = 1; i<=n; i++) {scanf("%s",maze[i]+1);}for(int i = 1; i<=n; i++) {for(int j = 1; j<=m; j++) {for(int k = 0; k<4; k++) {if(maze[i+nx[k]][j+ny[k]] != maze[i][j]) continue;memset(vis,0,sizeof vis);vis[i+nx[k]][j+ny[k]]=1;
// vis[i][j]=1;if(dfs(i,j,maze[i][j],i+nx[k],j+ny[k],0)) {flag=1;break;}}if(flag) break;}if(flag) break;}if(flag) puts("Yes");else puts("No");}return 0 ;} 总结:
刚开始还是犯了小错误,三层for那里,最外面两层都写的是<=n....其实内层应该是<=m