---

CheckiO 是面向初学者和高级程序员的编码游戏，使用 Python 和 JavaScript 解决棘手的挑战和有趣的任务，从而提高你的编码技能，本博客主要记录自己用 Python 在闯关时的做题思路和实现代码，同时也学习学习其他大神写的代码。

CheckiO 官网：https://checkio.org/

我的 CheckiO 主页：https://py.checkio.org/user/TRHX/

CheckiO 题解系列专栏：https://itrhx.blog.csdn.net/category_9536424.html

CheckiO 所有题解源代码：https://github.com/TRHX/Python-CheckiO-Exercise

---

题目描述

【Largest Rectangle in a Histogram】：求直方图最大矩阵面积，给定一个列表，列表中的元素表示一个直方图中所有矩形的高度，计算在直方图内构建的最大矩形的面积。

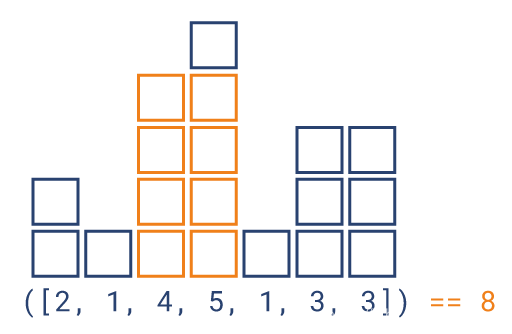
【链接】：https://py.checkio.org/mission/largest-histogram/

【输入】：直方图中所有矩形的高度列表

【输出】：最大矩形的面积

【前提】：0 < len(data) < 1000

【范例】：

largest_histogram([5]) == 5
largest_histogram([5, 3]) == 6
largest_histogram([1, 1, 4, 1]) == 4
largest_histogram([1, 1, 3, 1]) == 4
largest_histogram([2, 1, 4, 5, 1, 3, 3]) == 8

代码实现

def largest_histogram(histogram):i = 0max_value = 0stack = []histogram.append(0)while i < len(histogram):if len(stack) == 0 or histogram[stack[-1]] <= histogram[i]:stack.append(i)i += 1else:now_idx = stack.pop()if len(stack) == 0:max_value = max(max_value,i * histogram[now_idx])else:                    max_value = max(max_value,(i- stack[-1] -1) * histogram[now_idx])return max_valueif __name__ == "__main__":#These "asserts" using only for self-checking and not necessary for auto-testingassert largest_histogram([5]) == 5, "one is always the biggest"assert largest_histogram([5, 3]) == 6, "two are smallest X 2"assert largest_histogram([1, 1, 4, 1]) == 4, "vertical"assert largest_histogram([1, 1, 3, 1]) == 4, "horizontal"assert largest_histogram([2, 1, 4, 5, 1, 3, 3]) == 8, "complex"print("Done! Go check it!")

大神解答

大神解答 NO.1

def largest_histogram(h):result = min(h) * len(h)for w in range(1, len(h)):for i in range(len(h) - w + 1):result = max(result, min(h[i:i + w]) * w)return result

大神解答 NO.2

def largest_histogram(h):n = len(h)return max((j - i) * min(h[i:j]) for i in range(n) for j in range(i+1, n+1))

大神解答 NO.3

def largest_histogram(histogram):return max(height * max(len(strip) for strip in ''.join('x' if x >= height else ' ' for x in histogram).split()) for height in set(histogram))

大神解答 NO.4

def mesure(hist):return min(hist) * len(hist)def sub_histograms(hist):for start in range(len(hist)):for stop in range(start+1, len(hist)+1):yield hist[start:stop]def largest_histogram(histogram):return max(map(mesure, sub_histograms(histogram)))