在学习复数时，最近有个别比较好学的同学提出一个问题：

“对于复数系数一元二次方程，是否可以用求根公式求解呢？”

——回答是肯定的！

关于复数集中解一元二次方程的问题。其实，在复数集内解关于x的一元二次方程ax²+bx+c=0(a≠0)....(*)时,有以下一些重要结论：(其中判别式△=b²-4ac)(1)当a,b,c∈R时,若△＞0,则方程(*)有两个不相等的实数根；(2)若△=0,则方程(*)有两个相等的实数根；(3)若△＜0,则方程(*)有两个复数根 x₁，x_{2 (}x₁，x_{2为共轭复数)。}

      _{(4)当a,b,c不全为实数时,不能用根的判别式△来判断方程(*)是否有实数 根.即当△＞0时方程(*)可能有实数根，也可能没有实数根，可能只有虚数根。同样的，当△＜0时方程(*)可能有实数根，也可能没有实数根，可能只有虚数根。这是非常值得我们引起高度注意的！}

_{(5)当a,b,c都是一般的复数时，上述方程(*)的韦达定理(即根与系数之间的关系)仍然成立。}

     _{如果a,b,c都是一般的复数时，本文现在就来着重研究一下方程(*)的一般求根公式。}

_{总而言之，具体说明如下。}

也就是说，如果x=u+vi(u,v,a,b都是实数)是a+bi的平方根，那么

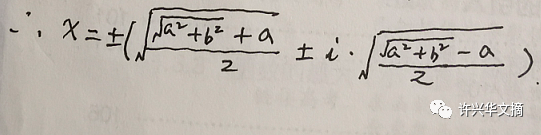
【推荐阅读】

2020届成都市高三理科数学二诊试题及答案

2020届成都市高三文科数学二诊试题及答案

2019年广西高中学业水平考试数学真题与详解

2019年广西普通高中学业水平考试数学模拟试卷(NNSZ版)

高中选修2-2之2.1直接证明与间接证明课件

高中选修2-2直接证明与间接证明的作业详解

用数学归纳法证明代数等式作业详解

高中数学选修2-2数学归纳法2课件

高中数学选修2-2数学归纳法第2课时作业与详解

用数学归纳法证明数学猜想......