离散分布
退化分布
若r.v. 只取常数值c,即 ,这时分布函数为:
把这种分布称为退化分布或者单点分布。
伯努利分布
在一次实验中,事件A出现的概率为 ,不出现的概率为 ,若用 记事件A出现的次数,则 仅取值0或1,相应的概率分布为
这个分布称为伯努利分布,也叫两点分布。
from IPython.core.pylabtools import figsize
import numpy as np
import scipy.stats as stats
from matplotlib import pyplot as plt
import warnings
warnings.filterwarnings("ignore")
%matplotlib inline
X = np.arange(0, 2,1)
p = 0.2
pList = stats.bernoulli.pmf(X, p)
plt.plot(X, pList, marker='o',linestyle='None')
plt.vlines(X, 0, pList)
plt.xlabel('$k$')
plt.ylabel('$P(X = k)$')
plt.title('$P=%.2f$' % p)
plt.show()

二项分布
N:实验次数或潜在事件发生数的一个正整数
P:在一次实验中一种事件发生的概率
figsize(12.5, 4)
binomial = stats.binom
parameters = [(10, .4), (10, .9)]
for i in range(2):
N, p = parameters[i]
_x = np.arange(N + 1)
plt.bar(_x - 0.5, binomial.pmf(_x, N, p),alpha=0.6,
label="$N$: {}, $p$: {:.1f}" .format(N, p),
linewidth=3)
plt.legend(loc="upper left")
plt.xlim(0, 10.5)
plt.xlabel("$k$")
plt.ylabel("$P(X = k)$")
Text(0, 0.5, '$P(X = k)$')

超几何分布
对某批N 件产品进行不放回抽样检查,若这
批产品中有M件次品,现从整批产品中随机抽出
n件产品,则在
这n件产品中出现的次品数x是随机变量,它取值0,1, 2,..
n,其概率分布为超几何分布.
# 超几何分布 hypergeometric(ngood, nbad, nsample, size=None) 好的总数、坏的总数、每次采样数、试验次数
s = np.random.hypergeometric(10,20,5,size=1000000)
p = sum(s>=4)/1000000.
fig = plt.figure(figsize=(8,6))
a1 = fig.add_subplot(2,2,1)
a1.hist(s ,bins=20,color='b',alpha=0.3)
plt.show()

Poisson分布
若事件流具有平稳性、无后效性、普通性,则称该事件流为泊松事件流(泊松流)。
平稳性:在任意时间区间内,事件发生k次(k≥0)的概率只依赖于区间长度而与区间端点无关.
无后效性:在不相重叠的时间段内,事件的发生是相互独立的.
普通性:如果时间区间充分小,事件出现两次或两次以上的概率可忽略不计.
λ为任意正数,被称为Poisson分布的强度。λ越大,得到大值的概率越大;λ越小,得到小值的概率越大。
k为任意非负整数,即k必须为0、1、2之类的值。
Poisson分布的重要性质是:它的期望值和方差值都等于它的参数
figsize(12.5, 4)
lams = [1,5,10]
for i in lams:
plt.scatter(np.arange(20),stats.poisson.pmf(np.arange(20), mu=i),s=100,label='lam={}'.format(i))
plt.plot(np.arange(20),stats.poisson.pmf(np.arange(20), mu=i))
plt.legend()
<matplotlib.legend.Legend at 0x277b1ad2f28>

几何分布
在事件A发生的概率为p的伯努利试验中,若
以η记A首次出现时的试验次数,则η为随机变量,它可能取的
值为1,2,3,…其概率分布为几何分布:
η
k = 5
p = 0.6
X = np.arange(1, k+1,1)
pList = stats.geom.pmf(X,p)
plt.vlines(X, 0, pList,colors='r')
plt.xlabel('$k$')
plt.ylabel('$p\{X=k\}$')
plt.title('p=%.2f' % p)
plt.show()

帕斯卡分布
在伯努利试验中,若以ζ记第r次成
功出现时的试验次数,则ζ是随机变量,取值r,r+l, .其概率
分布为帕斯卡分布: ζ
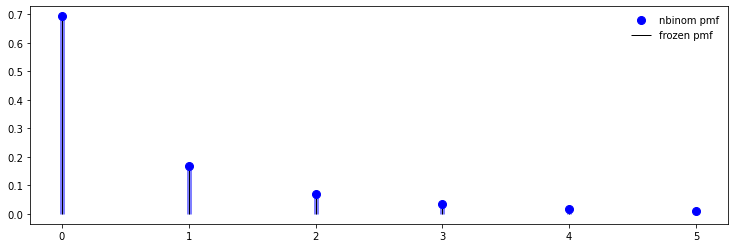
负二项分布
对巴斯卡分布,可以略加推广,即去掉r是正整数的限制,这
便得到负二项分布
对于任意实数r>0,称
为负二项分布。
可证
fig, ax = plt.subplots(1, 1)
n, p = 0.4, 0.4
mean, var, skew, kurt = stats.nbinom.stats(n, p, moments='mvsk')
x = np.arange(stats.nbinom.ppf(0.01, n, p),
stats.nbinom.ppf(0.99, n, p))
ax.plot(x, stats.nbinom.pmf(x, n, p), 'bo', ms=8, label='nbinom pmf')
ax.vlines(x, 0, stats.nbinom.pmf(x, n, p), colors='b', lw=5, alpha=0.5)
rv = stats.nbinom(n, p)
ax.vlines(x, 0, rv.pmf(x), colors='k', linestyles='-', lw=1,
label='frozen pmf')
ax.legend(loc='best', frameon=False)
plt.show()
连续分布
均匀分布
若a,b为有限数,由下列密度函数定义的分布
称为[a, b].上均匀分布:
或
plt.plot(np.linspace(-4,4,100),stats.uniform.pdf(np.linspace(-4,4,100)))
plt.fill_between(np.linspace(-4,4,100),stats.uniform.pdf(np.linspace(-4,4,100)),alpha=0.15)
plt.plot(np.linspace(-4,4,100),stats.uniform.cdf(np.linspace(-4,4,100)))
plt.text(x=-1.5,y=0.7,s="pdf(uniform)",rotation=65,alpha=0.75,weight="bold",color="b")
plt.text(x=-0.4,y=0.5,s="cdf",rotation=55,alpha=0.75,weight="bold",color="r")
Text(-0.4, 0.5, 'cdf')

正态分布
一个正态分布用X~N(μ,1/τ)表示,它带有两个参数:均值μ和精准度τ。这里用1/τ代替了σ2,主要是因为这样能简化数据分析。记住:τ越小,分布越宽(即我们越不能确定);τ越大,分布越窄(即我们越能确定)。不管怎么样,τ永远为正数。
一个服从N(μ,1/τ)的随机变量的概率密度函数如下:
# 展示正态分布的不同密度函数
figsize(12.5, 4)
nor = stats.norm
x = np.linspace(-8, 7, 150)
mu = (-2, 0, 3)
tau = (.7, 1, 2.8)
parameters = zip(mu, tau)
for _mu, _tau in parameters:
plt.plot(x, nor.pdf(x, _mu, scale=1./_tau),
label="$\mu = {},\;\\tau = {:.1f}$".format(_mu, _tau))
plt.fill_between(x, nor.pdf(x, _mu, scale=1./_tau),alpha=.33)
plt.legend(loc="upper right")
<matplotlib.legend.Legend at 0x277b3db7748>

指数分布
指数可以取任意非负值,包括非整数
对指定的参数λ,指数型随机变量的期望值为λ的逆
a = np.linspace(0, 4, 100)
expo = stats.expon
lambda_ = [0.2,0.5, 1]
for l in lambda_:
plt.plot(a, expo.pdf(a, scale=1./l), lw=3, label="$\lambda = {:.1f}$".format(l))
plt.fill_between(a, expo.pdf(a, scale=1./l),alpha=.33)
plt.legend()
plt.ylabel("PDF at $z$")
plt.xlabel("$z$")
plt.ylim(0,1.2)
(0.0, 1.2)

gamma = stats.gamma
fig, ax = plt.subplots(1, 1)
a = 1.99
mean, var, skew, kurt = gamma.stats(a, moments='mvsk')
x = np.linspace(gamma.ppf(0.01, a),
gamma.ppf(0.99, a), 100)
ax.plot(x, gamma.pdf(x, a),
'r-', lw=5, alpha=0.6, label='gamma pdf')
rv = gamma(a)
ax.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')
r = gamma.rvs(a, size=1000)
ax.hist(r, density=True, histtype='stepfilled', alpha=0.2)
ax.legend(loc='best', frameon=False)
plt.show()

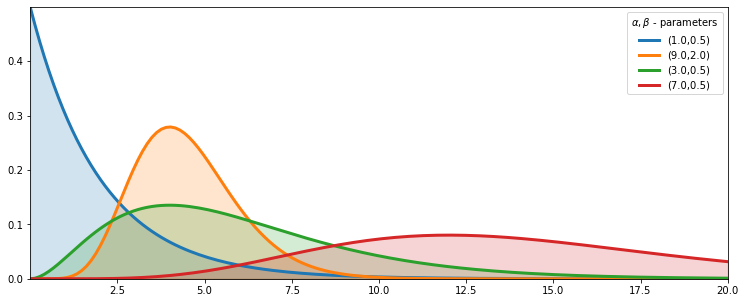
Gamma分布
指数分布解决的问题是“要等到一个随机事件发生,需要经历多久时间”,伽玛分布解决的问题是“要等到n个随机事件都发生,需要经历多久时间”。所以,伽玛分布可以看作是n个指数分布的独立随机变量的加总。
figsize(12.5, 5)
parameters = [(1, 0.5), (9, 2), (3, 0.5), (7, 0.5)]
x = np.linspace(0.001 ,20, 150)
for alpha, beta in parameters:
y = gamma.pdf(x, alpha, scale=1./beta)
lines = plt.plot(x, y, label = "({:.1f},{:.1f})".format(alpha,beta), lw = 3)
plt.fill_between(x, 0, y, alpha = 0.2, color = lines[0].get_color())
plt.autoscale(tight=True)
plt.legend(title=r"$\alpha, \beta$ - parameters")
<matplotlib.legend.Legend at 0x277b3c247b8>
Beta分布
Beta分布的密度函数为:
figsize(12.5, 4)
datas = np.linspace(0, 1, 200)
plt.fill_between(datas,stats.beta.pdf(datas, a=5, b=10),hatch="+")
plt.fill_between(datas,stats.beta.pdf(datas, a=100, b=20),hatch="//")
plt.fill_between(datas,stats.beta.pdf(datas, a=20, b=60),hatch="*")
<matplotlib.collections.PolyCollection at 0x277b4184710>















)



 因为好奇)
