在SPSS统计分析交流群中有学员在阅读论文的过程中看到下面的这张表格：

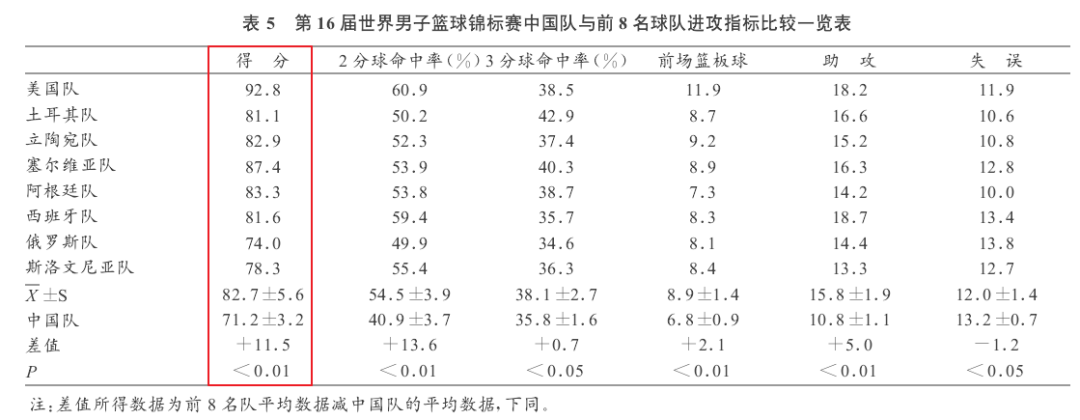
这张表中记录了第16届世界男子篮球锦标赛中国队与前8名球队进攻指标比较的结果，其中这份表格并没有给出详细的P值，而只是告诉我们P值小于多少。

在这种只有汇总数据，没有明细数据的情况下，这位学员希望根据这张表中呈现的数据信息计算出详细的P值。

解答这个问题需要用到“摘要独立样本t检验”知识点，只要我们分别知道了两组数据的样本量、均值和标准差，就能通过SPSS进行t检验分析，得到两组数据比较的t值和显著性P值。

但在这张表格中，我们只能够获得数据的均值和标准差，而不知道数据的样本量，因此无从开展数据分析。

我通过关键词搜索的方式，在中国知网上找到了学员阅读的这篇论文《第16届世界男子篮球锦标赛各球队攻防能力的比较研究》，仔细阅读了这篇论文，发现了如下的补充信息：

我大概判断出在第16届世界篮球锦标赛中，中国队应该是打了5场篮球赛进入16强，场均得分是71.2，标准差是3.2；世锦赛前8名的队伍的平均得分是82.7，标准差是5.6。因此，我们可以根据获得的这些汇总信息计算出中国队与前8名球队在整体得分上的显著性差异值。

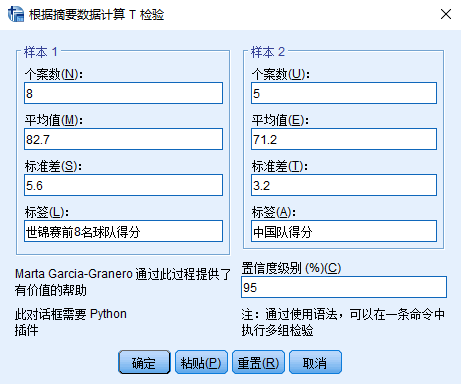
操作步骤：选择菜单分析 -> 比较平均值 -> 摘要独立样本t检验，将两组数据的数值分别填入对应的样本信息框中，点击确定。

注：该功能需要使用SPSS25.0或26.0版本才能实现，且需要在安装SPSS时同步安装Python扩展插件，文末推荐的课程中提供了该版本的软件。

摘要独立样本t检验的对话框如下图所示：

得到的分析结果如下所示：

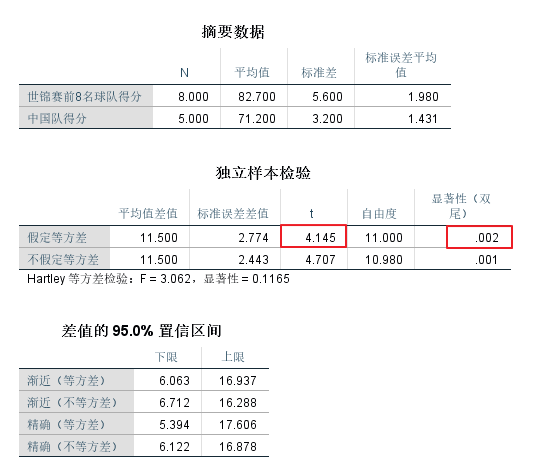
从上图的分析结果可知：中国男子篮球队的综合平均得分与第16届世锦赛前8名的队伍的平均得分进行独立样本t检验，得到的t值为4.145，显著性P值为0.002(P＜0.01)，说明在99%的置信区间内，两者之间的差异有统计学意义。

表中其它进攻指标(2分球命中率、3分球命中率、进攻篮板球数、助攻、失误)因为原论文中缺少样本量信息(或者我因为缺乏体育比赛的知识而没有找出其得分次数信息)，所以我们不能对它们的比较结果进行复盘。

这个小案例也提醒大家，在进行论文写作的过程中，应该详细汇报数据的基本信息，至少应该包括样本量、均值、标准差、P值等统计量，以便让自己的论文更有说服力和可重复性。

以上就是我针对这位学员的提问所进行了回复，也向大家分享了摘要独立样本t检验方法，这种方法主要用于这种没有明细数据，只有汇总数据的情况，在研读他人的论文数据分析结果的过程中经常会使用到。

更多有关t检验的介绍可见松鼠的课程《SPSS论文数据分析实战》，点击文末阅读原文即可了解课程详情哦~

参考论文：

胡茂全, 孙庆祝, 荣华. 第 16 届世界男子篮球锦标赛各球队攻防能力的比较研究[D]. , 2011.