推荐系统——GBDT+LR

[[逻辑回归模型]]

逻辑回归是在[[线性回归]]的基础上添加了一个Sigmoid函数（非线形）映射，从而可以使逻辑回归成为一个优秀的分类算法
逻辑回归假设数据服从[[伯努利分布]]，通过[[极大化似然函数]]的方法，运用[[梯度下降]]来求解参数，来达到将数据二分类的目的。
相比于[[协同过滤]]和[[矩阵分解]]利用用户的物品“相似度”进行推荐，LR将问题看成一个分类问题，通过预测正样本的概率对物品进行排序，因此逻辑回归模型将推荐问题转化成了一个点击率预估问题。

逻辑回归做推荐的步骤

将用户年龄、性别、物品属性、物品描述、当前时间、当前地点等特征转成数值向量
确定逻辑回归的优化目标，比如把点击率预测转换成二分类问题，这样就可以得到分类问题常用的损失作为目标，训练模型
在预测的时候，将特征向量输入模型产生预测，得到用户“点击”物品的概率
利用点击概率对候选物品排序，得到推荐列表

![[Pasted image 20201030171926.png]]

对于LR模型而言，主要关键为求出每个特征的权重参数 $w$ ，一般是使用梯度下降的方式

优点：

LR模型形式简单，可解释性好，从特征的权重可以看到不同的特征可以看到不同的特征对最后结果的影响
训练时便于并行化，在预测时只需要对特征进行线性加权，所以性能比较好，适合处理海量id类特征，且使用id类特征有一个很重要的好处，即防止信息损失（相对于范化的CTR特征），对于头部资源会有更细致的描述
资源占用少尤其内存，在实际的工程应用中只需要存储权重比较大的特征及特征对应的权重
方便对输出结果调整。LR可以方便的得到最后的分类结果，因为输出的是每个样本的概率分数，我们可以很容易的对这个概率分数进行阈值的划分。

缺点：

无法进行特征交叉得到更多信息
准确率并不是很高
处理非线性数据比较麻烦，LR在不引入其他方法的情况下，只能处理线性可分的数据，如果想处理非线性，首先需要对连续特征的处理进行离散化
LR需要进行人工特征组合

所以如何自动发现有效的特征、特征组合，弥补人工经验不足，缩短LR特征实验周期，可以交由[[GBDT]]来做，它可以自动发现特征并进行有效组合

[[GBDT]]模型

GBDT名为梯度提升树，是传统机器学习中对真实分布拟合最好的几种算法之一
GBDT通过采用加法模型（即基函数的线性组合），以及不断减小训练过程产生的误差来达到将数据分类或者回归的算法。
GBDT每轮产生一个弱分类器，每个分类器在上一轮分类器的残差基础上进行训练。GBDT对弱分类器的要求只要求足够简单，并且地方低方差高偏差（欠拟合）。由此，每个分类回归树的深度不会很深，最终的总分类器是将每轮训练得到的弱分类器加权求和得到。
GBDT来解决二分类和回归问题的本质一样，都是通过不断构建[[决策树]]，使预测结果一步步接近目标值。
GBDT在回归问题上一般使用平方损失，而在二分类问题中，GBDT和逻辑回归一样，使用交叉熵

构建分类GBDT的过程：

初始化GBDT
分类GBDT的初始状态只有一个叶子节点，该节点为所有样本的初始预测值： $F0(x)=argmin⁡γ∑i=1nL(y,γ)F_0(x) = arg \min_{\gamma} \sum_{i=1}^n L(y, \gamma)$
其中， $F$ 代表GBDT模型， $F_0$ 是模型的初识状态，该式子的意思是找一个 $γ\gamma$ ，使所有的样本的 $L o s s$ 最小，而 $γ\gamma$ 表示节点的输出，即叶子节点，是一个 $log(ηi)log(\eta_i)$ 形式的回归值，在初始状态, $γ=F0\gamma = F_0$

具体例子可以参考学习资料中例子P59

GBDT的优缺点：
对于GBDT而言，生成树的过程实际上就是自动进行多维度的特征组合的过程，从根节点到叶子节点上的整个路径（多个特征值判断），才能最终决定一棵树的预测值，另外，对于连续型特征的处理，GBDT可以拆分出一个临界阈值。
而GBDT对于海量的id类特征，GBDT由于树的深度和树的数量限制（防止过拟合），不能有效存储；另外海量特征也会存在性能瓶颈，当GBDT的one hot特征大于100k维时，需要做分布式训练才能保证不爆内存，因此，GBDT通常配合少量的反馈CTR特征来表达，在带来一定范化能力的同时会有信息损失，对于头部资源无法有效表达。
因此提出GBDT+LR

GBDT+LR

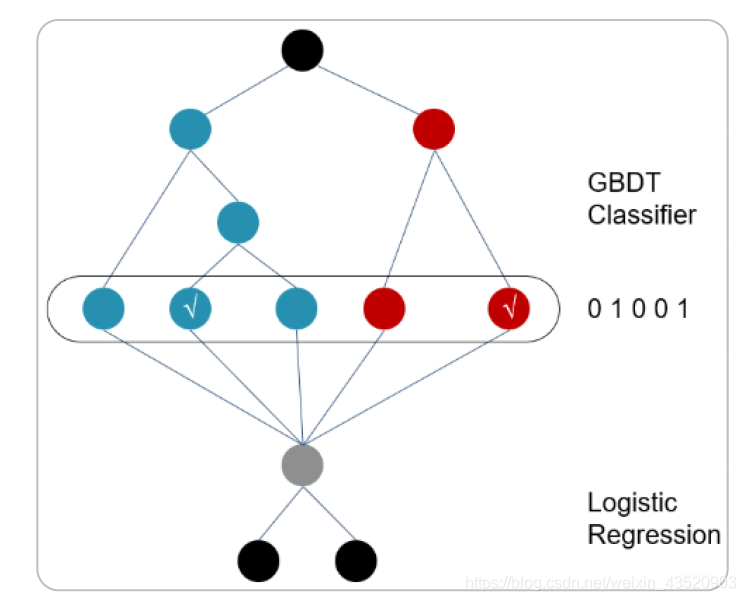
GBDT+LR：先利用GBDT进行特征筛选和组合进而生成新的离散特征向量，再把该特征向量当作LR模型的输入，来产生的最后的预测结果。