棋盘切割 DP POJ 1191

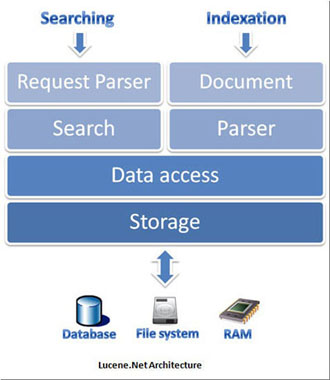
把方差公式先变形为 σ² = (1/n)∑xi²-x_a²

x_a为平均值。

由于要求标准差最小，只需方差最小，平均值都是一样的，n也是一样的，这样原问题就变为求这n快小棋盘总分的平方和最小

考虑左上角为（x1,y1）,右上角为（x2,y2）的棋盘，设该棋盘切割K次后得到的K+1块矩形的总分平方和最小值为d[k,x1,y1,x2,y2]。该棋盘的总分平方和为

s[x1,y1,x2,y2].则它可以沿着横线切，也可以沿着竖线切，然后选一块继续切（这里可以用递归完成）

状态转移方程为d[k,x1,y1,x2,y2] =  min{

min{ d[k-1,x1,y1,a,y2] + s[a+1,y1,x2,y2] , d[k-1,a+1,y1,x2,y2] + s[x1,y1,a,y2] },    (x1 <= a < x2)

min{ d[k-1,x1,y1,x2,b] + s[x1,b+1,x2,y2] , d[k-1,x1,b+1,x2,y2] + s[x1,y1,x2,b] }  （y1 <= b < y2）

}

贴代码：

#include <cstdio>
#include <cstring>
#include <cmath>
#define N 9
#define min(a,b) a<b?a:b
#define INF 100000000
int n;
int map[N][N];
int presum[N][N];
int d[16][N][N][N][N];//用d[k][x1][y1][x2][y2]表示左上角为（x1,y1）
//右下角为(x2,y2)的棋盘切成了k+1块时最小的总分平方和值
void presolve()
{
    //预处理，算出所有左上角为（1，1）的所有矩阵元素和
    int i,j;
    for(i=0; i<=N; ++i)
        presum[0][i] = 0,presum[i][0] = 0;
    for(i=1; i<N; ++i)
    {
        int rowsum = 0;
        for(j=1; j<N; ++j)
        {
            scanf("%d",&map[i][j]);
            rowsum += map[i][j];
            presum[i][j] = presum[i-1][j] + rowsum;
        }
    }
}
int rectSquare(int x1,int y1,int x2,int y2)
{
    //计算左上角为(x1,y1),右下角为(x2,y2)的棋盘的总分平方和
    int ret = presum[x2][y2] -presum[x1-1][y2] -presum[x2][y1-1] +presum[x1-1][y1-1];
    return ret*ret;
}
//DP程序
int DP(int k,int x1,int y1,int x2,int y2)
{
    int t,c,e;
    int MIN = INF;//用来求最后的d[k][x1][y1][x2][y2]
    if(d[k][x1][y1][x2][y2] != -1)//记忆化搜索？？？已经求过了，不再求，直接用
        return d[k][x1][y1][x2][y2];
    if(k == 0)//切0刀，不就是该棋盘了吗？最小值也是该棋盘的总分平方和，边界条件
        return d[k][x1][y1][x2][y2]=rectSquare(x1,y1,x2,y2);
    for(int a = x1; a < x2; ++a)
    {
        //横着切成了两块
        c = rectSquare(a+1,y1,x2,y2);
        e = rectSquare(x1,y1,a,y2);
        t = min(DP(k-1,x1,y1,a,y2) + c,DP(k-1,a+1,y1,x2,y2) + e);//选取一块继续切割
        MIN = min(MIN,t);
    }
    for(int b = y1; b < y2; ++b)
    {
        //竖着切成了两块
        c = rectSquare(x1,b+1,x2,y2);
        e = rectSquare(x1,y1,x2,b);
        t= min(DP(k-1,x1,y1,x2,b)+c,DP(k-1,x1,b+1,x2,y2)+e);//选取一块继续切割
        MIN = min(MIN,t);
    }
    d[k][x1][y1][x2][y2] = MIN;//所有的情况都考虑完后，所得就是该最小值
//    printf("d[%d][%d][%d][%d][%d] = %d\n",k,x1,y1,x2,y2,d[k][x1][y1][x2][y2]);
    return MIN;
}
int main()
{
//    freopen("in.cpp","r",stdin);
    scanf("%d",&n);
    presolve();
    memset(d,-1,sizeof(d));
    int sumsquare = DP(n-1,1,1,8,8);
    double f = n*sumsquare - presum[8][8]*presum[8][8];
    f = sqrt(f)/n;
    printf("%.3f\n",f);
//    printf("%d\n",0x7fffffff);
    return 0;
}

注意：
用double，然后用%.3lf WA
用%.3fAC
在DP时min的初始值赋为10^7WA
赋为10^8AC
这点我还比较想得通，棋盘最大的总分和为6400，最大的平方和即为6400^6400,为40960000
你赋的min值至少应该大于这个数，否则就不对了，所以10^7可能会错
我中间赋过一个0x7fffffff，竟然导致出现了负数，怎么会啊。。。。。不了解
补充:我现在理解了为什么出现负数，因为0x7fffffff是最大的整数数了，再加就溢出了，成为负的了·····