在上一期,我们介绍了一种特殊的数据结构 “哈夫曼树”,也被称为最优二叉树。没看过的小伙伴可以点击下方链接:
漫画:什么是 “哈夫曼树” ?
那么,这种数据结构究竟有什么用呢?我们今天就来揭晓答案。




计算机系统是如何存储信息的呢?
计算机不是人,它不认识中文和英文,更不认识图片和视频,它唯一“认识”的就是0(低电平)和1(高电平)。
因此,我们在计算机上看到的一切文字、图像、音频、视频,底层都是用二进制来存储和传输的。
从狭义上来讲,把人类能看懂的各种信息,转换成计算机能够识别的二进制形式,被称为编码。
编码的方式可以有很多种,我们大家最熟悉的编码方式就属ASCII码了。
在ASCII码当中,把每一个字符表示成特定的8位二进制数,比如:
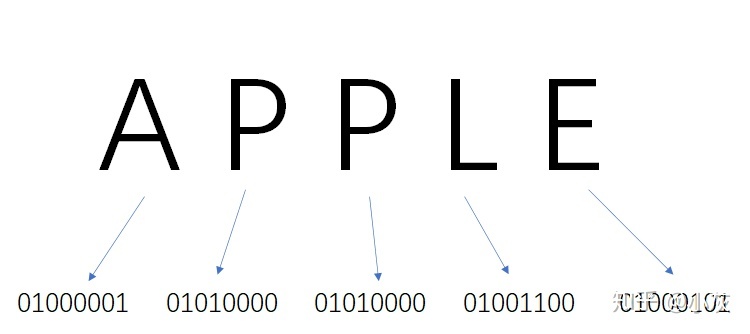
显然,ASCII码是一种等长编码,也就是任何字符的编码长度都相等。




为什么这么说呢?让我们来看一个例子:
假如一段信息当中,只有A,B,C,D,E,F这6个字符,如果使用等长编码,我们可以把每一个字符都设计成长度为3的二进制编码:
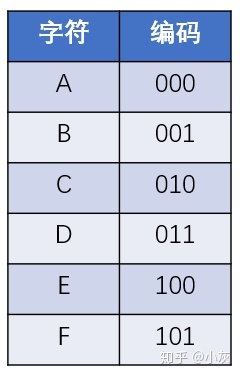
如此一来,给定一段信息 “ABEFCDAED”,就可以编码成二进制的 “000 001 100 101 010 011 000 100 011”,编码总长度是27。

但是,这样的编码方式是最优的设计吗?如果我们让不同的字符对应不同长度的编码,结果会怎样呢?比如:
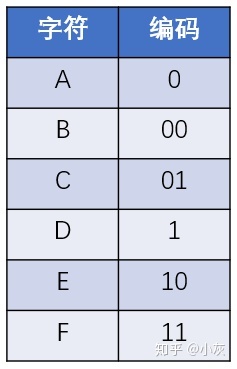
如此一来,给定的信息 “ABEFCDAED”,就可以编码成二进制的 “0 00 10 11 01 1 0 10 1”,编码的总长度只有14。
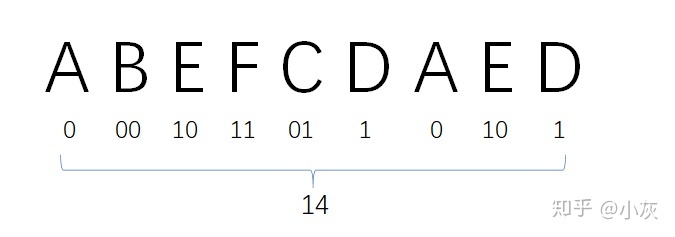



哈夫曼编码(Huffman Coding),同样是由麻省理工学院的哈夫曼博所发明,这种编码方式实现了两个重要目标:
1.任何一个字符编码,都不是其他字符编码的前缀。
2.信息编码的总长度最小。



哈夫曼编码的生成过程是什么样子呢?让我们看看下面的例子:
假如一段信息里只有A,B,C,D,E,F这6个字符,他们出现的次数依次是2次,3次,7次,9次,18次,25次,如何设计对应的编码呢?
我们不妨把这6个字符当做6个叶子结点,把字符出现次数当做结点的权重,以此来生成一颗哈夫曼树:
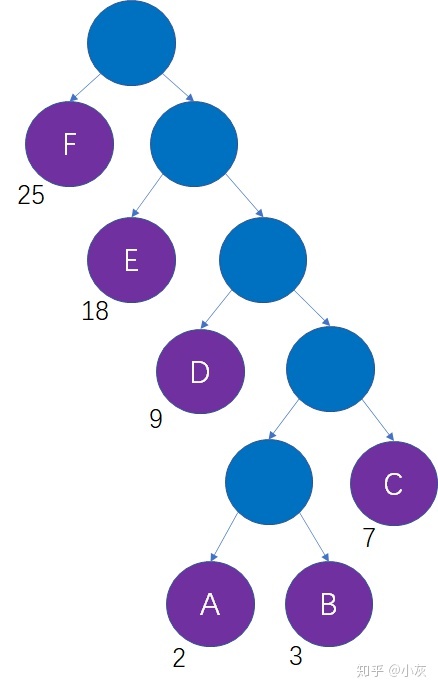
这样做的意义是什么呢?
哈夫曼树的每一个结点包括左、右两个分支,二进制的每一位有0、1两种状态,我们可以把这两者对应起来,结点的左分支当做0,结点的右分支当做1,会产生什么样的结果?
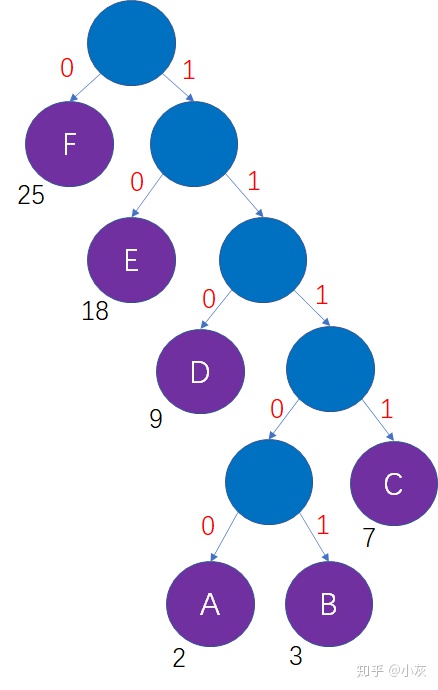
这样一来,从哈夫曼树的根结点到每一个叶子结点的路径,都可以等价为一段二进制编码:
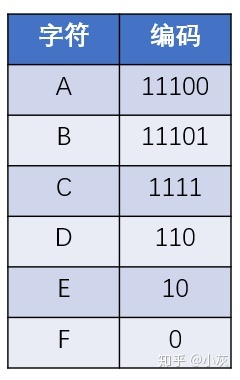
上述过程借助哈夫曼树所生成的二进制编码,就是哈夫曼编码。
现在,我们面临两个关键的问题:
首先,这样生成的编码有没有前缀问题带来的歧义呢?答案是没有歧义。
因为每一个字符对应的都是哈夫曼树的叶子结点,从根结点到这些叶子结点的路径并没有包含关系,最终得到的二进制编码自然也不会是彼此的前缀。
其次,这样生成的编码能保证总长度最小吗?答案是可以保证。
哈夫曼树的重要特性,就是所有叶子结点的(权重 X 路径长度)之和最小。
放在信息编码的场景下,叶子结点的权重对应字符出现的频次,结点的路径长度对应字符的编码长度。
所有字符的(频次 X 编码长度)之和最小,自然就说明总的编码长度最小。








privateNode root;privateNode[] nodes;//构建哈夫曼树publicvoid createHuffmanTree(int[] weights){//优先队列,用于辅助构建哈夫曼树Queue<Node> nodeQueue =newPriorityQueue<>();nodes =newNode[weights.length];//构建森林,初始化nodes数组for(int i=0; i<weights.length; i++){nodes[i]=newNode(weights[i]);nodeQueue.add(nodes[i]);}//主循环,当结点队列只剩一个结点时结束while(nodeQueue.size()>1){//从结点队列选择权值最小的两个结点Node left = nodeQueue.poll();Node right = nodeQueue.poll();//创建新结点作为两结点的父节点Node parent =newNode(left.weight + right.weight, left, right);nodeQueue.add(parent);}root = nodeQueue.poll();}//输入字符下表,输出对应的哈夫曼编码publicString convertHuffmanCode(int index){return nodes[index].code;}//用递归的方式,填充各个结点的二进制编码publicvoid encode(Node node,String code){if(node ==null){return;}node.code = code;encode(node.lChild, node.code+"0");encode(node.rChild, node.code+"1");}publicstaticclassNodeimplementsComparable<Node>{int weight;//结点对应的二进制编码String code;Node lChild;Node rChild;publicNode(int weight){this.weight = weight;}publicNode(int weight,Node lChild,Node rChild){this.weight = weight;this.lChild = lChild;this.rChild = rChild;}@Overridepublicint compareTo(Node o){returnnewInteger(this.weight).compareTo(newInteger(o.weight));}}publicstaticvoid main(String[] args){char[] chars ={'A','B','C','D','E','F'};int[] weights ={2,3,7,9,18,25};HuffmanCode huffmanCode =newHuffmanCode();huffmanCode.createHuffmanTree(weights);huffmanCode.encode(huffmanCode.root,"");for(int i=0; i<chars.length; i++){System.out.println(chars[i]+":"+ huffmanCode.convertHuffmanCode(i));}}
这段代码中,Node类增加了一个新字段code,用于记录结点所对应的二进制编码。
当哈夫曼树构建之后,就可以通过递归的方式,从根结点向下,填充每一个结点的code值。


在公众号后台回复“学习视频”,可以获得海量免费的IT视频课程哦~~


:Vue的终极解决方案)

方法的返回值说明)

:webpack横幅plugin的使用)

的一些理解)

:htmlwebpackplugin的使用)



:uglifyjswebpackplugin的使用)
和调用(CALL)及变量创建(DECLARE)和赋值(SET)操作方法...)
![bzoj2060[USACO2010,Nov]Visiting Cows拜访奶牛](http://pic.xiahunao.cn/bzoj2060[USACO2010,Nov]Visiting Cows拜访奶牛)
:webpack-dev-server搭建本地服务)

