前文我们介绍了基于Arnold置乱的数字图像加密算法的两种图像置乱变换,今天我们介绍的是另外三种图像置乱变换:基于骑士巡游的图像置乱变换、基于Arnold变换的数字图像置乱和基于仿射变换的置乱变换。
一、基于骑士巡游的图像置乱变换
所谓骑士巡游,就如同象棋一样,给出一块具有n²个格子的n×n棋盘,一位骑士(knight)按国际象棋规则移动,放在初始坐标为(x0,y0)的格子里,骑士巡游问题(Knight-tour Problem)就是要求寻找一种方案使之过每个格子一次,且仅一次。该问题可以较自然地推广到n×m棋盘。一个9×9棋盘的骑士巡游路线如下面的矩阵T所示,称其为巡游矩阵,其中1表示骑士巡游的起点,t(i, j)的值表示其实第t(i, j)步巡游到i行j列。
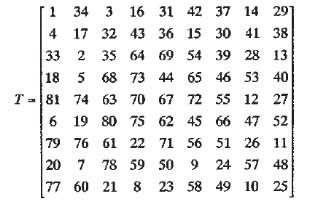
骑士巡游变换:对于图像A={a(i, j)}nxm,用巡游矩阵T={t(i, j)}nxm作置乱变换,得到图像B。其变换方法如下:将A与T按行列作一一对应,将A中与T中位置1对应(下简称对应位置)的像素灰度值(或R、G、B分量值)移到对应位置2,将对应位置2的像素灰度值移到对应位置3,......以此类推,最后将对应nxm位置的像素灰度值移动对应位置1,就得到了按T置乱后的图像B。这种按骑士巡游路径进行置乱的变换,简称为骑士巡游变换。
按骑士巡游变换对图像作置乱,不仅可以隐藏图像细节,而且可以使用图像总的形象保持不变,用骑士巡游变换来作图像的隐藏,其保密度是比较高的。密钥个数大于Hilber曲线、Peano方法、E-曲线、幻方置乱变换的密钥个数。通过骑士巡游起点和终点的选取、巡游方向的变化以及挖洞的位置和数量的确定来构成不同的密钥,它既适合单密钥体制,所以其保密度较高。
骑士巡游交换具有以下优点:
(1)适用于高和宽不同的图像,而幻方变化仅适用于高和宽相同的图像;
(2)置乱方法灵活,可通过编程来控制巡游的起点、终点以及巡游的方向,还可控制一些点不巡游(挖洞),从而得到不同的置乱方法;
(3)不仅能隐藏图像的细节,而且特别能隐藏图像中的文字信息,也可应用于其他计算机文件的加密。骑士巡游变换同样具有周期性,其变换周期就是n²。
二、基于Arnold变换的数字图像置乱

这是对一个一般的二维可逆保面积映射加了取正整数的限制,这种变换具有拉伸和折叠的性质,经变换后原来相邻的亮点(i, j)和(i, j+1)经几次迭代后就不再相邻,这样图像经迭代若干次后就变得不可辨认,从而达到加密的效果。当|A|=+1时,变换后的图像保持面积不变。由于这是一种双射而且图像是一个有限点集,所以反复变换必然能够恢复到原来的位置,即变换具有周期性,从而对加密图像只需继续变换相应的次数就能对图像解密。若P满足一定条件,此变换具有周期性,其周期与图像大小和内容没有直接联系。Arnold变换实际上是一种点的位置移动,且这种变换是一一对应的。Arnold变换仅有4个参数,用户数据加密尚嫌太少。

所以变换的周期T是使下式成立的最小自然数m:Am(mod N)=E,其中E为单位矩阵。这样就很容易通过编程求出变换的周期。
A作为加密矩阵应具有以下特点:映射是单的,满的。即:保持图像面积的不变性。
加密因子a,b,c,d都是整数,因为图像中作为离散的点都是取整数的。
变换具有周期性或可逆,以保证加密后可以解密。
三、基于仿射变换的置乱变换
仿射变换是几何中感到一种常见变换,它可以分解成:运动变换、斜对称变换、相似变换、压缩(拉伸)变换、正交变换、剪移等变换的组合,其矩阵形式:
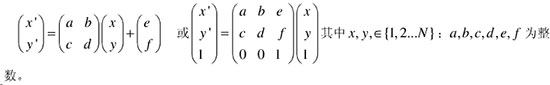
从数据加密角度考虑,仿射变换的参数有6个,比Arnold变换增加了两个,从密钥角度出发,增加了大量的密钥。
虽然对于平面仿射变换由三对对应点代入后就可完全确定,但由于目的是要它作图像的置乱。因此对仿射变换还有特殊的要求,即:要寻找恰当的系统数使得变换是区域{1,2...N}到自身的单映射和满映射。我们可以从仿射变换的特点出发,从而可求得满足要求的一系列解。求得的系数可作为图像置乱加密的密钥。
定义1:上式是仿射变换的必要条件是:ad-bc=+1.
证明:根据仿射变换的定义,变换前后的图像面积保持不变,即图像所在区域的几何面积不变,因此ad-bc=+1。
作为数字图像加密的仿射变换是不容易求出的,需要很强的技巧。下面是三种交换:
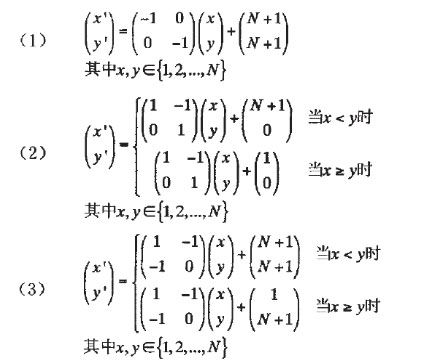
和Arnold变换相类似,这是一种二维可逆保面积映射加了一定的限制条件,这种变换具有拉伸和折叠的性质,经变换后原来相邻的两点(i, j)和(i, j+1)经几次迭代后就不再相邻,这样副图像经迭代若干次后就变得不可辨认,从而达到加密的效果。由于这是一种双射而且图像是一个有限点集,所以反复变换必然能够恢复到原来的位置,即变换具有周期性,从而对加密图像只需继续变换相应的次数就能对图像解密。根据仿射变换的定义,容易得到下面的性质:
性质1:仿射变换的积仍是仿射变换。
性质2:仿射变换的和不是仿射变换。
性质3:仿射变换的逆一定存在,且仍是仿射变换。
仿射变换用于图像置乱有较好的效果。在经过一定的迭代置乱变换后,可将图像的各种灰度值均匀的分布到图像区域中,从而能较好的隐藏原图像的信息。另外由于这种仿射变换是双射且图像是由有限个点组成的,所以经过一定的迭代次数后能够得到原图像。

也可以利用仿射变换的逆变换对图像进行加密,这就增加了一种新的加密算法,而且它和仿射变换具有相似的性质。
仿射变换避免了取模运算,从而运算速度快,它的逆交换也具有简洁的解析表达式,使得解密过程无需进行周期次数的迭代。该新变换只需进行十几次的迭代过程就可以使图像完全置乱,因此它即可作为图像加密的变换方法,另一方面,从信息隐藏的角度考虑,图像置乱变换作为信息隐藏的预处理,如置乱后再进行隐藏,Arnold变换在进行迭代置乱时,有较强的纹理特征,而仿射变换使得图像置乱后,其中灰度值均匀的分布在图像所在的区域,减少了置乱图像的纹理特征,从而提供了信息的安全性。
 扩展python)




:vue指令v-for key)
)


:小游戏设计)


:vue指令v-if)



:动态绑定样式)
)

