第5章学习树和二叉树
树
1.树的结构定义是一个递归定义:树的定义中又用到树的定义
2.结点的度即为结点的分支数,树的度是树内各结点度的最大值,二叉树每个结点至多只有两颗子树(即二叉树中不存在度大于2的结点)
二叉树
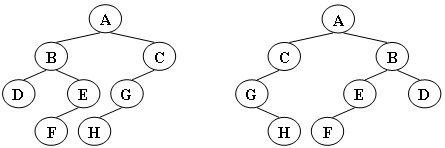
1.二叉树的子树有左右之分,次序不能颠倒
2. Ⅰ 深度为k的二叉树至多有2^k-1个结点(每层2^(i-1)个,用等比数列求和公式得出结果)
Ⅱ n0=n2+1 证明
其中—— 终端结点数:n0 度为1的结点数:n1 度为2的结点数:n2 结点总数:n 分支总数:B
n = n0 + n1 + n2 ①
n = B + 1 ② //每个结点都对应有一个分支在脑袋上 以及一个根结点
B = n1 + 2 n2 ③ //分支由度为1或2的结点射出
由②③得 n = n1 + 2 n2 + 1 ④
由①④证得 n0=n2+1
Ⅲ 具有n个结点的完全二叉树的深度为 k=⌊log2(n)⌋ + 1
3.顺序存储二叉树,数组的下标可以从1开始。当为完全二叉树时,父子结点的下标关系为 左孩子 = 父*2 右孩子 = 父*2 + 1;缺点:不利于增删 只适用于完全二叉树,否则空间浪费
4.链式存储二叉树
![[html] 浏览器内多个标签页之间的通信方式有哪些?](http://pic.xiahunao.cn/[html] 浏览器内多个标签页之间的通信方式有哪些?)

 MySQL体系结构概述)
![[html] 元素的alt和title有什么区别?](http://pic.xiahunao.cn/[html] 元素的alt和title有什么区别?)



![[html] 你认为table的作用和优缺点是什么呢?](http://pic.xiahunao.cn/[html] 你认为table的作用和优缺点是什么呢?)



![[html]请描述HTML元素的显示优先级](http://pic.xiahunao.cn/[html]请描述HTML元素的显示优先级)



---Java语言)
![[html] 关于<form>标签的enctype属性你有哪些了解?](http://pic.xiahunao.cn/[html] 关于<form>标签的enctype属性你有哪些了解?)

![[html] 说说你对属性data-的理解](http://pic.xiahunao.cn/[html] 说说你对属性data-的理解)
