planning algorithms chapter 2

planning algorithms chapter 2 :Discrete Planning

离散可行规划导论

问题定义

离散可行规划

在离散规划中，状态是“可数”的，有限的。
离散可行规划:

非空状态空间 X
对于每个状态 x，存在一个有限的动作空间 U(x)
对于每个状态和动作空间，存在状态转移方程，产生一个新的状态
一个初始状态 xi
一个目标集 Xg

为了方便表达离散可行规划的定义，通常采用有向状态转移图来表示，图上的顶点集合表示状态空间 X，只有当两顶点之间可状态转移时，图上两顶点之间的有向边才存在。初始状态和目标集可以表示为图上特别指定的顶点。

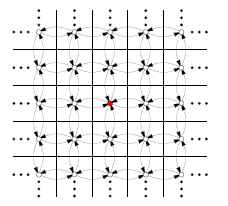
有向状态转移图

离散规划的例子

2D 网格上移动（“迷宫”）

魔方拼图

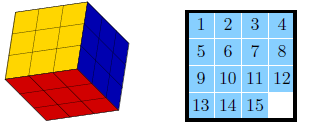
图搜索算法

前向搜索算法

通用前向图搜索算法模板

上图显示了通用图搜索算法模板，其中有几点需要注意：Q 内部如何排序，如何判断状态属于目标状态，如何得到计划（动作序列)，如何判断该状态是否已经访问过，是否需要更新状态代价值（如在Dijkstra 和 A* 算法）

几种前向搜索算法，区别在于定义了Q 这个优先级队列内部不同的排序方式

广度优先：FIFO
深度优先：LIFO
Dijkstra ：一种图单源最短路径搜索算法，一种特殊的动态规划形式
在Dijkstra中，图上每条边附带一个代价（l(x, u) >= 0），Q 内部是按照从初始状态到达该状态的累计代价（C(x),cost-to-come）排序。cost-to-come 在搜索过程中通过DP方式来增量计算（C(x‘) = C(x) + l(x, u), 代表最优)。
Dijkstra 可以保证一旦某个状态被访问，则该状态的 cost-to-come一定是最优的。Dijkstra 内部 Q 实现采用的 Fibonacci heap 这种数据结构，可以实现在常数时间内判断某个状态是否被访问过。
A-star ：基于Dijkstra进行扩展，引入启发项值（G(x)，cost-to-go)，当G(x) = 0 时， A-star 退化成Dijkstra，Q 内部是按照从初始状态到达目标状态的预估最优代价( C(x’) + G(x‘)) 进行排序。
最佳优先搜索：Q 内部是按照 cost-to-go 排序，一种贪心搜索，不保证最优，但搜索速度快。
迭代加深搜索：通过不断增加深度优先搜索深度的一种搜索，将深度优先搜索转换为一种系统性搜索方式（能够访问可到达的所有状态)。
迭代加深搜索相比 BFS 使用更少的内存，迭代加深搜索结合 A-star 的思想，形成了 IDA* 算法，在每次迭代过程中，最大深度步长为C(x’) + G(x‘)。

其他搜索算法

反向搜索算法

通用反向搜索算法模板

双向搜索算法

通用双向搜索算法模板
当两棵搜索树相遇时，搜索结束，返回成功。如果其中任一搜索树的优先级队列为空，且两颗树未相遇，则搜索结束，返回失败。

搜索算法的统一视角

上述所有的搜索算法遵循以下一些共同的模式：

初始
搜索开始时，搜索图 G(V,E)中 E为空集，V只包含初始状态
选择顶点
从V中选择一个顶点，这通常是通过维护一个优先级队列实现
应用动作
基于V中选择的某个顶点，应用动作后，生成一个新的状态 x = f(x0, u)
向搜索图中插入有向边
新状态 x 如果不在 V 中，则将 x 插入到 V 中
检查解决方案
如果只有一颗搜索树，根据搜索图 G 得到从初始状态到目标状态的路径会比较简单。如果搜索树数量大于 1 颗，复杂度会增加。
返回到步骤 2
迭代直到找到一个解决方案。

离散最优规划

最优定长规划

离散定长最优规划
$L\left ( \pi _{K} \right ) = \sum_{k=1}^{K}l(x_{k},u_{k}) + l_{F}(x_{F})$

通过引入代价项Lf(xf)这一技巧，将离散可行规划中的约束转换为优化问题代价函数中的一项。

基本思想: 最优规划解决方案的子组成方案也是最优的，于是可以通过动态规划方法解决。在最优定长规划中，采用一种迭代算法，称为值迭代，它的主要思想是在状态空间中迭代计算最优的 cost-to-go(或 cost-to-come)。Dijkstra’s algorithm 也是值迭代的一种方式。

反向值迭代

基本思想：在状态空间中迭代计算最优的 cost-to-go 代价值。在特殊场景下，该方法退化为 Dijkstra 方法。

符号： $ G_{k}^{ \ast} $ ：F 表示最后一步，$ G_{k}^{ \ast} $ 表示从第 k 步到最后一步（F 步）最佳计划下的累计代价

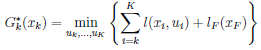
初始条件： $ G_{F}^{ \ast}\left ( x_{F} \right ) = l_{F}\left ( x_{F} \right ) $
结论：

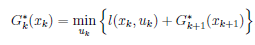
推导过程：

值迭代过程：
$ G_{F}^{ \ast}\rightarrow G_{K}^{ \ast}\rightarrow G_{K-1}^{ \ast}\cdots G_{k}^{ \ast}\rightarrow G_{k-1}^{ \ast}\rightarrow\cdots G_{2}^{ \ast}\rightarrow G_{1}^{ \ast} $

时间复杂度： $ O\left ( K\left | X \right |\left | U \right | \right ) $

离散最优规划标准定义$L\left ( \pi _{K} \right ) = \sum_{k=1}^{K}l(x_{k},u_{k}) + l_{F}(x_{F})$，该时间复杂度为 $ O\left | U \right |^K $，通过引入动态规划，极大降低了复杂度。

举例：

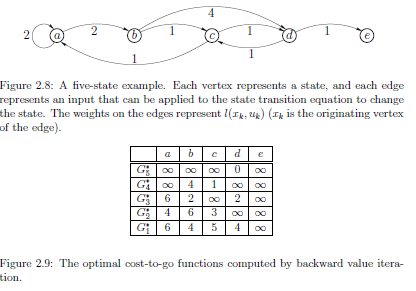
最优cost-to-go
如上图，a 列 $ G_{1}^{ \ast} $ 的值 $G_{1}^{ \ast}\left ( a \right ) $ 代表了 5 步定步长最优规划的累计代价为 6 。那么如何体现动态规划思想降低时间复杂度呢？
当计算 $ G_{4}^{ \ast} $ 的值时，只有 b 和 c 可以只经过 1 步到达 d，再经过1 步到达目标 e，因此只有$G_{4}^{ \ast}\left ( b \right )$、$G_{4}^{ \ast}\left ( c \right )$为有限值。再计算 $G_{3}^{ \ast}$ 的值时，只有经过 b 和 c 的路径才可能经过 5 步到达目标 e，因此缩小了考虑的范围，具体程序表现为选择到达下一顶点的最小累计代价的行为。

那么，得到了最佳cost-to-go的表，如何提取最佳计划（或路径）？
一种解决方案是为每个顶点存储最优 $G_{n}^{ \ast}$所对应的行为，因此这样需要的内存复杂度为 $O(K\left | X \right |)$ 。

正向值迭代

为什么需要正向值迭代？正向值和反向值迭代的区别是什么？
反向：
反向值迭代可以同时找到各顶点到目标顶点的最优计划；
反向值迭代需要目标顶点是确定不变的；
正向：
正向值迭代可以用来找到从初始顶点出发到其他各顶点的最优计划；
正向值迭代需要初始顶点是确定不变的；

基本思想：在状态空间中迭代计算最优的 cost-to-come 代价值。
下图为上例，根据正向值迭代得到的最优 cost-to-come 代价值表。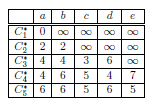
最优cost-to-come

最优不定步长规划

离散不定长最优规划

$L\left ( \pi _{K} \right ) = \sum_{k=1}^{K}l(x_{k},u_{k}) + l_{F}(x_{F})$

通过引入代价项Lf(xf)这一技巧，将离散可行规划中的约束转换为优化问题代价函数中的一项。

对比最优定长规划问题和最优不定步长规划的区别，主要在于终止条件的设置。
定长问题：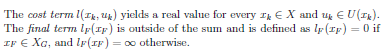

不定步长：允许不同长度的计划
不定长问题

在最优不定步长问题中，从$x_{I}$到$X_{G}$的两步计划$\left ( u_{1}, u_{2}\right )$等效于从$x_{I}$到$X_{G}$的五步计划$\left ( u_{1}, u_{2},u_{T},u_{T},u_{T}\right )$，因此最优定长规划中的正(反)向值迭代优化方法都可以扩展用于最优不定步长问题中。