最开始思考这两种有没有关系的时候也是偶然，，受到启发：雅可比行列式有什么意义呢，为什么对于像

的式子为什么要其后乘上一个雅可比行列式的绝对值呢？在说我的想法之前，我想可能要先提一下一些预备知识，大致有：

1. 什么是雅可比行列式
2. 雅可比行列式的作用
3. 什么是直观图
4. 什么是斜二测画法

1.什么是雅可比行列式

在高等教育出版社，同济大学版的《高等数学.下》第152页有如下定理：

定理 设

在

平面上的闭区域D上连续，若变换

将

平面上的闭区域

变成

平面上的D，且满足：

(1)

在

上具有一阶连续偏导数；

(2)在

上雅可比式

(3)变换

上面这个式子也就是二重积分换元公式：

其中雅可比式

2.雅可比行列式的作用

如顶图，在二维的情况下对于坐标面

下的一小块

在 坐标面

中有唯一的

下图从雅可比矩阵来说明雅可比的变化情况，下面这个解释

，在

坐标系中，

和

可以看成是小矩形的长和宽，它们相互垂直，

可以简单的理解为两个标量相乘求面积，用来代替

，但是在

坐标系中，

和

相互垂直，但是

代表的是一个平行四边形的两条边，显然它们并不一定垂直，那么在

坐标系中我们不能讲

简单的两个标量相乘，而是应该理解为两个向量叉乘所得向量的模（面积）：两边取模，

3.4什么是直观图.什么是斜二测画法

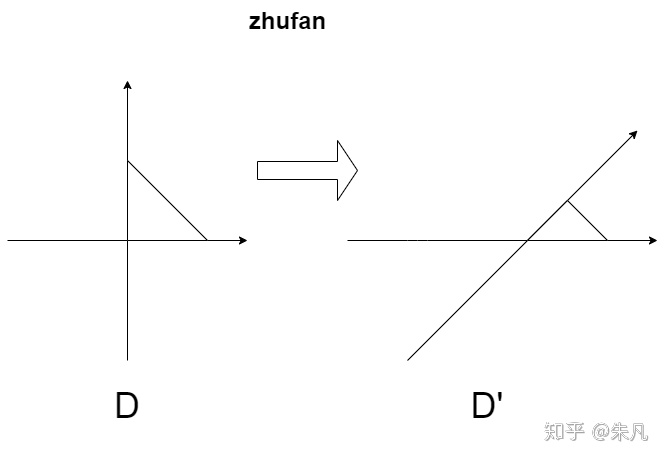
一个物体，从直观看上去的图形，叫做直观图。画直观图的方法叫做斜二测画法。画直观图的方法叫做斜二测画法，规则是

（1）在已知图像中取互相垂直的x轴和y轴，两轴相交于点O，画直观图时，画出相应的x′ 轴和y′ 轴，两轴相交于O′，且使∠x′O′y′=45° 或135° ，它们确定的平面表示水平面。

（2）已知图形中平行于x轴或y轴的线段，在直观图中分别画出平行于x′ 轴和y′ 轴的线段。

如顶图，在二维的情况下对于坐标面 在直观图中长度保持不变，平行于y轴的线段长度变成原来 的一半。^[2]

有了上面的了解之后，我考虑两者的相似点：

首先：变换T:

是一对一的，同样的也可以在斜二测画的时候把上面对应小块看成是一一对应的，对于变换

我们通过上面有

也就是每一个小块的面积比

就是

，同样的对于斜二测画法，如果把斜二测画法(简记成“斜二”)看成一种变换，

设原三角形直角边为a，有

,

类似地，也有

也存在一个比值。

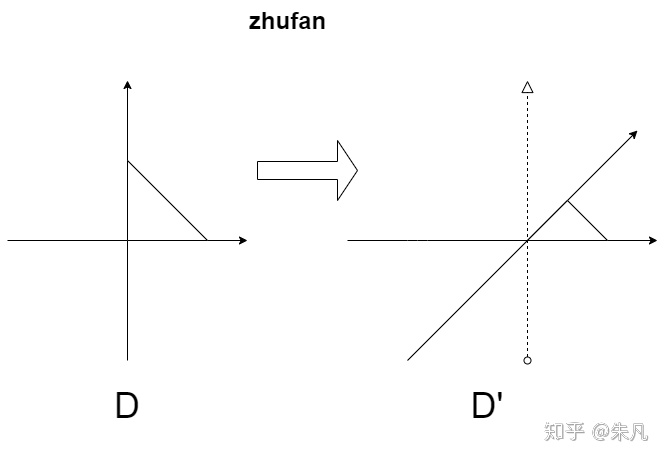
为了方便观察，再加上一条本不存在的纵轴

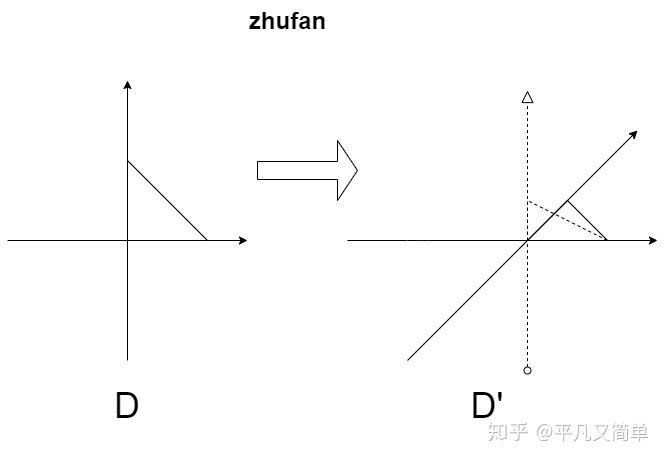
以上只是我的一些想法，水平有限，在认知层面上，对微积分以及雅可比行列式的理解可能有些错误，欢迎指出讨论。也欢迎点赞支持。因为可能存在的认知错误特加上虚拟创作，希望不要对别人产生误导。

封面（图一）来自：雅可比行列式的意义及推导

绘图工具：好用的在线工具

参考

1. ^二重积分和雅可比行列式_SallenKey https://blog.csdn.net/xiaoyink/article/details/88432372
2. ^直观图_百度百科 https://baike.baidu.com/item/%E7%9B%B4%E8%A7%82%E5%9B%BE