From: http://blog.csdn.net/touch_2011/article/details/6767673

1、序言

这是《漫谈经典排序算法系列》第一篇，该篇从最简单的选择排序算法谈起，由浅入深的详细解析两种选择排序算法的过程及性能比较。逐步揭露选择排序的本质及其基本思想。

各种排序算法的解析请参考如下：

《漫谈经典排序算法:一、从简单选择排序到堆排序的深度解析》

《漫谈经典排序算法:二、各种插入排序解析及性能比较》

《漫谈经典排序算法:三、冒泡排序 && 快速排序》

《漫谈经典排序算法:四、归并排序》

《漫谈经典排序算法:五、线性时间排序(计数、基数、桶排序)》

《漫谈经典排序算法:六、各种排序算法总结》 

        注：为了叙述方便，本文以及源代码中均不考虑A[0],默认下标从1开始。

2、提出问题

     （1）简单选择排序和堆排序的基本思想是什么？

     （2）选择排序的本质是什么？

       相信看完这篇文章，读者一定可以找到答案。 

3、漫谈简单选择排序

        3.1 从一个简单问题谈起

        给定待排序序列A[ 1.....n ]，选择出A中最小的记录（也可以理解为求一个无序数组A中的最小的元素）。下面给出代码如下：

 

[cpp] view plaincopy

1. <span style="font-size:18px;">    //选择待排序序列a中的最小记录,其下标为index  
2.     for(index=i=1;i<=n;i++){  
3.         if(a[i]<a[index])  
4.             index=i;  
5.     }</span>  

         相信这段代码大家都能看懂，其中A[index]即为要找的最小记录。也许有人要问作者是在写选择排序，干嘛要谈这个简单的问题呢？请不要急，看到后面自然就知道了。

        3.2 简单选择排序的过程

        描述：给定待排序序列A[ 1......n ] ，选择出第i小元素，并和A[i]交换，这就是一趟简单选择排序。

        代码：

[cpp] view plaincopy

1. <span style="font-size:18px;">//简单选择排序  
2. void simpleSelectionSort1(int *a,int n)  
3. {  
4.     int i,j,index;  
5.     //1.进行n-1趟选择，每次选出第i小记录  
6.     for(i=1;i<n;i++){  
7.         index=i;  
8.         //2.选择第i小记录为a[index]  
9.         for(j=i+1;j<=n;j++)  
10.             if(a[j]<a[index])  
11.                 index=j;  
12.         //3.与第i个记录交换  
13.         if(index!=i){  
14.             a[i]=a[i]+a[index];  
15.             a[index]=a[i]-a[index];  
16.             a[i]=a[i]-a[index];  
17.         }  
18.     }  
19. }</span>  

        示例：假设给定数组A[1......6]={ 3,5,8,9,1,2 }，我们来分析一下A数组进行选择排序的过程

        第一趟：i=1，index=5， a[1] 和 a[5] 进行交换。得到序列：{ 1,5,8,9,3,2 }

        第二趟：i=2，index=6， a[2] 和 a[6] 进行交换。得到序列：{ 1,2,8,9,3,5 }

        第三趟：i=3，index=5， a[3] 和 a[5] 进行交换。得到序列：{ 1,2,3,9,8,5 }

        第四趟：i=4，index=6， a[3] 和 a[5] 进行交换。得到序列：{ 1,2,3,5,8,9 }

        第五趟：i=5，index=5， 不用交换。得到序列：{ 1,2,3,5,8,9 }

       （6-1）趟选择结束，得到有序序列：{ 1,2,3,5,8,9 }

        3.3 性能分析

容易看出，简单选择排序所需进行记录移动的操作次数较少，这一点上优于冒泡排序，最佳情况下（待排序序列有序）记录移动次数为0，最坏情况下（待排序序列逆序）记录移动次数n-1。外层循环进行了n-1趟选择，第i趟选择要进行n-i次比较。每一趟的时间：n-i次的比较时间+移动记录的时间（为一常数0或1，可以忽略）。总共进行了n-1趟。忽略移动记录的时间，所以总时间为(n-1)*(n-i)=n^2-(i+1)*n+i。时间复杂度为O（n^2）。不管是最坏还是最佳情况下，比较次数都是一样的，所以简单选择排序平均时间、最坏情况、最佳情况 时间复杂度都为O（n^2）。同时简单选择排序是一种稳定的原地排序算法。当然稳定性还是要看具体的代码，在此就不做深究。          

3.4 简单选择排序引发的思考    

第一趟排序后：{ 1,5,8,9,3,2 } ，此时A[ 1 ]已经有序，我们可以把待排序序列缩减到A[ 2......6 ]

第二趟排序后：{ 1,2,8,9,3,5 }，此时A[ 1...2 ]已经有序，我们可以把待排序序列缩减到A[ 3......6 ]

第三趟排序后：{ 1,2,3,9,8,5 }，此时A[ 1...3 ]已经有序，我们可以把待排序序列缩减到A[ 4......6 ]

第四趟排序后：{ 1,2,3,5,8,9 }，此时A[ 1...4 ]已经有序，我们可以把待排序序列缩减到A[ 5......6 ]

第五趟排序后：{ 1,2,3,5,8,9 }，此时A[ 1...5 ]已经有序，我们可以把待排序序列缩减到A[ 6......6 ]

也就是说第i趟后，A[ 1...i ]已经有序，待排序序列缩减为A[ (i+1)...n ]。这是一个待排序序列中记录不断减少的递归过程。也许很多读者已经发现，我们每次都是从待排序序列中选择最小的那个记录然后跟待排序序列的首元素进行交换。于是可以用一个递归函数来进行简单选择排序，代码如下：

 

[cpp] view plaincopy

1. <span style="font-size:18px;">//递归函数进行简单选择排序  
2. void simpleSelectionSort2(int *a,int n)  
3. {  
4.     int index,i;  
5.     if(n==1)  
6.         return;  
7.     //1.选择待排序序列a中的最小记录,其下标为index  
8.     for(index=i=1;i<=n;i++){  
9.         if(a[i]<a[index])  
10.             index=i;  
11.     }  
12.     //2.最小记录与待排序序列首元素进行交换  
13.     if(index!=1){  
14.         a[1]=a[1]+a[index];  
15.         a[index]=a[1]-a[index];  
16.         a[1]=a[1]-a[index];  
17.     }  
18.     //3.待排序序列元素个数减少，递归对剩下的无序序列排序  
19.     simpleSelectionSort2(a+1,n-1);  
20. }</span>  

 

看到这里，不知大家是否还记得上文3.1中谈到的简单的问题。由此可以看出这个简单的问题正是简单选择排序的本质所在。

4、深入堆排序

        4.1 堆排序的引入

       从上文我们知道简单选择排序的时间复杂度为O（n^2），熟悉各种排序算法的朋友都知道，这个时间复杂度是很大的，所以怎样减小简单选择排序的时间复杂度呢？从上文分析中我们知道简单选择排序主要操作是进行关键字的比较，所以怎样减少比较次数就是改进的关键。 简单选择排序中第i趟需要进行n-i次比较，如果我们用到前面已排好

的序列a[1...i-1]是否可以减少比较次数呢？答案是可以的。举个例子来说吧，A、B、C进行比赛，B战胜了A，C战胜了B，那么显然C可以战胜A，C和A就不用比了。正是基于这种思想，有人提出了树形选择排序：对n个记录进行两两比较，然后在（[n/2]向上取整）个较小者之间在进行两两比较，如此重复，直到选出最小记录。但是这种排序算法需要的辅助空间比较多，所以威洛姆斯在1964年提出了另一种选择排序，这就是下面要谈的堆排序。

        4.2 什么是堆

       首先堆是一种数据结构，是一棵完全二叉树且满足性质：所有非叶子结点的值均不大于或均不小于其左、右孩子结点的值，如下是一个堆得示例：

               

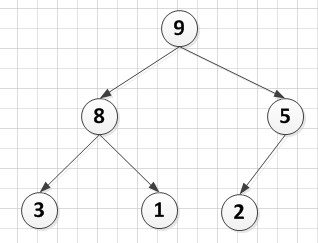
         9>8,9>5;8>3,8>1;5>2   由此发现非叶子结点的值均不小于左右孩子结点的值，所以这是个大顶堆，即堆顶的值是这个堆中最大的一个。

        下面的问题是我们怎么样在计算机中存储这个堆呢？也许有人会想到树的存储，确实，刚看这个堆我也是这么想的。然而事实并非如此，这个堆可以看成是一个一维数组A[6]={9,8,5,3,1,2}，那么相应的这个数组需满足性质：A[i]<=A[2*i] && A[i]<=A[2*i+1] 。其中A[i]对应堆中的非叶子结点，A[2*i]和A[2*i+1]对应于左右孩子结点。并且最后一非叶子结点下标为[n/2]向下取整。

         为什么是[n/2]向下取整呢？在这里我简单的说明一下：设n1表示完全二叉树中有一个孩子的结点，n2表示表示完全二叉树中有两个孩子的结点，d表示非叶子结点的个数，那么总的结点个数：n=n1+2*n2+1。

        （1）当n为奇数时，n1=0，n2=(n-1)/2，d=n2+n1=(n-1)/2

        （2）当n为偶数时，n1=1，n2=n/2-1，d=n2+n1=n/2

          由此可以看出d=[n/2]向下取整.

          注：请大家一定要结合完全二叉树形式的堆以及堆的数组存储形式来看下面的内容，这样才能真正理解堆排序的过程及其本质。

        4.3 筛选法调整堆

        （1）引出：

        现给定一个大顶堆：  即：A[6]={9,8,5,3,1,2}，如果我们稍做破坏，把9跟2互换，同时把a[6]这个结点从堆中去掉，于是得到下面这个完全二叉树：

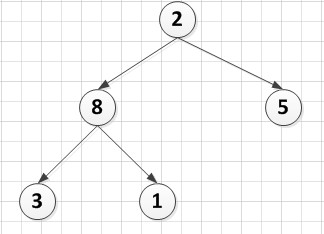        A[5]={2,8,5,3,1}

       显然它不是一个堆，那我们怎么把它调整为一个堆呢？首先观察，我们只是改变了根结点的值，所以根结点左、右子树均是大顶堆。其次思考，既然是根结点可能破坏了堆的性质，那我们就可以把根结点往下沉，让最大值网上浮，即比较根结点和左、右孩子的值，若根结点的值不小于孩子结点的值，说明根结点并没有破坏堆的性质，不用调整；若根结点的值小于左右孩子结点中的任意一个值，则根结点与孩子结点中较大的一个互换，互换之后又可能破坏了左或右子树的堆性质，于是要对子树进行上述调整。这样的一次调整我们称之为一次筛选。

      （2）代码：

       

[cpp] view plaincopy

1. <span style="font-size:18px;">//调整堆，保持大顶堆的性质,参数i指向根结点  
2. void maxHeap(int *a,int n,int i)  
3. {  
4.     //left、right、largest分别指向  
5.     //左孩子、右孩子、{a[i],a[left]}中最大的一个  
6.     int left,right,largest;  
7.     largest=left=2*i;  
8.     if(left>n)  
9.         return;  
10.     right=2*i+1;  
11.     if(right<=n && a[right]>a[left]){  
12.         largest=right;  
13.     }  
14.     if(a[i]<a[largest]){//根结点的值不是最大时,交换a[i]，a[largest]  
15.         a[i]=a[i]+a[largest];  
16.         a[largest]=a[i]-a[largest];  
17.         a[i]=a[i]-a[largest];  
18.         //自上而下调整堆  
19.         maxHeap(a,n,largest);  
20.     }  
21. }</span>  

（3）示例

以这个完全二叉树为例 ：        A[5]={2,8,5,3,1}

第一次筛选：2和8交换

   A[5]={8,2,5,3,1}

第二次筛选：2和3交换

   A[5]={8,3,5,2,1}

筛选完毕，得到大顶堆A[5]={8,3,5,2,1}。

（4）时间代价分析

每一次筛选的过程就是调用一次maxHeap函数，需要的时间是O（1）。那么要执行多少次筛选呢？从上述中可以看出，每一次筛选根结点都往下沉，所以筛选次数不会超过完全二叉树的深度：（[log2n]向下取整+1），其中n为结点个数,2为底数,即时间复杂度为O（log2n）

 为什么n个结点的完全二叉树的深度是([log2n]向下取整+1)呢？这里给出简单的说明：

         深度为h的完全二叉树至多有2^h-1个结点，即2^(h-1)<=n<2^h,推出h-1<=log2n<h;由于h是一个整数，所以h=[log2n]向下取整+1 .

        4.4 建堆

        4.3中叙述了堆的筛选过程，但是给定一个待排序的序列，怎样通过筛选使这个序列满足堆的性质呢？

        给定待排序序列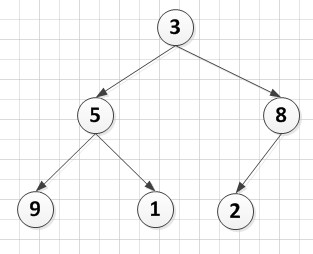  A[6]={3,5,8,9,1,2},怎样使它变成一个堆呢？

        仔细想一想筛选法的前提条件是什么：根结点的左右子树已经是堆。那么这棵树中哪个结点的左右子树是堆呢，很自然的发现是最后一个非叶子结点，所以我们在这里需要自下而上的调整这个完全二叉树。

      （2）代码：

[cpp] view plaincopy

1. <span style="font-size:18px;">//建堆  
2. void creatHeap(int *a,int n)  
3. {  
4.     int i;  
5.     //自下而上调整堆  
6.     for(i=n/2;i>=1;i--)  
7.         maxHeap(a,n,i);  
8. }</span>  

      （3）示例

         待排序序列：  A[6]={3,5,8,9,1,2},     

         以8为根结点调整堆后：因为8>2，此处不进行记录移动操作

         以5为根结点调整堆后：5<9,5跟9互换 

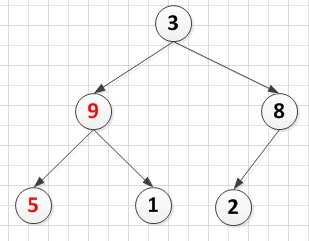             A[6]={3,9,8,5,1,2}

         以3为根结点调整堆后：3<9,3跟9互换

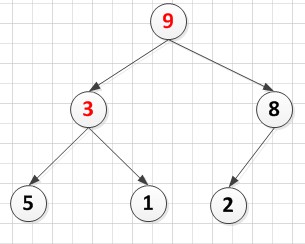            A[6]={9,3,8,5,1,2}

         以9为根的左子树不满足大顶堆的性质，所以以3为跟调整堆,即交换3和5，得A[6]={9,5,8,3,1,2}

        （4）时间代价分析

           从最后一个非叶子结点到第二个结点，总共循环了n/2-1次，每次调用maxHeap函数，4.3中已经分析过maxHeap时间复杂度为O（log2n）。所以建堆的时间复杂度为O（n*log2n）

        4.5 堆排序

      （1）堆排序过程

       也许有的朋友想问：不是讲堆排序吗，为什么不直接讲呢，而是先叙述筛选法和建堆呢？因为筛选法和建堆就构成了堆排序，讲到这里，堆排序可以说是水到渠成。所以一定要理解筛选法和建堆的过程。

       过程描述：1、建堆  2、将堆顶记录和堆中最后一个记录交换  3、筛选法调整堆，堆中记录个数减少一个，重复第2步。整个过程中堆是在不断的缩减。

      （2）代码

[cpp] view plaincopy

1. <span style="font-size:18px;">//堆排序  
2. void heapSort(int *a,int n)  
3. {  
4.     int i;  
5.     creatHeap(a,n);//建堆  
6.     for(i=n;i>=2;i--){  
7.         //堆顶记录和最后一个记录交换  
8.         a[1]=a[1]+a[i];  
9.         a[i]=a[1]-a[i];  
10.         a[1]=a[1]-a[i];  
11.         //堆中记录个数减少一个，筛选法调整堆  
12.         maxHeap(a,i-1,1);  
13.     }  
14. }</span>  

      （3）示例
        0.待排序序列：

         A[6]={3,5,8,9,1,2},  

        1.建堆后（建堆过程参见4.4）：

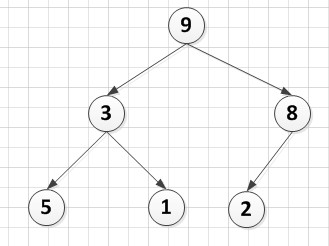        A[6]={9,3,8,5,1,2}

       2.9和2交换，然后把9从堆中去掉后：

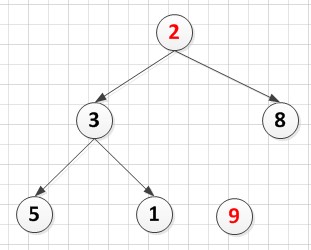         A[6]={2,3,8,5,1,9}

      3.筛选法调整堆A[5]={2,3,8,5,1}后（调整过程参见4.3）：

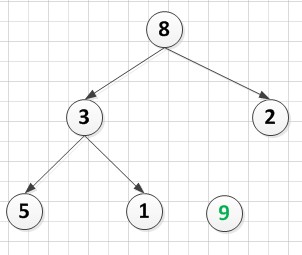       A[6]={8,3,2,5,1,9}

      4.堆顶记录与最后一个记录互换，重复第二步，但是堆顶记录和最后一个记录的值变了

    （4）堆排序性能分析

       堆排序时间=建堆时间+调整堆时间。从上文中知道建堆时间复杂度为O（n*log2n）。筛选法调整堆（maxHeap函数）时间O（log2n），总共循环了n-1次maxHeap函数，所以调整堆时间复杂度为O（n*log2n）。得出堆排序时间复杂度O（n*log2n）。

       熟悉了堆排序的过程后，可以发现堆排序不存在最佳情况，待排序序列是有序或者逆序时，并不对应于堆排序的最佳或最坏情况。且在最坏情况下时间复杂度也是O（n*log2n）。此外堆排序是不稳定的原地排序算法。

        4.6 反思堆排序 ------ 揭开选择排序的本质和基本思想

        叙述到这里，堆排序就叙述完了。不知道大家发现没有，上文中每一个树形的堆边上都有一个数组，其实待排序的整个过程中都是数组元素在不断的交换移动，树形的堆只是能形象的表示这个过程。通过观察这个数组的变化，我们发现了什么呢？

        仔细回想一下筛选法调整堆的过程我们发现，第i次调整堆，其实就是把A中的第i大元素放到首位置A[1]，然后A[1]和A[n-i+1]互换.这样A[(n-i+1)...n]就已经有序，于是又把A[1...n-i]看成一个堆再进行排序，如此重复。

        还记得3.1中提到那个简单的问题（选择出A中最小的记录）吗？调整堆不就是选择出待排序序列中的最大值吗？所以堆排序的本质和选择排序的本质是一样的。选择一个待排序序列中的最小（大）值，这就是选择排序的本质。

        叙述到此，相信大家已然知道开篇提出的两个问题的答案了吧。选择排序的基本思想是：每一趟从n-i+1个记录中选择最小（大）记录和第i（n-i+1）个记录交换。

5、附件

        5.1 附件1

        参考文献：《数据结构》严蔚敏版               《算法导论》第二版

        5.2 附件2

        本文涉及的源代码免积分下载地址：http://download.csdn.net/detail/touch_2011/3594107

        5.3 附件3

        源代码    

        simple_selection_sort.c

[cpp] view plaincopy

1. <span style="font-size:18px;">#include<stdio.h>  
2.   
3. //简单选择排序  
4. void simpleSelectionSort1(int *a,int n)  
5. {  
6.     int i,j,index;  
7.     //1.进行n-1趟选择，每次选出第i小记录  
8.     for(i=1;i<n;i++){  
9.         index=i;  
10.         //2.选择第i小记录为a[index]  
11.         for(j=i+1;j<=n;j++)  
12.             if(a[j]<a[index])  
13.                 index=j;  
14.         //3.与第i个记录交换  
15.         if(index!=i){  
16.             a[i]=a[i]+a[index];  
17.             a[index]=a[i]-a[index];  
18.             a[i]=a[i]-a[index];  
19.         }  
20.     }  
21. }  
22.   
23. //递归函数进行简单选择排序  
24. void simpleSelectionSort2(int *a,int n)  
25. {  
26.     int index,i;  
27.     if(n==1)  
28.         return;  
29.     //1.选择待排序序列a中的最小记录,其下标为index  
30.     for(index=i=1;i<=n;i++){  
31.         if(a[i]<a[index])  
32.             index=i;  
33.     }  
34.     //2.最小记录与待排序序列首元素进行交换  
35.     if(index!=1){  
36.         a[1]=a[1]+a[index];  
37.         a[index]=a[1]-a[index];  
38.         a[1]=a[1]-a[index];  
39.     }  
40.     //3.待排序序列元素个数减少，递归对剩下的无序序列排序  
41.     simpleSelectionSort2(a+1,n-1);  
42. }  
43.   
44.      </span>  

        heap_sort.c

[cpp] view plaincopy

1. <span style="font-size:18px;">#include<stdio.h>  
2.   
3. //调整堆，保持大顶堆的性质,参数i指向根结点  
4. void maxHeap(int *a,int n,int i)  
5. {  
6.     //left、right、largest分别指向  
7.     //左孩子、右孩子、{a[i],a[left]}中最大的一个  
8.     int left,right,largest;  
9.     largest=left=2*i;  
10.     if(left>n)  
11.         return;  
12.     right=2*i+1;  
13.     if(right<=n && a[right]>a[left]){  
14.         largest=right;  
15.     }  
16.     if(a[i]<a[largest]){//根结点的值不是最大时,交换a[i]，a[largest]  
17.         a[i]=a[i]+a[largest];  
18.         a[largest]=a[i]-a[largest];  
19.         a[i]=a[i]-a[largest];  
20.         //自上而下调整堆  
21.         maxHeap(a,n,largest);  
22.     }  
23. }  
24.   
25. //建堆  
26. void creatHeap(int *a,int n)  
27. {  
28.     int i;  
29.     //自下而上调整堆  
30.     for(i=n/2;i>=1;i--)  
31.         maxHeap(a,n,i);  
32. }  
33.   
34. //堆排序  
35. void heapSort(int *a,int n)  
36. {  
37.     int i;  
38.     creatHeap(a,n);//建堆  
39.     for(i=n;i>=2;i--){  
40.         //堆顶记录和最后一个记录交换  
41.         a[1]=a[1]+a[i];  
42.         a[i]=a[1]-a[i];  
43.         a[1]=a[1]-a[i];  
44.         //堆中记录个数减少一个，筛选法调整堆  
45.         maxHeap(a,i-1,1);  
46.     }  
47. }  
48.   
49.  </span>  

        test.c

[cpp] view plaincopy

1. <span style="font-size:18px;">#include<stdio.h>  
2. #include<time.h>  
3. #include"heap_sort.c"  
4. #include"simple_selection_sort.c"  
5.   
6. void main()  
7. {  
8.     int i;  
9.     int a[7]={0,3,5,8,9,1,2};//不考虑a[0]  
10.     simpleSelectionSort1(a,6);  
11.     simpleSelectionSort1(a,6);  
12.     heapSort(a,6);  
13.     for(i=1;i<=6;i++)  
14.         printf("%-4d",a[i]);  
15.     printf("\n");  
16. }  
17. </span>