目录
- 硬知识
- Python代码
- 使用方法
- 串口收集数据
- 椭球拟合
- 验证
STC15F2K60S2 16.384MHz
Keil uVision V5.29.0.0
PK51 Prof.Developers Kit Version:9.60.0.0
Python 3.8.11 (default, Aug 6 2021, 09:57:55) [MSC v.1916 64 bit (AMD64)] :: Anaconda, Inc. on win32
参考资料:
笔记:python读取串口数据并保到本地txt文件 —— 大头工程师笔记
最小二乘法拟合—基本原理 —— 铁头娃-wefly
硬知识
椭球面的标准方程为:
((x−xo)/A)2+((y−yo)/B)2+((z−zo)/C)2=1((x-x_o)/A)^2+((y-y_o)/B)^2+((z-z_o)/C)^2=1((x−xo)/A)2+((y−yo)/B)2+((z−zo)/C)2=1,
需要拟合的参数有
xo,yo,zo,A,B,Cx_o,y_o,z_o,A,B,Cxo,yo,zo,A,B,C
六个,他们分别是椭球的球心坐标和半轴长。
将标准方程写成一般形式为:
x2+ay2+bz2+cx+dy+ez+f=0x^2+ ay^2+ bz^2+cx+dy +ez+f=0x2+ay2+bz2+cx+dy+ez+f=0,
通过对参数a,b,c,d,e、fa,b,c,d,e、fa,b,c,d,e、f的求解间接求出参数xo,yo,zo,A,B,Cx_o,y_o,z_o,A,B,Cxo,yo,zo,A,B,C。
将实测得到的点代入一般形式,可得到对应的误差项,所有点的误差平方和记作
E(a,b,c,d,e,f)=∑i=1Nei(a,b,c,d,e,f)2E(a,b,c,d,e,f) = \sum_{i=1}^{N}e_i(a,b,c,d,e,f)^2E(a,b,c,d,e,f)=∑i=1Nei(a,b,c,d,e,f)2
求偏导数并令其为0:
∂E/∂a=0\partial E/\partial a = 0∂E/∂a=0,
∂E/∂b=0\partial E/\partial b = 0∂E/∂b=0,
∂E/∂c=0\partial E/\partial c = 0∂E/∂c=0,
∂E/∂d=0\partial E/\partial d = 0∂E/∂d=0,
∂E/∂e=0\partial E/\partial e = 0∂E/∂e=0,
∂E/∂f=0\partial E/\partial f = 0∂E/∂f=0
有
(2y4)∗a+(2y2z2)∗b+(2xy2)∗c+(2y3)∗d+(2y2z)∗e+(2y2)∗f+2x2y2=0(2y^4)*a+(2y^2z^2)*b+(2xy^2)*c+(2y^3)*d +(2y^2z)*e+(2y^2)*f+2x^2y^2=0(2y4)∗a+(2y2z2)∗b+(2xy2)∗c+(2y3)∗d+(2y2z)∗e+(2y2)∗f+2x2y2=0
(2y2z2)∗a+(2z4)∗b+(2xz2)∗c+(2yz2)∗d+(2z3)∗e+(2z2)∗f+2x2z2=0(2y^2z^2)*a +(2z^4)*b+(2xz^2)*c +(2yz^2)*d+(2z^3)*e +(2z^2)*f +2x^2z^2=0(2y2z2)∗a+(2z4)∗b+(2xz2)∗c+(2yz2)∗d+(2z3)∗e+(2z2)∗f+2x2z2=0
(2xy2)∗a+(2xz2)∗b+(2x2)∗c+(2xy)∗d+(2xz)∗e+(2x)∗f+2x3=0(2xy^2)*a+(2xz^2)*b+(2x^2)*c+(2xy)*d+(2xz)*e +(2x)*f+2x^3=0(2xy2)∗a+(2xz2)∗b+(2x2)∗c+(2xy)∗d+(2xz)∗e+(2x)∗f+2x3=0
(2y3)∗a+(2yz2)∗b+(2xy)∗c+(2y2)∗d+(2yz)∗e+(2y)∗f+2x2y=0(2y^3)*a +(2yz^2)*b+(2xy)*c+(2y^2)*d+(2yz)*e+(2y)*f+2x^2y=0(2y3)∗a+(2yz2)∗b+(2xy)∗c+(2y2)∗d+(2yz)∗e+(2y)∗f+2x2y=0
(2y2z)∗a+(2z3)∗b+(2xz)∗c+(2yz)∗d+(2z2)∗e+(2z)∗f+2x2z=0(2y^2z)*a+(2z^3)*b+(2xz)*c+(2yz)*d+(2z^2)*e+(2z)*f+2x^2z=0(2y2z)∗a+(2z3)∗b+(2xz)∗c+(2yz)∗d+(2z2)∗e+(2z)∗f+2x2z=0
(2y2)∗a+(2z2)∗b+(2x)∗c+(2y)∗d+(2z)∗e+(2)∗f+2x2=0(2y^2)*a+(2z^2)*b+(2x)*c+(2y)*d+(2z)*e+(2)*f+2x^2=0(2y2)∗a+(2z2)∗b+(2x)∗c+(2y)∗d+(2z)∗e+(2)∗f+2x2=0
解方程组可得a,b,c,d,e,fa,b,c,d,e,fa,b,c,d,e,f,进而可得xo,yo,zo,A,B,Cx_o,y_o,z_o,A,B,Cxo,yo,zo,A,B,C
上面的六个等式中,设参数矩阵为AMatrixA_{Matrix}AMatrix,常数项移至右边为BMatrixB_{Matrix}BMatrix,参数项为x=[a,b,c,d,e,f]Tx=[a,b,c,d,e,f]^Tx=[a,b,c,d,e,f]T
有AMatrix⋅x=BMatrixA_{Matrix}·x=B_{Matrix}AMatrix⋅x=BMatrix
则x=AMatrix−1⋅BMatrixx=A_{Matrix}^{-1}·B_{Matrix}x=AMatrix−1⋅BMatrix
xo=−c/2x_o=-c/2xo=−c/2
yo=−d/(2a)y_o=-d/(2a)yo=−d/(2a)
zo=−e/(2b)z_o=-e/(2b)zo=−e/(2b)
A=xo2+a⋅yo2+b⋅zo2−fA = \sqrt{x_o^2 + a · y_o^2 + b · z_o^2 - f}A=xo2+a⋅yo2+b⋅zo2−f
B=A/aB = A / \sqrt{a}B=A/a
C=A/bC = A / \sqrt{b}C=A/b
Python代码
if not 1: # 0为串口收集数据,1为椭球拟合import serialser = serial.Serial(port='COM8',baudrate=1200,parity=serial.PARITY_NONE, # 校验位stopbits=serial.STOPBITS_ONE, # 停止位bytesize=serial.EIGHTBITS # 数据位)First_Flag = 0while True:data = ser.readline()if First_Flag: # 丢掉第一次的,避免写入半截数据f = open('./Data.txt', 'a')data = data.decode('utf-8')[:-1]f.write(data)f.close()print(data)First_Flag = 1
else:Data_Path = r'./Data.txt'f = open(Data_Path, 'r')X = []Y = []Z = []for _ in f:List = _.replace(",", " ").split()X.append(int(List[0]))Y.append(int(List[1]))Z.append(int(List[2]))f.close()from matplotlib.font_manager import FontPropertiesfrom numpy.linalg import invfrom numpy import arange, zerosfrom math import sqrt, sin, cosfrom matplotlib import pyplot as pltdef dot_Mul(arr1, arr2):return [a * b for a, b in zip(arr1, arr2)]PI = 3.1415926535897932384626433832795# 实测数据f = open(Data_Path, 'r')x = []y = []z = []for _ in f:List = _.replace(",", " ").split()x.append(int(List[0]))y.append(int(List[1]))z.append(int(List[2]))f.close()# 数据总数num_points = len(x)# 一次项均值x_avr = sum(x) / num_pointsy_avr = sum(y) / num_pointsz_avr = sum(z) / num_points# 二次项均值xx_avr = sum(dot_Mul(x, x)) / num_pointsyy_avr = sum(dot_Mul(y, y)) / num_pointszz_avr = sum(dot_Mul(z, z)) / num_pointsxy_avr = sum(dot_Mul(x, y)) / num_pointsxz_avr = sum(dot_Mul(x, z)) / num_pointsyz_avr = sum(dot_Mul(y, z)) / num_points# 三次项均值xxx_avr = sum(dot_Mul(dot_Mul(x, x), x)) / num_pointsxxy_avr = sum(dot_Mul(dot_Mul(x, x), y)) / num_pointsxxz_avr = sum(dot_Mul(dot_Mul(x, x), z)) / num_pointsxyy_avr = sum(dot_Mul(dot_Mul(x, y), y)) / num_pointsxzz_avr = sum(dot_Mul(dot_Mul(x, z), z)) / num_pointsyyy_avr = sum(dot_Mul(dot_Mul(y, y), y)) / num_pointsyyz_avr = sum(dot_Mul(dot_Mul(y, y), z)) / num_pointsyzz_avr = sum(dot_Mul(dot_Mul(y, z), z)) / num_pointszzz_avr = sum(dot_Mul(dot_Mul(z, z), z)) / num_points# 四次项均值yyyy_avr = sum(dot_Mul(dot_Mul(dot_Mul(y, y), y), y)) / num_pointszzzz_avr = sum(dot_Mul(dot_Mul(dot_Mul(z, z), z), z)) / num_pointsxxyy_avr = sum(dot_Mul(dot_Mul(dot_Mul(x, x), y), y)) / num_pointsxxzz_avr = sum(dot_Mul(dot_Mul(dot_Mul(x, x), z), z)) / num_pointsyyzz_avr = sum(dot_Mul(dot_Mul(dot_Mul(y, y), z), z)) / num_points# 系数矩阵A_Matrix = [[yyyy_avr, yyzz_avr, xyy_avr, yyy_avr, yyz_avr, yy_avr],[yyzz_avr, zzzz_avr, xzz_avr, yzz_avr, zzz_avr, zz_avr],[xyy_avr, xzz_avr, xx_avr, xy_avr, xz_avr, x_avr],[yyy_avr, yzz_avr, xy_avr, yy_avr, yz_avr, y_avr],[yyz_avr, zzz_avr, xz_avr, yz_avr, zz_avr, z_avr],[yy_avr, zz_avr, x_avr, y_avr, z_avr, 1]]# 等式右边的常数项矩阵B_Matrix = [[-xxyy_avr], [-xxzz_avr], [-xxx_avr], [-xxy_avr], [-xxz_avr], [-xx_avr]]result = inv(A_Matrix) @ B_Matrixxo = -result[2] / 2 # 拟合出的x坐标yo = -result[3] / (2 * result[0]) # 拟合出的y坐标zo = -result[4] / (2 * result[1]) # 拟合出的z坐标# 拟合出的x方向上的轴半径A = sqrt(xo * xo + result[0] * yo * yo + result[1] * zo * zo - result[5])# 拟合出的y方向上的轴半径B = A / sqrt(result[0])# 拟合出的z方向上的轴半径C = A / sqrt(result[1])ABC_avr = (A + B + C) / 3kA = ABC_avr / AkB = ABC_avr / BkC = ABC_avr / Cxo = xo[0]yo = yo[0]zo = zo[0]print("拟合结果: ")print("xo = ", xo) # 椭球球心x坐标print("yo = ", yo) # 椭球球心y坐标print("zo = ", zo) # 椭球球心z坐标print("A = ", A) # 拟合出的x方向上的轴半径print("B = ", B) # 拟合出的y方向上的轴半径print("C = ", C) # 拟合出的z方向上的轴半径print("kA = ", kA)print("kB = ", kB)print("kC = ", kC)num_alpha = 90num_sita = 45alfa = arange(0, num_alpha) * 1 * PI / num_alphasita = arange(0, num_sita) * 2 * PI / num_sitaX = zeros((num_alpha, num_sita))Y = zeros((num_alpha, num_sita))Z = zeros((num_alpha, num_sita))for i in range(0, num_alpha):for j in range(0, num_sita):X[i, j] = xo + A * sin(alfa[i]) * cos(sita[j])Y[i, j] = yo + B * sin(alfa[i]) * sin(sita[j])Z[i, j] = zo + C * cos(alfa[i])X = [i for arr in X for i in arr]Y = [i for arr in Y for i in arr]Z = [i for arr in Z for i in arr]fig = plt.figure()Font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=20)ax1 = fig.add_subplot(221, projection='3d')ax1.set_title('实测、拟合对比', fontproperties=Font)ax1.scatter3D(X, Y, Z) # 拟合ax1.scatter3D(x, y, z) # 实测ax2 = fig.add_subplot(222)ax2.set_title('x-y投影', fontproperties=Font)ax2.scatter(X, Y)ax2.scatter(x, y)ax3 = fig.add_subplot(223)ax3.set_title('x-z投影', fontproperties=Font)ax3.scatter(X, Z)ax3.scatter(x, z)ax4 = fig.add_subplot(224)ax4.set_title('y-z投影', fontproperties=Font)ax4.scatter(Y, Z)ax4.scatter(y, z)plt.show()
使用方法
HMC5883L、QMC5883L的驱动程序见【51单片机快速入门指南】4.4:I2C 读取HMC5883L / QMC5883L 磁力计
串口收集数据
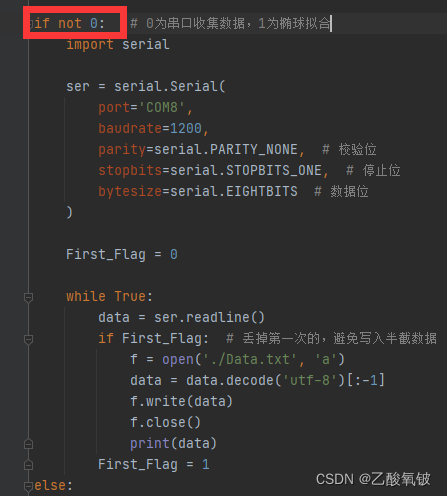
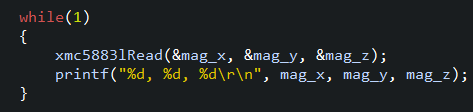
转动板子到各个角度
当觉得收集够时停止脚本
椭球拟合
开始椭球拟合
得到拟合结果:

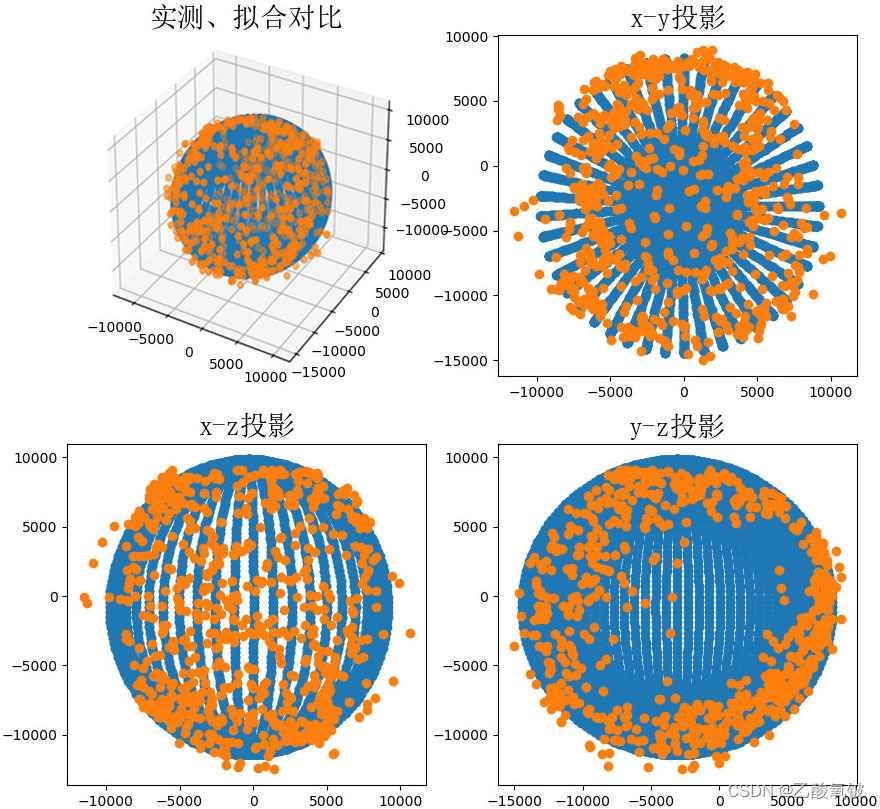
验证
将计算结果用于矫正输出
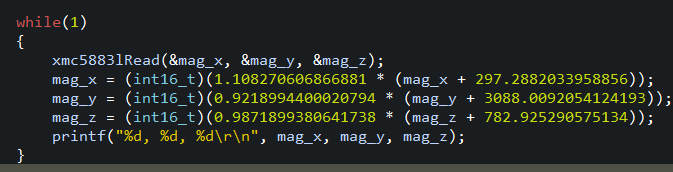
清理掉旧数据后重新收集并拟合,得到如下结果,可见新的球心偏移较未矫正前小,且得到的椭球更接近正球。

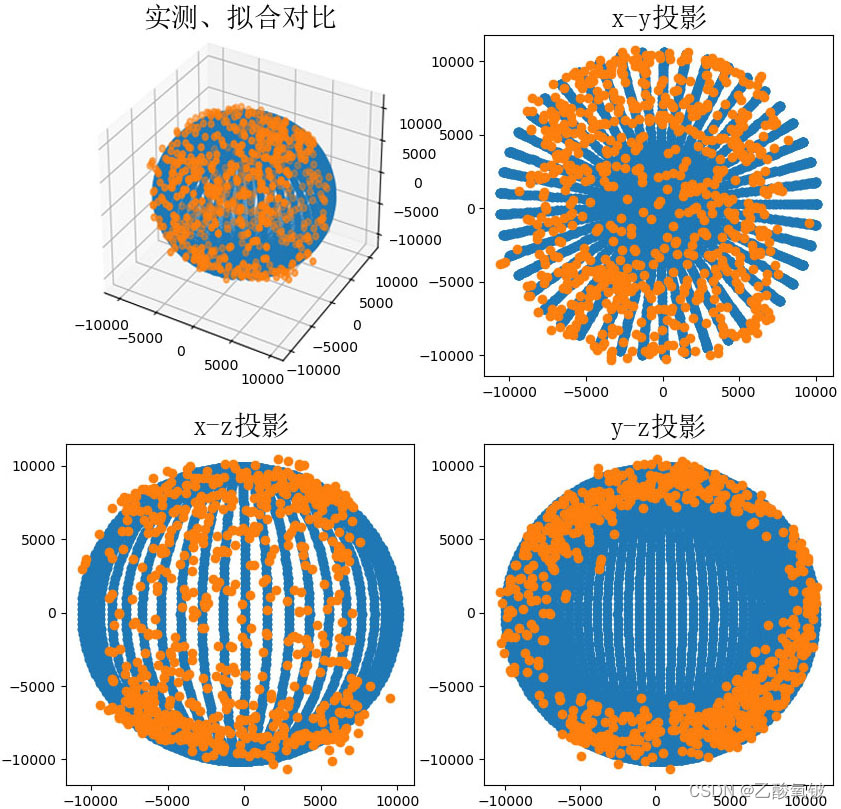

)
![C[泊车管理系统]](http://pic.xiahunao.cn/C[泊车管理系统])




)




)




问题)

