文章目录
- 1 难题
- 2 递归
- 2.1 n的阶层
- 2.2 斐波那契数列的第n项
- 2.3 逆序打印数组
- 3 反转链表
- 4 回顾递归
1 难题
如果不想听我谈学习的过程而注重怎么学习,可以直接跳到第二小节
这个递归的问题是在我刷题的时候遇到的。事实上,我对递归是一窍不通的,第一次学递归是在大二上学期学的数据分析和可视化中遇到了,但是那时候老师叫我们背,所以没怎么注意这个问题。
没注意的问题在后面就开始暴露出来了。在Leetcode刷题的时候,第一次遇见递归是在反转单链表的时候。反转单链表一文可以在每日一题——剑指 Offer24反转链表_尘鱼好美的小屋-CSDN博客中查看。在当时,我用的仅仅是新手都能接受的迭代法。而无法接受思维混乱的递归,但是在解决Leetcode上的另外一道题的时候就开始出问题了,这道题必须用到递归或者栈。
我们学过栈的都知道,栈的本质是递归,这就意味着这个知识点是一个跨不过的坎,我知道我必须面对了。
对于解决这个问题,我首先是看了一下大佬的递归解法剑指 Offer 24. 反转链表(迭代 / 递归,清晰图解) - 反转链表 - 力扣(LeetCode) (leetcode-cn.com)。但是我发现其对于递归的本质没有详细的阐述,反而是只提解法,这对于新手显然十分不友好。我又在看不懂递归的看过来,希望能帮到你! - 反转链表 - 力扣(LeetCode) (leetcode-cn.com)上面看到了另外一个大佬的解法,虽然讲的挺好,但是在单链表反转中又是让人无法接受了,但是至此,我突然脑路一开,发现了一种新思路,我十分愿意和你分享我思考的思路,希望你耐心看完我的文章。
2 递归
大多数讲述递归都是先引出斐波那契数列。实际上,我们无需畏惧递归这个名词,我们先用另外一个词来体会递归,即递推公式,这在我们高中数学中几乎人人学过。在讲述斐波那契数列前,我们来解决一个问题。如何解决用递归实现n的阶层计算?
2.1 n的阶层
完成递归实际上就是三部曲:
- 明确函数目的
- 寻找递归结束条件
- 找出函数的等价关系式
这么说好像太空了,我们来给出一个图,实际上这个图就是递归。

没错,我们可以把俄罗斯套娃看成是递归,也就是说,每一层的娃都是在解决问题,递归的过程是把解决的问题都留在最后,先从外到里一步一步取娃,然后在最里面的娃从里到外解决问题。
现在我们看往例子:如果我们要解决阶层问题,那么结束递归的条件就是一个你知道的数,比如你从5的阶层,那么自然1的阶层是你知道的,那你就可以把1作为结束条件。当然,2你也知道是多少,甚至于更高。我们先用1来作为结束条件:
//结束条件
if(n == 1)
{return 1;
}
那我们接下来就是要写函数等价式了,这实际上是一个创造套娃的过程,从最小的娃开始,和相邻的娃建立联系。也就是说,我们只关注第n个娃和n-1个娃之间的关系,在这个例子中,它们的关系就是f(n) = n*f(n-1)。
等价关系式的寻找在这里看起来十分简单,可实际上,递归最难的就是此步。
接下来我们把上述写成代码,如下所示:
int func(int n)
{if(n == 1)return 1;return n*func(n-1);
}
也可以用2为结束递归条件,如下所示:
int func(int n)
{if(n <= 2)return 2; //2的阶层return n*func(n-1);
}
综上所述,这就是一个最简单的递归了。在下面,我们层层递进,来解决一些实际的问题。
2.2 斐波那契数列的第n项
我们来解决这么一个问题:
斐波那契数列的是这样一个数列:1、1、2、3、5、8、13、21、34…,即第一项 f(1) = 1,第二项 f(2) = 1…,第 n 项目为 f(n) = f(n-1) + f(n-2)。求第 n 项的值是多少。
按照上面的套路,函数实际上是要返回一个第n项的值,所以我们可以这么定义:
int func(int n)
{}
接下来我们要寻找递归结束的条件,根据题意,我们知道f(1) = 1,f(2) = 1… 那么根据我们在最开始讲到的,我们实际上是寻求函数关系等价式,在本题中,如果你采用n = 1作为递归结束条件,那么在函数等价式中(本题已给出)有一个f(n) = f(n-1)+f(n-2),你把2填进去,会出现一个f(0),这样的话越过了f(0)越过了递归结束条件n = 1,会无限死循环下去。
这显然是我们不希望的,所以我们可以用n<=2来作为循环结束条件,这样,f(n)中的n只能填3以上的数字才会出现循环。
综上所述,代码如下所示:
int func(int n){if(n <= 2){return 1;}return func(n-1) + func(n-2)
}
2.3 逆序打印数组
上面的斐波那契数列问题实际上很容易看出函数等价关系式,让我们来一个不那么明显地例子。
我们需要逆序打印一个长度为n的数组。请问如何解决?
也就是说,我们要的是打印一个数组?我们可以这么做:
int func(int arrs[])
{}
接下来我们需要寻找递归结束条件,这个结束的条件就是数组为空,即n = 0就结束。
int func(int arrs[])
{if(n == 0)return false;
}
现在让我们来找函数等价关系,在这里,我们明显要倒序打印,所以首要任务是先打印再倒推,倒推的过程实际上是一个类似于指针移动的过程:n = n-1,所以我们可以写出如下代码:
void func(int arrs[], int n)
{if (n <= 0)return;cout << arrs[n - 1] << endl;return func(arrs, n - 1);
}
3 反转链表
回到我们的主题,我们要解决的最终问题是,如何解决反转链表,乃至解决更多问题,既然要使用递归这个工具乘风破浪,那就先拿这道破题开刀吧。
定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL限制:
0 <= 节点个数 <= 5000
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/fan-zhuan-lian-biao-lcof
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
采用递归,首先要明白函数要干嘛,函数要反转链表并且返回头结点。
//逆置链表函数
ListNode* reverseList(ListNode * head)
{}
但是实际上,我们要实现递归的地方不是在这个逆置函数内,所以我们可以另外写一个递归函数。我们的思路是,分别指定两根指针,一根为pre,一根为cur,反转链表后cur.next = pre。最开始pre一定是空,cur一定是处于head的位置。
//逆置链表函数
ListNode* reverseList(ListNode * head)
{}//递归函数
ListNode* recur(ListNode* cur, ListNode* pre)
{}
接下来找结束条件。最开始pre是空,cur处于head的位置。当递归执行时,最内层的循环是cur快跑到null了。所以结束递归的条件一定是cur->next = NULL。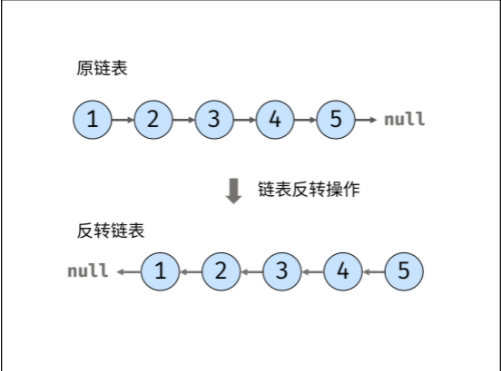
在最内层循环中,我们做的是:改变指针指向,即cur.next = pre。并且在最内层循环是,cur所处位置恰好是逆置后链表头结点所处位置。当递归函数执行完成,返回逆置链表头结点位置。而在逆置链表函数中,仅仅需要调用递归函数并且返回逆置链表头结点位置即可。
class Solution {
public:ListNode* reverseList(ListNode* head) {return recur(head, nullptr); // 调用递归并返回}
private:ListNode* recur(ListNode* cur, ListNode* pre) {if (cur == nullptr) return pre; // 终止条件ListNode* res = recur(cur->next, cur); // 递归后继节点cur->next = pre; // 修改节点引用指向return res; // 返回反转链表的头节点}
};
从套娃的角度来看,我们可以这样做:
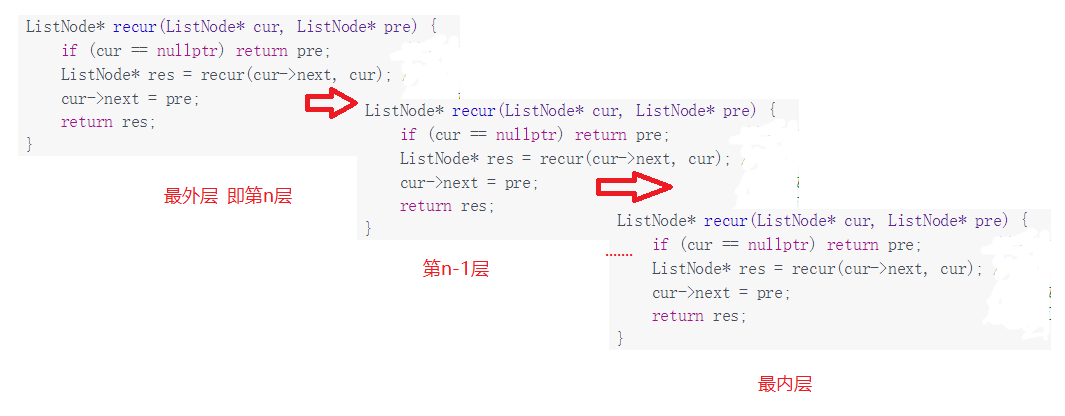
4 回顾递归
递归实际上是一个解决子问题的过程。我们要解决f(n),实际上首先解决f(n-1),要解决f(n-1),实际上要先解决f(n-2),以此类推直至先解决最根本的问题,再回溯整个过程。
递归实际上也是需要优化的,比如f(n) = f(n-1)+f(n-2),如果n = 5,那么n-1 = 4,n-2 = 3,后续在递归的过程中会出现多次f(4)、f(3)等,如果每次都计算,开销挺大,一般可以用某个值来保存,但是这篇文章是针对像我一样的初学者的,我们就偷个懒,放自己一马吧。
好了,彦祖,别太累了,好好消化一下就休息吧。




)
)



)






 下Java开发环境的配置(二)------Tomcat的配置及常见问题)


