背景

今天碰到了代码中的按位与运算，复习一下，先列一个各个进制数据表。

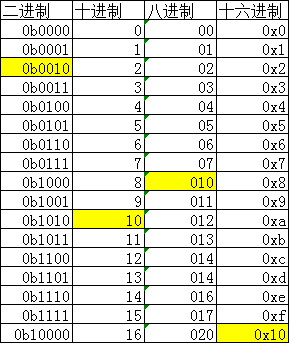
顺便复习一下十进制转二进制的计算方式：

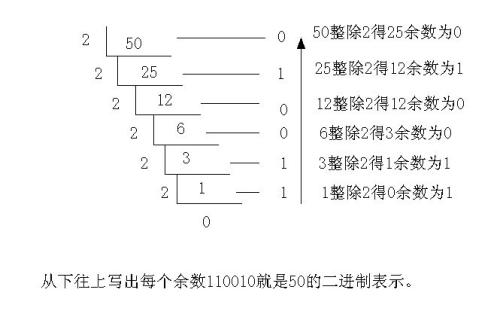
接下来解释下这三个运算符：

&　　按位与，都转为二进制的情况下，同为1则为1，否则为0。

| 　　按位或，都转为二进制的情况下，同为0则为0，否则为1。

^　　按位异或，都转为二进制的情况下，相同为0，不同为1。

示例一

比如有两个数

int x = 5;int y = 11;

在Java代码中做一个计算

System.out.println(x|y);

System.out.println(x&y);

System.out.println(x^y);

计算结果是15， 1 ，14

计算过程分析，都转为二进制进行计算。

x=5 (0101二进制)

y=11(1011二进制)

x|y = 1111 = 15

x&y = 0001 = 1

x^y = 1110 =14

示例二

下面是 java 代码中的一个 if 语句的判断条件：

(8 & 0x10) == 0

这个结果为true，我们来分析一下，这是个按位与运算，都转为二进制的情况下，同为1则为1，否则为0。

十进制数8对应的二进制为1000，十六进制数0x10对应的十进制应该是16，对应的二进制应该是10000。

所以，是对1000和10000这两个二进制数进行按位与运算，同为1则为1，否则为0，计算得到00000，也就是十进制的0。