In this article, I am going to discuss the Gradient Descent algorithm. The next article will be in continuation of this article where I will discuss optimizers in neural networks. For understanding those optimizers it’s important to get a deep understanding of Gradient Descent.

在本文中，我将讨论梯度下降算法。 下一篇文章将是本文的继续，我将在其中讨论神经网络中的优化器。 为了了解这些优化器，对Gradient Descent的深入了解很重要。

内容- (Content-)

1. Gradient Descent
   梯度下降
2. Choice of Learning Rate
   学习率选择
3. Batch Gradient Descent
   批次梯度下降
4. Stochastic Gradient Descent
   随机梯度下降
5. Mini Batch Gradient Descent
   迷你批次梯度下降
6. Conclusion
   结论
7. Credits
   学分

梯度下降- (Gradient Descent-)

Gradient Descent is a first-order iterative optimization algorithm for finding the local minimum of a differentiable function. To get the value of the parameter that will minimize our objective function we iteratively move in the opposite direction of the gradient of that function or in simple terms in each iteration we move a step in direction of steepest descent. The size of each step is determined by a parameter which is called Learning Rate. Gradient Descent is the first-order algorithm because it uses the first-order derivative of the loss function to find minima. Gradient Descent works in space of any number of dimensions.

梯度下降是用于找到可微函数的局部最小值的一阶迭代优化算法。 为了获得将目标函数最小化的参数值，我们迭代该函数的梯度的相反方向，或者在每次迭代中简单地说，我们都沿最陡的下降方向移动一步。 每个步骤的大小由称为学习率的参数确定。 梯度下降法是一阶算法，因为它使用损失函数的一阶导数来找到最小值。 渐变下降可在任意尺寸的空间中工作。

Steps in Gradient Descent-

梯度下降步骤-

1. Initialize the parameters(weights and bias) randomly.
   随机初始化参数(权重和偏差)。
2. Choose the learning rate (‘η’).
   选择学习率('η')。
3. Until convergence repeat this-
   在收敛之前，请重复此操作-

Where ‘wₜ’ is the parameter whose value we have to find, ‘η’ is the learning rate and L represents cost function.

其中“wₜ”是我们必须找到其值的参数，“η”是学习率，L表示成本函数。

By repeat until convergence we mean, repeat until the old value of weight is not approximately equal to its new value ie repeat until the difference between the old value and the new value is very small.

重复直到收敛，我们的意思是，重复直到权重的旧值不等于其新值为止，即重复直到权重的旧值与新值之间的差很小。

Another important thing to be kept in mind is that that all weights need to be updated simultaneously as updating a specific parameter before calculating another one will yield a wrong implementation.

要记住的另一件重要事情是，所有权重都需要同时更新，因为在计算另一个参数之前更新特定参数会产生错误的实现。

学习率选择(η)- (Choice of Learning Rate(η)-)

Choosing an appropriate value of learning is very important because it helps in determining how much we have to descent in each iteration. If the learning rate is too small, the descent will be small and hence there will be a delayed or no convergence on the other hand if the learning rate is too large, then gradient descent will overshoot the minimum point and will ultimately fail to converge.

选择适当的学习价值非常重要，因为它有助于确定我们在每次迭代中必须下降多少。 如果学习速率太小，则下降将很小，因此，如果学习速率太大，则将延迟或没有收敛，则梯度下降将超过最小点，最终将无法收敛。

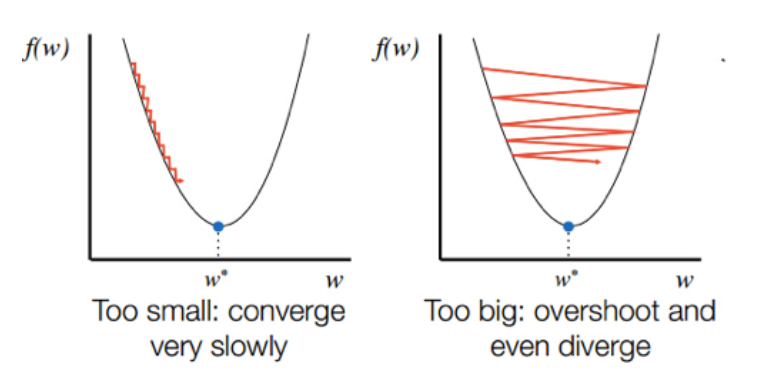
To check this, the best thing is to calculate cost function at each iteration and then plot it with respect to the number of iterations. If cost ever increases we need to decrease the value of the learning rate and if the cost is decreasing at a very slow rate then we need to increase the value of the learning rate.

为了检查这一点，最好的办法是在每次迭代中计算成本函数，然后相对于迭代次数对其进行绘制。 如果成本增加，我们需要降低学习率的值，如果成本以非常缓慢的速度下降，那么我们需要提高学习率的值。

Apart from choosing the right value of learning rate another thing that can be done to optimize gradient descent is to normalize the data to a specific range. For this, we can use any kind of standardization technique like min-max standardization, mean-variance standardization, etc. If we don’t normalize our data then features with a large scale will dominate and gradient descent will take many unnecessary steps.

除了选择正确的学习率值之外，可以做的另一种优化梯度下降的方法是将数据归一化到特定范围。 为此，我们可以使用任何类型的标准化技术，例如最小-最大标准化，均值-方差标准化等。如果不对数据进行标准化，则大规模特征将占主导地位，梯度下降将采取许多不必要的步骤。

Probably in your school mathematics, you must have come across a method of solving optimization problems by computing derivative and then equating it to zero then using the double derivative to check whether that point is the point of minima, maxima, or a saddle point. A question comes in mind why don’t we use that method in machine learning for optimization. The problem with that method is that its time complexity is very high and it will be very slow to implement if our dataset is large. Hence gradient descent is preferred.

可能是在学校数学中，您必须遇到一种解决优化问题的方法，方法是计算导数，然后将其等价为零，然后使用双导数来检查该点是最小值，最大值还是鞍点。 想到一个问题，我们为什么不在机器学习中使用该方法进行优化。 该方法的问题在于它的时间复杂度很高，如果我们的数据集很大，则实现起来将很慢。 因此，梯度下降是优选的。

Gradient descent finds minima of a function. If that function is convex then its local minima will be its global minima. However, if the function is not convex then, in that case, we might reach a saddle point. To prevent this from happening, there are some optimizations that we can apply to Gradient Descent.

梯度下降找到函数的最小值。 如果该函数是凸函数，则其局部最小值将是其全局最小值。 但是，如果函数不是凸函数，那么在这种情况下，我们可能会达到鞍点。 为了防止这种情况的发生，我们可以将某些优化应用于渐变下降。

Limitations of Gradient Descent-

梯度下降的局限性

1. The convergence rate is slow in gradient descent. If we try to speed it by increasing the learning rate then we may overshoot local minima.
   梯度下降时收敛速度慢。 如果我们尝试通过提高学习率来加快速度，那么我们可能会超出局部最小值。
2. If we apply Gradient Descent on a non-convex function we may end up at local minima or a saddle point.
   如果在非凸函数上应用“梯度下降”，则可能会出现在局部最小值或鞍点处。
3. For large datasets, memory consumption will be very high.
   对于大型数据集，内存消耗将非常高。

Gradient Descent is the most common optimization technique used throughout machine learning. Let’s discuss some variations of Gradient Descent.

梯度下降是整个机器学习中最常用的优化技术。 让我们讨论梯度下降的一些变化。

批次梯度下降 (Batch Gradient Descent-)

Batch Gradient Descent is one of the most common versions of Gradient Descent. When we say Gradient Descent in general we are talking about batch gradient descent only. It works by taking all data points available in the dataset to perform computation and update gradients. It works fairly well for a convex function and gives a straight trajectory to the minimum point. However, it is slow and hard to compute for large datasets.

批梯度下降是梯度下降的最常见版本之一。 一般而言，当我们说“梯度下降”时，我们仅在谈论批梯度下降。 它通过获取数据集中所有可用的数据点来执行计算和更新渐变。 它对于凸函数非常有效，并为最小点给出了直线轨迹。 但是，对于大型数据集，它速度慢且难以计算。

Advantages-

优点-

1. Gives a stable trajectory to the minimum point.
   给出最小点的稳定轨迹。
2. Computationally efficient for small datasets.
   对于小型数据集，计算效率高。

Limitations-

局限性

1. Slow for large datasets.
   对于大型数据集，速度较慢。

随机梯度下降 (Stochastic Gradient Descent-)

Stochastic Gradient Descent is a variation of gradient descent which considers only one point at a time to update weights. We will not calculate the total error for whole data in one step instead we will calculate the error of each point and use it to update weights. So basically it increases the number of updates but for each update, less computation will be required. It is based on the assumption that error at each point is additive. Since we are considering just one example at a time the cost will fluctuate and may not necessarily decrease at each step but in the long run, it will decrease. Steps in Stochastic Gradient Descent are-

随机梯度下降是梯度下降的一种变化形式，一次仅考虑一个点来更新权重。 我们不会一步一步地计算整个数据的总误差，而是会计算每个点的误差并使用它来更新权重。 因此，基本上，它增加了更新的数量，但是对于每个更新，将需要较少的计算。 它基于以下假设：每个点的误差都是累加的。 由于我们一次仅考虑一个示例，因此成本会有所波动，并且不一定会在每一步都降低，但从长远来看，它将降低。 随机梯度下降的步骤是-

1. Initialize weights randomly and choose a learning rate.
   随机初始化权重并选择学习率。
2. Repeat until an approximate minimum is obtained-
   重复直到获得近似最小值-

• Randomly shuffle the dataset.
  随机随机播放数据集。
• For each point in the dataset ie if there are m points then-
  对于数据集中的每个点，即如果有m个点，则-

Shuffling the whole dataset is done to reduce variance and to make sure the model remains general and overfit less. By shuffling the data, we ensure that each data point creates an “independent” change on the model, without being biased by the same points before them.

对整个数据集进行混洗以减少方差，并确保模型保持通用性并减少过拟合。 通过对数据进行混排，我们确保每个数据点都在模型上创建“独立”更改，而不会受到之前相同点的影响。

It’s clear from the above image that SGD will go to minima with a lot of fluctuations whereas GD will follow a straight trajectory.

从上图可以清楚地看到，SGD会在波动很大的情况下达到最小值，而GD会遵循一条直线轨迹。

Advantages-

优点-

1. It is easy to fit in memory as only one data point needs to be processed at a time.
   它很容易装入内存，因为一次只需要处理一个数据点。
2. It updates weights more regularly as compared to batch gradient descent and hence it converges faster.
   与批次梯度下降相比，它更定期地更新权重，因此收敛速度更快。
3. It is computationally less expensive than batch gradient descent.
   它在计算上比批量梯度下降便宜。
4. It avoids local minima in case of non-convex function as randomness or noise introduced by stochastic gradient descent allows us to escape local minima and to reach a better minimum.
   它避免了非凸函数的局部最小值，因为随机梯度下降带来的随机性或噪声使我们能够逃脱局部最小值并达到更好的最小值。

Disadvantages-

缺点

1. It is possible that SGD never reaches local minima and may oscillate around it due to a lot of fluctuations in each step.
   由于每个步骤的波动很大，SGD可能永远不会达到局部最小值，并可能在其附近振荡。
2. Each step of SGD is very noisy and gradient descent fluctuates in different directions.
   SGD的每个步骤都非常嘈杂，并且梯度下降沿不同方向波动。

So as discussed above SGD is a better idea than batch GD in case of large datasets but in SGD we have to compromise with accuracy. However, there are various variations of SGD which I will discuss in the next blog using which we can improve SGD to a great extent.

因此，如上所述，在数据集较大的情况下，SGD比批处理GD是更好的主意，但在SGD中，我们必须牺牲准确性。 但是，我将在下一个博客中讨论SGD的各种变化，我们可以在很大程度上利用它们来改进SGD。

迷你批次梯度下降- (Mini Batch Gradient Descent-)

In Mini Batch Gradient Descent instead of using the complete dataset for calculating gradient, we choose only a mini-batch of it. The size of a batch is a hyperparameter and is generally chosen as a multiple of 32 eg 32,64,128,256 etc. Let’s see its equation-

在“小批量梯度下降”中，我们不使用完整的数据集来计算梯度，而是仅选择一个小批量。 批的大小是一个超参数，通常选择为32的倍数，例如32,64,128,256等。让我们看一下它的方程式-

1. Initialize weights randomly and choose a learning rate.
   随机初始化权重并选择学习率。
2. Repeat until convergence-
   重复直到收敛-

Here ‘b’ is batch size.

这里的“ b”是批量大小。

Advantages-

优点-

1. Faster than batch version as it considers only a small batch of data at a time for calculating gradients.
   比批处理版本快，因为它一次只考虑一小批数据来计算梯度。
2. Computationally efficient and easily fits in memory.
   计算效率高，可轻松放入内存。
3. Less prone to overfitting due to noise.
   不太容易因噪音而过拟合。
4. Like SGD, it avoids local minima in case of non-convex function as randomness or noise introduced by mini-batch gradient descent allows us to escape local minima and to reach a better minimum.
   像SGD一样，它避免了非凸函数的局部最小值，因为由小批量梯度下降引起的随机性或噪声使我们能够逃避局部最小值并达到更好的最小值。
5. It can take advantage of vectorization.
   它可以利用矢量化的优势。

Disadvantages-

缺点

1. Like SGD, Due to noise, mini-batch Gradient Descent also may not converge exactly at minima and may oscillate around it.
   像SGD一样，由于噪声的原因，小批量梯度下降可能也无法完全收敛于最小值，并可能在其附近振荡。
2. Although computing each step in mini-batch gradient descent is faster than batch gradient descent due to a small set of points taken into consideration but in the long run, due to noise, it takes more steps to reach minima.
   尽管由于考虑了少量点，所以在小批量梯度下降中计算每个步骤都比批量梯度下降要快，但从长远来看，由于噪声的原因，要达到最小值需要花费更多的步骤。

We can say SGD is also a mini-batch gradient algorithm with a batch size of 1.

我们可以说SGD也是一个小批量梯度算法，批大小为1。

If we particularly compare mini-batch gradient descent and SGD then its clear that SGD is noisier as compared to mini-batch gradient descent and hence it will fluctuate more to reach convergence. However, it is computationally less expensive and with some variations, it can perform much better.

如果我们特别比较小批量梯度下降和SGD，那么很明显SGD与小批量梯度下降相比噪声更大，因此它将波动更大以达到收敛。 但是，它在计算上更便宜，并且有一些变化，它可以执行得更好。

结论- (Conclusion-)

In this article, we discussed Gradient Descent along with its variations and some related terminologies. In the next article, we will discuss optimizers in neural networks.

在本文中，我们讨论了“梯度下降”及其变体和一些相关术语。 在下一篇文章中，我们将讨论神经网络中的优化器。

学分 (Credits-)

1. https://towardsdatascience.com/batch-mini-batch-stochastic-gradient-descent-7a62ecba642a

   https://towardsdatascience.com/batch-mini-batch-stochastic-gradient-descent-7a62ecba642a

2. https://towardsdatascience.com/difference-between-batch-gradient-descent-and-stochastic-gradient-descent-1187f1291aa1

   https://towardsdatascience.com/difference-between-batch-gradient-descent-and-stochastic-gradient-descent-1187f1291aa1

3. https://medium.com/@divakar_239/stochastic-vs-batch-gradient-descent-8820568eada1

   https://medium.com/@divakar_239/stochastic-vs-batch-gradient-descent-8820568eada1

4. https://en.wikipedia.org/wiki/Stochastic_gradient_descent

   https://zh.wikipedia.org/wiki/Stochastic_gradient_descent

5. https://en.wikipedia.org/wiki/Gradient_descent

   https://zh.wikipedia.org/wiki/渐变_下降

That’s all from my side. Thanks for reading this article. Sources for few images used are mentioned rest of them are my creation. Feel free to post comments, suggest corrections and improvements. Connect with me on Linkedin or you can mail me at sahdevkansal02@gmail.com. I look forward to hearing your feedback. Check out my medium profile for more such articles.

这就是我的全部。 感谢您阅读本文。 提到的一些图片来源都是我的创作。 随时发表评论，提出更正和改进建议。 在Linkedin上与我联系，或者您可以通过sahdevkansal02@gmail.com向我发送邮件。 期待收到您的反馈。 查看我的中档，以获取更多此类文章。