Podcasts are a fun way to learn new stuff about the topics you like. Podcast hosts have to find a way to explain complex ideas in simple terms because no one would understand them otherwise 🙂 In this article I present a few episodes to get you going.

播客是一种学习有趣主题的有趣方法。 播客主持人必须找到一种用简单的术语解释复杂想法的方法，因为没人会以其他方式理解它们。🙂在本文中，我将介绍一些情节以助您一臂之力。

In case you’ve missed my previous article about podcasts:

如果您错过了我以前有关播客的文章：

你应该获得博士学位吗 通过部分导数 (Should You Get a Ph.D. by Partially Derivative)

Partially Derivative is hosted by data science super geeks. They talk about the everyday data of the world around us.

数据科学超级极客主持了Partially Derivative。 他们谈论我们周围世界的日常数据。

This episode may be interesting for students who are thinking about pursuing a Ph.D. In this episode, Chris talks about getting a Ph.D. from his personal perspective. He talks about how he wasn’t interested in math when he was young but was more into history. After college, he had enough of school and didn’t intend to pursue a Ph.D. He sent an application to UC Davis and was presented with a challenge. Enjoy listening to his adventure.

对于想攻读博士学位的学生来说， 这一插曲可能会很有趣。 在这一集中，克里斯谈论了获得博士学位的问题。 从他个人的角度来看。 他谈到了他年轻时对数学不感兴趣，但对历史却更加感兴趣。 大学毕业后，他受够了学业，不打算攻读博士学位。 他向加州大学戴维斯分校发送了申请，但面临挑战。 喜欢听他的冒险。

Tim, a two time Ph.D. dropout and a data scientist living in North Carolina, has a website dedicated to this topic: SHOULD I GET A PH.D.?

蒂姆(Tim)，有两次博士学位。 辍学和居住在北卡罗来纳州的数据科学家，有一个专门讨论这个主题的网站： 我应该获得博士学位吗？

Let the adventure begin…

让冒险开始……

线性引数的核技巧和支持向量机 (The Kernel Trick and Support Vector Machines by Linear Digressions)

Katie and Ben explore machine learning and data science through interesting (and often very unusual) applications.

凯蒂(Katie)和本(Ben)通过有趣的(通常是非常不寻常的)应用程序探索机器学习和数据科学。

In this episode, Katie and Ben explain what is the kernel trick in Support Vector Machines (SVM). I really like the simple explanation of heavy machinery behind SVM. Don’t know what maximum margins classifiers are? Then listen first to supporting episode Maximal Margin Classifiers.

在这一集中，Katie和Ben解释了支持向量机(SVM)中的内核技巧是什么。 我真的很喜欢SVM背后有关重型机械的简单说明。 不知道什么是最大利润率分类器？ 然后，首先收听辅助剧集《 最大边际分类器》 。

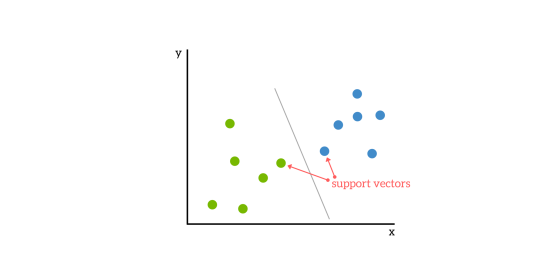
A Maximum Margin Classifier tries to find a line (a decision boundary) between the left and right side so that it maximizes the margin. The line is called a hyperplane because usually there are more 2 dimensions involved. The decision boundary is between support vectors.

最大保证金分类器尝试在左侧和右侧之间找到一条线(决策边界)，以使保证金最大化。 该线称为超平面，因为通常涉及更多的二维。 决策边界在支持向量之间。

什么是内核技巧？ (What is the kernel trick?)

When you have 3 points in a 2-dimensional space, you can arrange points in a way, that they cannot be separated by a line. You can always separate them by putting them in 3 dimensions. One way to introduce a new dimension is to calculate the distance from the origin:

当您在二维空间中有3个点时，可以按某种方式排列点，使它们不能用线隔开。 您始终可以通过将它们分成3维来分离它们。 引入新尺寸的一种方法是计算距原点的距离：

z = x^2 + y^2

This will push points farther from the origin more than the ones closer to the origin. Let’s look at a video below. This also makes a linear classifier non-linear, because it maps the boundary to less dimensional space.

这将使离原点更远的点比靠近原点的点更多。 让我们看下面的视频。 这也使线性分类器成为非线性，因为它将边界映射到较小的空间。

When there are more dimensions than the samples, we can always separate the points with a hyperplane — this is the main idea behind SVM. The polynomial kernel is one of the commonly used kernels with SVM (the most common is Radial basis function). The 2nd-degree polynomial kernel looks for all cross-terms between two features — useful when we would like to model interactions.

当尺寸大于样本时，我们总是可以使用超平面将点分开-这是SVM的主要思想。 多项式内核是支持SVM的常用内核之一(最常见的是Radial基函数)。 2阶多项式内核会寻找两个特征之间的所有交叉项，这在我们希望对交互进行建模时很有用。

What is the kernel tricks? Popcorn that joined the army and they’ve made him a kernel

什么是内核技巧？ 爆米花加入了军队，他们使他成为内核

怀疑论者的AI决策 (AI Decision-Making by Data Skeptic)

The Data Skeptic Podcast features interviews and discussion of topics related to data science, statistics and machine learning.

数据怀疑播客提供有关数据科学，统计和机器学习相关主题的访谈和讨论。

In this episode, Dongho Kim discusses how he and his team at Prowler have been building a platform for autonomous decision making based on probabilistic modeling, reinforcement learning, and game theory. The aim is so that an AI system could make decisions just as good as humans can.

在本集中 ，Dongho Kim讨论了他和他在Prowler的团队如何建立基于概率建模，强化学习和博弈论的自主决策平台。 目的是使AI系统能够做出与人类一样好的决策。

Rather than deep learning, we are most interested in Bayesian processes

而不是深度学习，我们对贝叶斯过程最感兴趣

你走之前 (Before you go)

Follow me on Twitter and join me on my creative journey. I mostly tweet about Data Science.

在Twitter上关注我，并加入我的创意之旅。 我主要在推特上谈论数据科学。

These are a few links that might interest you:

这些链接可能会让您感兴趣：

- Your First Machine Learning Model in the Cloud- AI for Healthcare- Parallels Desktop 50% off- School of Autonomous Systems- Data Science Nanodegree Program- 5 lesser-known pandas tricks- How NOT to write pandas code