As one of the most popular classic machine learning algorithm, the Decision Tree is much more intuitive than the others for its explainability. In one of my previous article, I have introduced the basic idea and mechanism of a Decision Tree model. It demonstrated this machine learning model using an algorithm called ID3, which is one of the most classic ones for training a Decision Tree classification model.

作为最受欢迎的经典机器学习算法之一，决策树在可解释性方面比其他决策树更为直观。 在上一篇文章中，我介绍了决策树模型的基本概念和机制。 它演示了使用称为ID3的算法的机器学习模型，该算法是训练决策树分类模型的最经典模型之一。

If you are not that familiar with Decision Tree, it is highly recommended to check out the above article before reading into this one.

如果您不熟悉决策树，强烈建议您在阅读本文之前先阅读以上文章。

To intuitively understand Decision Trees, it is indeed good to start with ID3. However, it is probably not a good idea to use it in practice. In this article, I’ll introduce a commonly used algorithm to build Decision Tree models — C4.5.

为了直观地理解决策树，从ID3开始确实不错。 但是，在实践中使用它可能不是一个好主意。 在本文中，我将介绍一种用于构建决策树模型的常用算法-C4.5。

经典ID3算法的缺点 (Drawbacks of Classic ID3 Algorithm)

Before we can demonstrate the major drawbacks of the ID3 algorithm, let’s have a look at what are the major building blocks of it. Basically, the important is the Entropy and Information Gain.

在我们证明ID3算法的主要缺点之前，让我们看一下它的主要构成部分。 基本上，重要的是熵和信息增益。

熵回顾 (Recap of Entropy)

Here is the formula of Entropy:

这是熵的公式：

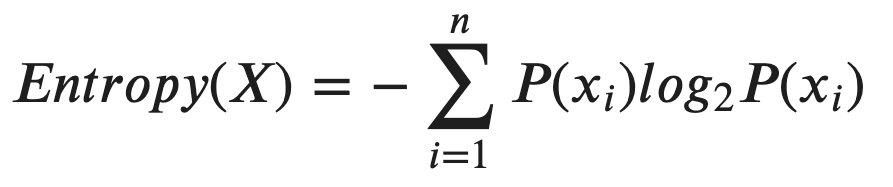
The set “X” is everything in the set of the node, and “xᵢ” refers to the specific decision of each sample. Therefore, “P(xᵢ)” is the probability of the set to be made with a certain decision.

集合“ X ”是节点集合中的所有内容，而“ x ”是指每个样本的特定决策。 因此，“ P(xᵢ) ”是通过确定的决定进行集合的概率。

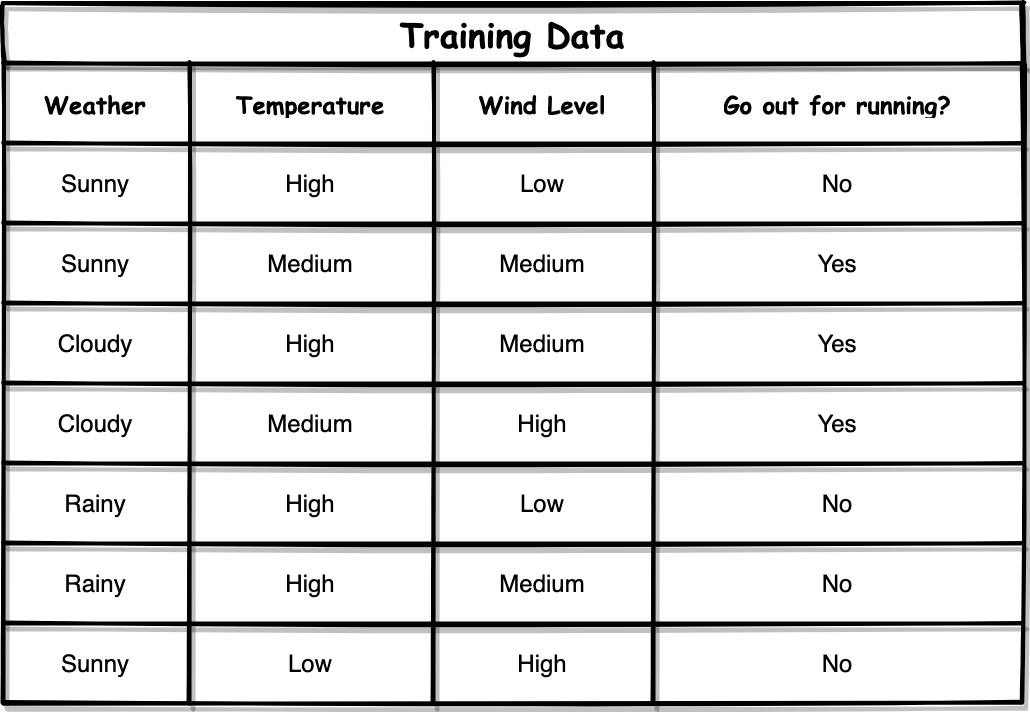
Let’s use the same training dataset as an example. Suppose that we have an internal node in our decision tree with “weather = rainy”. It is can be seen that the final decisions are both “No”. Then, we can easily calculate the entropy of this node as follows:

让我们以相同的训练数据集为例。 假设我们的决策树中有一个内部节点，其“天气=下雨天”。 可以看出，最终决定都是“否”。 然后，我们可以轻松地计算出该节点的熵，如下所示：

Basically, the probability of being “No” is 2/2 = 1, whereas the probability of being “Yes” is 0/2 = 0.

基本上，“否”的概率为2/2 = 1，而“是”的概率为0/2 = 0。

信息获取回顾 (Recap of Information Gain)

On top of the concept of Entropy, we can calculate the Information Gain, which is the basic criterion to decide whether a feature should be used as a node to be split.

在熵的概念之上，我们可以计算信息增益，这是决定是否将特征用作要分割的节点的基本标准。

For example, we have three features: “Weather”, “Temperature” and “Wind Level”. When we start to build our Decision Tree using ID3, how can we decide which one of them should be used as the root node?

例如，我们具有三个功能：“天气”，“温度”和“风力等级”。 当我们开始使用ID3构建决策树时，如何确定应将其中一个用作根节点？

ID3 makes use Information Gain as the criterion. The rule is that, select the feature with the maximum Information Gain among all of them. Here is the formula of calculating Information Gain:

ID3以信息增益为标准。 规则是，在所有选项中选择具有最大信息增益的功能。 这是计算信息增益的公式：

where

哪里

• “T” is the parent node and “a” is the set of attributes of “T”
  “ T”是父节点，“ a”是“ T”的属性集
• The notation “|T|” means the size of the set
  表示法“ | T |” 表示集合的大小

Using the same example, when we calculating the Information Gain for “Weather = Rainy”, we also need to take its child nodes’ Entropy into account. Specific derivation and calculating progress can be found in the article that was shared in the introduction.

使用相同的示例，当我们计算“天气=多雨”的信息增益时，我们还需要考虑其子节点的熵。 在引言中共享的文章中可以找到特定的推导和计算进度。

使用信息增益的主要缺点 (Major Drawbacks of Using Information Gain)

The major drawbacks of using Information Gain as the criterion for determining which feature to be used as the root/next node is that it tends to use the feature that has more unique values.

使用信息增益作为确定哪个特征用作根/下一个节点的标准的主要缺点是，它倾向于使用具有更多唯一值的特征。

But why? Let me demonstrate it using an extreme scenario. Let’s say, we have got the training set with one more feature: “Date”.

但为什么？ 让我用一个极端的场景来演示它。 假设，我们为培训设置了另一个功能：“日期”。

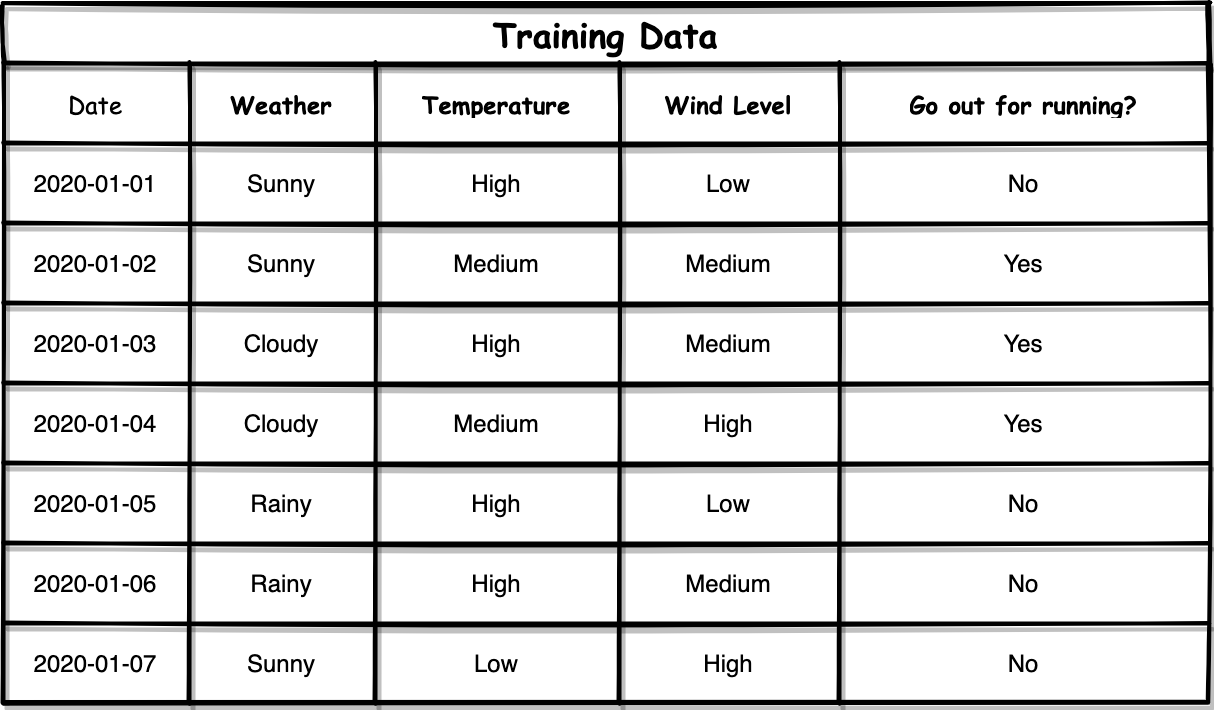
You might say that the feature “Date” should not be considered in this case because it intuitively will not be helpful to decide whether we should go out for running or not. Yes, you’re right. However, practically, we may have much more complicated dataset to be classified, and we may not be able to understand all the features. So, we may not always be able to determine whether a feature does make sense or not. In here, I will just use “Date” as an example.

您可能会说在这种情况下不应考虑“日期”功能，因为它从直觉上对决定我们是否应该运行不起作用没有帮助。 你是对的。 但是，实际上，我们可能要分类的数据集要复杂得多，并且我们可能无法理解所有功能。 因此，我们可能无法始终确定某个功能是否有意义。 在这里，我仅以“日期”为例。

Now, let’s calculate the Information Gain for “Date”. We can start to calculate the entropy for one of the dates, such as “2020–01–01”.

现在，让我们计算“日期”的信息增益。 我们可以开始计算其中一个日期的熵，例如“ 2020-01-01”。

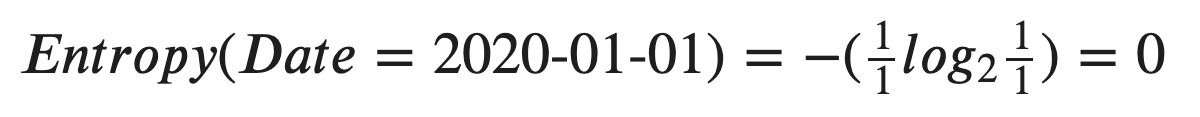
Since there is only 1 row for each date, the final decision must be either “Yes” or “No”. So, the entropy must be 0! In terms of the information theory, it is equivalent to say:

由于每个日期只有一行，因此最终决定必须为“是”或“否”。 因此，熵必须为0！ 就信息论而言，它等同于说：

The date tells us nothing, because the result is just one, which is certain. So, there is no “uncertainty” at all.

日期没有告​​诉我们任何信息，因为结果只是一个，可以肯定。 因此，根本没有“不确定性”。

Similarly, for all the other dates, their entropies are 0, too.

同样，对于所有其他日期，它们的熵也为0。

Now, let’s calculate the entropy for the date itself.

现在，让我们计算日期本身的熵。

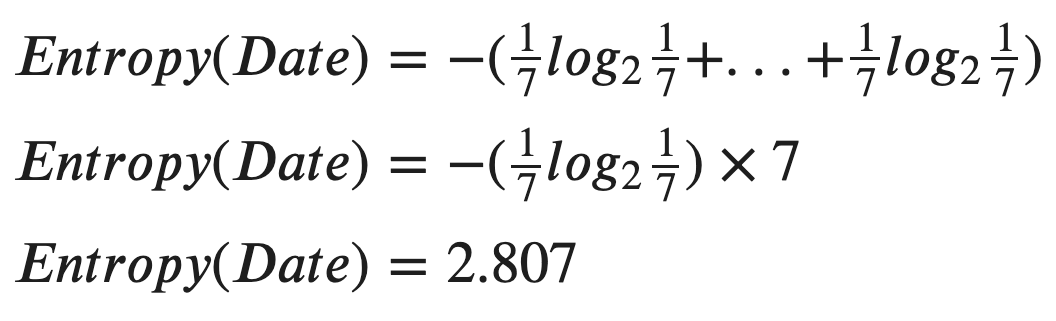
WoW, that is a pretty large number compared to the other features. So, we can calculate the Information Gain of “Date” now.

哇，与其他功能相比，这是一个很大的数目。 因此，我们现在可以计算“日期”的信息增益。

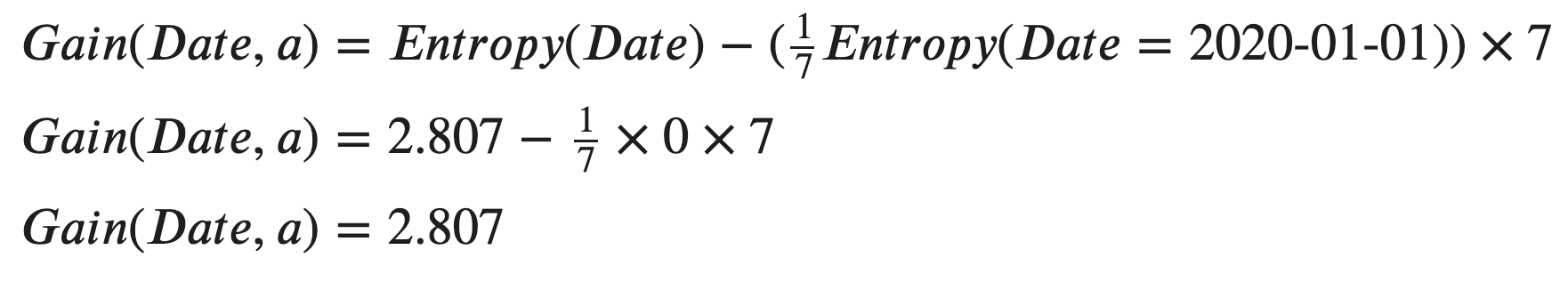
Unsurprisingly, the Information Gain of “Date” is the entropy of itself because all its attribute having entropies that are 0.

毫不奇怪，“日期”的信息增益是其自身的熵，因为其所有属性的熵均为0。

If we calculate the Information Gain for the other three features (you can find details in the article that is linked in the introduction), they are:

如果我们计算其他三个功能的信息增益(您可以在简介中链接的文章中找到详细信息)，则它们是：

• Information Gain of Weather is 0.592
  信息的天气增益为0.592
• Information Gain of Temperature is 0.522
  信息的温度增益为0.522
• Information Gain of Wind Level is 0.306
  风信息增益为0.306

Obviously, the Information Gain of Date is overwhelmingly larger than the others. Also, it can be seen that it will be even larger if the training dataset is larger. After that, don’t forget that the feature “Date” actually does not make sense in deciding whether we should go out for running or not, but it is decided as the “Best” one to be the root node.

显然，最新的信息获取比其他的要大得多。 另外，可以看出，如果训练数据集更大，则该范围将更大。 此后，请不要忘记，“日期”功能在决定是否应该运行时实际上没有意义，而是被确定为“最佳”根节点。

Even funnier, after we decided to use “Date” as our root node, we’re done :)

更有趣的是，在我们决定使用“ Date”作为根节点之后，我们就完成了:)

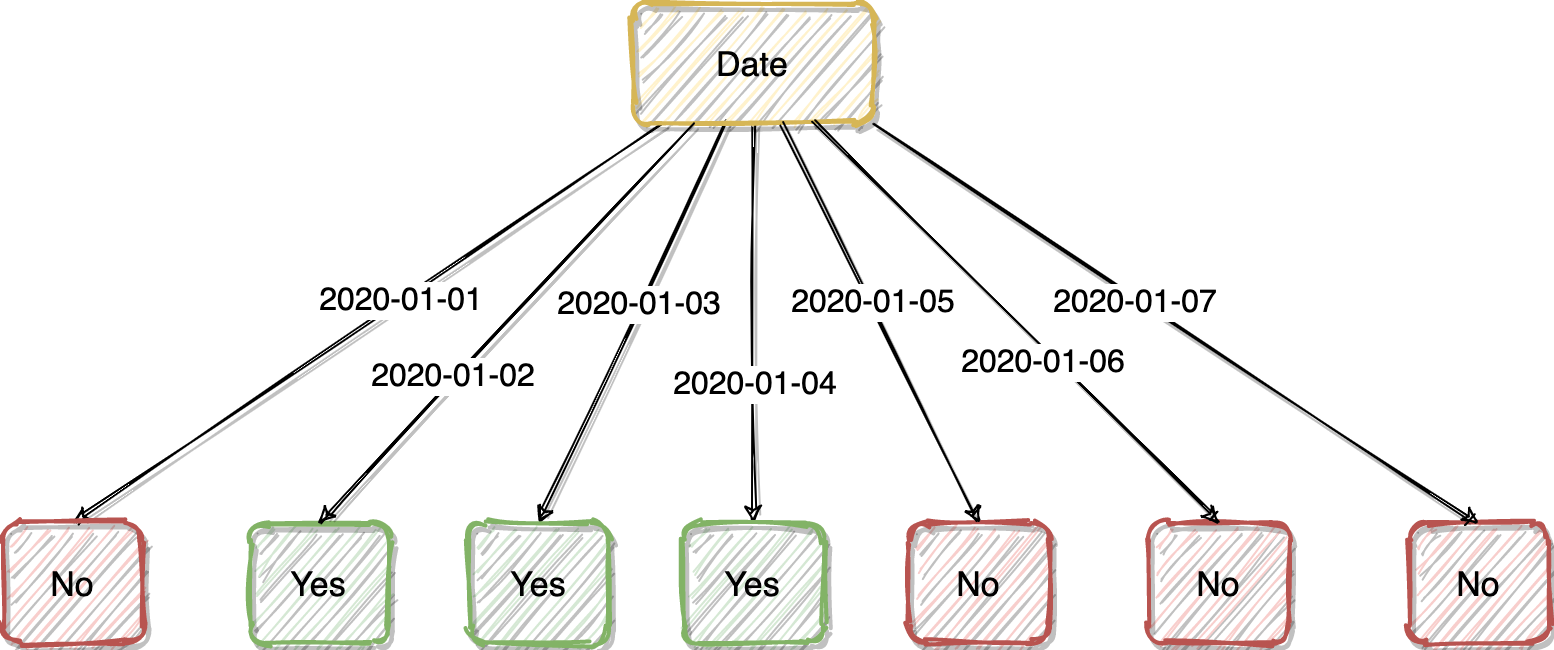
We end up with a Decision Tree as shown above. This is because the feature “Date” is too good. If we use it as the root node, all its attributes will simply tell us whether we should go out for running or not. It is not necessary to have the other features.

我们最终得到了如上所示的决策树。 这是因为功能“日期”太好了。 如果我们将其用作根节点，则其所有属性将简单地告诉我们是否应该运行。 不必具有其他功能。

Yes, you may have a face like this fish at the moment, so do I.

是的，您现在可能有一张像这样的鱼的脸，我也是。

解决信息增益限制 (Fix the Information Gain Limitation)

The easiest fix of the Information Gain limitation that exists in ID3 Algorithm is from another Decision Tree algorithm called C4.5. The basic idea of reducing this issue is to use Information Gain Ratio rather than Information Gain.

ID3算法中存在的信息增益限制的最简单解决方法来自另一种称为C4.5的决策树算法。 减少此问题的基本思想是使用信息增益比而不是信息增益。

Specifically, Information Gain Ratio is simply adding a penalty on the Information Gain by dividing with the entropy of the parent node.

具体而言，信息增益比只是通过除以父节点的熵来对信息增益添加惩罚。

In other words,

换一种说法，

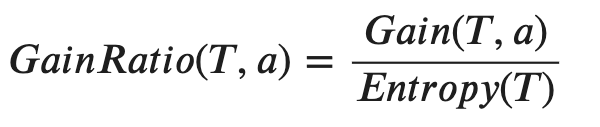
Therefore, if we’re using C4.5 rather than ID3, the Information Gain Ratio of the feature “Date” will be as follows.

因此，如果我们使用的是C4.5而不是ID3，则“日期”功能的信息增益比如下。

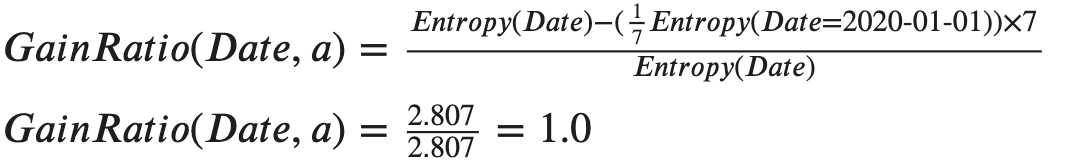
Well, it is indeed still the largest one compared to the other features, but don’t forget that we are really using an extreme example where each attribute value of the feature “Date” will have only one row. In practice, Information Gain Ratio will be quite enough to avoid most of the scenarios that Information Gain will cause bias.

嗯，与其他功能相比，它确实仍然是最大的功能，但是请不要忘记，我们确实使用了一个极端的示例，其中“ Date”功能的每个属性值将只有一行。 实际上，信息增益比率将足以避免大多数情况下信息增益会引起偏差。

C4.5的其他改进 (Other Improvements of C4.5)

In my opinion, using Information Gain Ratio is the most significant improvement from ID3 to C4.5. Nevertheless, there are more improvements in C4.5 that you should know.

我认为，使用信息增益比率是从ID3到C4.5的最大改进。 但是，您应该知道C4.5还有更多改进。

PEP(悲观错误修剪) (PEP (Pessimistic Error Pruning))

If you are not familiar with the concept “Pruning” of Decision Tree, again, you may need to check out my previous article that is attached in the introduction of this article.

如果您不熟悉决策树的“修剪”概念，则可能需要查看本文简介中附带的我以前的文章。

PEP is another significant improvement in C4.5. Specifically, it will prune the tree in a top-down manner. For every internal node, the algorithm will calculate its error rate. Then, try to prune this branch to compare the error rate before and after the pruning. So, it is decided whether we should reserve this branch.

PEP是C4.5的另一个重大改进。 具体来说，它将以自顶向下的方式修剪树。 对于每个内部节点，算法将计算其错误率。 然后，尝试修剪此分支以比较修剪前后的错误率。 因此，决定是否应保留此分支。

Some characteristics of PEP:

PEP的一些特征：

1. It is one of the Post-Pruning methods.
   它是修剪后的方法之一。
2. It prunes the tree without the dependency of a validation dataset.
   它修剪树而不依赖验证数据集。
3. Usually quite good to avoid overfitting, and consequently improve the performance in classifying unknown data.
   通常很好避免过度拟合，因此提高了对未知数据进行分类的性能。

离散连续特征 (Discretising the Continuous Features)

C4.5 supports continuous values. So, we are not limited to have “Low”, “Medium” and “High” such categorical values. Instead, C4.5 will automatically detect the thresholds of the continuous value that can generate the maximum Information Gain Ratio and then split the node using this threshold.

C4.5支持连续值。 因此，我们不限于具有“低”，“中”和“高”这样的分类值。 取而代之的是，C4.5将自动检测可产生最大信息增益比的连续值的阈值，然后使用该阈值拆分节点。

摘要 (Summary)

In this article, I have illustrated why ID3 is not ideal. The major reason is that the criterion it uses — Information Gain — might significantly bias to those features have larger numbers of distinct values.

在本文中，我已说明了为什么ID3不理想。 主要原因是它使用的标准-信息增益-可能会严重偏向那些具有大量不同值的功能。

The solution has been given in another Decision Tree algorithm called C4.5. It evolves the Information Gain to Information Gain Ratio that will reduce the impact of large numbers of distinct values of the attributes.

该解决方案已在另一种称为C4.5的决策树算法中给出。 它改进了信息增益与信息增益之比，从而减少了属性的大量不同值的影响。

Again, if you feel that you need more context and basic knowledge about Decision Trees, please check out my previous article.

同样，如果您觉得需要更多有关决策树的知识和基础知识，请查阅我以前的文章。