一、判别分析
判别分析是一种分类技术,其通过一个已知类别的“训练样本”来建立判别准则,并通过预测变量来为未知类别的数据进行分类。根据判别的模型分为线性判别和非线性判别,线性判别中根据判别准则又分为Fisher判别,Bayes判别和距离判别。本文介绍最基础的Fisher判别,又称线性判别,R中可用MASS包内的lda()函数进行。
注:线性判别的基础假设是数据服从正态分布
1.1 协差阵齐性检验
进行线性判别分析之前需要进行协差阵齐性检验,通过协差阵齐性检验的数据才可以进行线性判别。若未通过协差阵齐性检验,可以进行二次判别,R中可以进行二次判别的函数是MASS包内的qda()函数。
进行协差阵检验使用heplots包内的boxM()函数,其使用方法在我的上一个文章也有提到,用法为
- boxM()用法:boxM(formula,data,...)或boxM(Y,group,...)
formula类参数表示为Y~X1+X2...类型,即指定Y为因变量,X1、X2等为自变量。
boxM()中的formula参数通常是 “data~group” 的形式,data是变量,group是分组变量,分组变量通常要先转为因子
另外一种用法中,Y是数据矩阵或数据框,group是指定的分组变量
例1:
一个城市的居民家庭,按其有无割草机可分为两组,有割草机的一组记为,没有的一组记为
,割草机工厂欲判断家庭(26,10)是否将买割草机。
|
|
| ||
|
|
|
|
|
| 20.0 | 9.2 | 25.0 | 9.8 |
| 28.5 | 8.4 | 17.6 | 10.4 |
| 21.6 | 10.8 | 21.6 | 8.6 |
| 20.5 | 10.4 | 14.4 | 10.2 |
| 29.0 | 11.8 | 28.0 | 8.8 |
| 36.7 | 9.6 | 16.4 | 8.8 |
| 36 | 8.8 | 19.8 | 8.0 |
| 27.6 | 11.2 | 22.0 | 9.2 |
| 23.0 | 10.0 | 15.8 | 8.2 |
| 31.0 | 10.4 | 11.0 | 9.4 |
| 17.0 | 11.0 | 17.0 | 7.0 |
| 27.0 | 10.0 | 21.0 | 7.4 |
注:输入数据时通常将相同变量的数据放在一列,并设置分组变量标识每一个观测的类别
> data1=read.csv('Table1.csv')
> head(data1)x1 x2 y
1 20.0 9.2 1
2 28.5 8.4 1
3 21.6 10.8 1
4 20.5 10.4 1
5 29.0 11.8 1
6 36.7 9.6 1
> library(heplots)
> boxM(cbind(x1,x2)~y,data=data1) #formula参数用法Box's M-test for Homogeneity of Covariance Matricesdata: Y
Chi-Sq (approx.) = 0.99346, df = 3, p-value = 0.8028结果显示不同组的协差阵无显著性差异,即通过协差阵齐性检验
1.2 建立判别模型
对通过协差阵齐性检验的训练集数据可以用lda()建立线性判别模型,未通过协差阵检验的训练集数据可以用qda()建立二次线性判别模型。qda()的用法与lda()相同,此处介绍lda()函数
lda()和qda()都是MASS包内的函数
- lda()用法:lda(formula,data,...)或lda(x,grouping,prior=proportions,...)
lda()函数中的formula参数与boxM()函数不同,左侧是分组变量,即groups~x1+x2+...的形式
另一个用法中,x是各个指标变量,grouping指定分组变量,prior指定先验概率。当未指定prior先验概率时,默认以边缘概率作为先验概率,即各水平的观测数占总观测数的比例为先验概率。若在进行判别分析前已经对研究对象有一定了解,知晓各个水平出现的概率,则可以指定proior先验概率,相当于做的是Bayes判别。
另外再提一提CV参数,CV是逻辑值,当CV=T时返回留一法交叉验证的各项列表。其中包括训练集数据各个观测的分类结果和各个观测的后验概率。但是此时lda()返回的是列表而不是模型,并不能用predict()函数进行新数据的预测。
续上例:
> library(MASS)
> model=lda(y~x1+x2,data=data1)
> model
Call:
lda(y ~ x1 + x2, data = data1)Prior probabilities of groups: #先验概率0 1
0.5 0.5 Group means: #各水平均值x1 x2
0 19.13333 8.816667
1 26.49167 10.133333Coefficients of linear discriminants: #线性判别函数的系数LD1
x1 0.1453404
x2 0.7590457
1.3 新数据的判别
建立判别模型后就可以对新数据进行判别了,对新数据的判别用predict()函数,但是在进行判别之前可以用table()函数对训练集数据回代判别模型的分类结果和训练集数据的实际类别做列联表,相当于查看模型的残差
- predict()用法:predict(object,...)
predict()函数的用处很广泛,其用于根据各种模型拟合函数的结果进行预测,参数object就是进行预测时的要用的模型
第二个参数通常是newdata,即进行预测的新数据。newdata需是列表或数据框,而且这个列表或数据框的变量名需要和训练集的变量名相同。
对lda模型,若未指定newdata或newdata指定不规范,则返回的是训练集数据回代模型的结果,包括分类结果、后验概率和线性判别函数值
- table()用法:table(x,y,...)
table()函数用来每个因子水平组合处构建计数的列联表。
在查看lda模型的残差时,通常指定x为训练集数据回代判别模型的分类结果,指定y为训练集数据各个观测的实际类别。这样生成的列联表行列数相同,对角线上的是预测正确的观测数,非对角线上的是预测错误的观测数,可以由此确定模型的判对率或错误率。
续上例:
> table(data1$y,predict(model)$class)0 10 10 21 1 11
#可见24个观测值中,有3个预测错误
#占训练集总观测数的12.5%
> predict(model,newdata=list(x1=26,x2=10))
$class #判断的分类结果
[1] 1
Levels: 0 1$posterior #新数据的后验概率0 1
1 0.1439459 0.8560541$x #新数据的线性判别函数值LD1
1 0.8617716家庭(26,10)的判别结果为1类,即有割草机家庭。那么工厂可以认为这个家庭是欲购买割草机的。
二、聚类分析
聚类分析是将对象的集合分组为由类似的对象组成的多个类的分析过程。本文介绍R中的系统聚类和k均值聚类
2.1 系统聚类
R中的系统聚类方法用hclust()函数实现,但是在此之前需要对数据进行标准化,并且生成距离阵,以距离阵出发进行系统聚类。数据标准化可用scale()函数,生成距离阵用dist()函数
2.1.1 生成距离阵
用scale标准化数据后,生成距离阵需要定义各个样品之间的距离,在dist()函数的method参数可以选择样品距离的定义,下面介绍两个函数的用法
- scale()用法:scale(x,center=TRUE,scale=TRUE)
其中x为数据矩阵或数据框,返回的是一个对每列变量标准化后的矩阵
- dist()用法:dist(x,method="euclidean",diag=FALSE,upper=FALSE,p=2)
x为数据矩阵或数据框,函数返回的是距离阵,在R中的数据类型是dist而不是matrix
参数method指定样品间距离的定义,默认为"euclidean"——欧几里得距离,可选的距离还有
"maximum"——切比雪夫距离
"manhattan"——绝对距离
"canberra"——兰氏距离
"minkowski"——闵可夫斯基距离
"binary"——定性变量的距离
参数diag和upper是逻辑值,当diag=TRUE时给出对角线上的距离,也就是样品到自身的距离;当upper=TRUE时给出上三角的值,距离阵是对称矩阵,对角线上的距离也一定为0,进行系统聚类时这两个参数可以不管。
参数p是当method="minkowski"时,闵可夫斯基距离的阶数,p=1时为绝对距离,p=2时为欧几里得距离,p=+∞时为切比雪夫距离。
例2:
试对下列数据分别用系统聚类法和均值法进行聚类,并对结果进行比较分析
| 序号 | 省份 | 工资性收入 | 家庭性收入 | 财产性收入 | 转移性收入 |
| 1 | 北京 | 4524.25 | 1778.33 | 588.04 | 455.64 |
| 2 | 天津 | 2720.85 | 2626.46 | 152.88 | 79.64 |
| 3 | 河北 | 1293.50 | 1988.58 | 93.74 | 105.81 |
| 4 | 山西 | 1177.94 | 1563.52 | 62.70 | 86.49 |
| 5 | 内蒙古 | 504.46 | 2223.26 | 73.05 | 188.10 |
| 6 | 辽宁 | 1212.20 | 2163.49 | 113.24 | 201.28 |
注:仅展示部份表格
> data2=read.csv('Table_0.csv',encoding='UTF-8')
> rownames(data2)=data2[,1]
> data2=data2[,-1] #处理数据框
> head(data2)工资性收入 家庭性收入 财产性收入 转移性收入
北京 4524.25 1778.33 588.04 455.64
天津 2720.85 2626.46 152.88 79.64
河北 1293.50 1988.58 93.74 105.81
山西 1177.94 1563.52 62.70 86.49
内蒙古 504.46 2223.26 73.05 188.10
辽宁 1212.20 2163.49 113.24 201.28
> st.data2=scale(data2) #数据标准化
> distance2=dist(st.data2) #生成距离阵,存入distance2中2.1.2 进行系统聚类
用hclust()函数进行系统聚类,函数返回聚类结果,我们可以通过查看聚类结果的各个组件得到聚类过程,也会用到plot()或者plclust()函数画出聚类的系谱图、用rect.hclust()函数根据聚类结果将样品划分类别
- hclust()用法:hclust(d,method="complete",...)
d是距离阵,method指定类间距离的定义,默认为"complete"——最长距离法,可选的其他类间距离的定义有
"single"——最短距离法
"median"——中间距离法
"centroid"——重心法
"average"——类平均法
"ward.D"——离差平方和法
等等
聚类完成后,聚类结果的merge组件记录了聚类过程,height组件记录了聚类过程中每次合并的两类间的距离,order组件记录了绘制聚类系谱图的节点次序
merge组件返回的聚类过程,每一行代表一次合并的两类编号,编号为负值表示在原始数据的编号,编号为正值表示在此表中的对应行合并后的类
- rect.hclust()用法:rect.hclust(tree,k=NULL,...)
rect.hclust()用于在系谱图中绘制分类矩形,在同一个矩形内的为一类
通常通过系谱图大致确定分类的个数,rect.hclust()函数中的k是分类个数,tree是hlust()返回的聚类结果。若将rect.hlust()函数的结果赋给某个变量,那么这个变量会存储每个类的样品名(原始数据的行名)
续上例:
> hclu=hclust(distance2,method='centroid') #重心法
> hclu$merge[1:6,] #展示聚类过程的前6步[,1] [,2][1,] -18 -23 #第一次合并的是第18号和第23号样品,形成类1[2,] -4 -12 #第二次合并的是第4号和第12号样品,形成类2[3,] -24 -27[4,] -28 3 #第四次合并的是第28号样品和类3,类3是第3步合并形成的类[5,] -22 1[6,] 2 5 #第六次合并的是类2和类5,形成类6
> hclu2=hclust(distance2) #作为比较,用最远距离法再聚类
> par(mfrow=c(1,2)) #一页多图
> plot(hclu)
> a=rect.hclust(hclu,4) #看系谱图,大致可分为3、4类
> plot(hclu2)
> b=rect.hclust(hclu2,4)
左图为重心法的聚类结果,右图为最远距离法的聚类结果。根据每个类内的样品不宜过多的原则,通常最远距离法的聚类效果更好,最远距离法通俗的理解是,以样品间最远的距离作为类间距离进行合并,合并的两个类中,最远的两个样品的距离都比其他类样品的距离都小,说明这两个类距离足够近,通常更有说服力。
> a #重心法系统聚类的分类结果
[[1]]
浙江 11 [[2]]天津 河北 山西 内蒙古 辽宁 吉林 黑龙江 江苏 安徽 福建 江西 2 3 4 5 6 7 8 10 12 13 14 山东 河南 湖北 湖南 广东 广西 海南 重庆 四川 贵州 云南 15 16 17 18 19 20 21 22 23 24 25 西藏 陕西 甘肃 青海 宁夏 新疆 26 27 28 29 30 31 [[3]]
北京 1 [[4]]
上海 9 > b #最远距离法系统聚类的分类结果
[[1]]
山西 安徽 湖南 广西 重庆 四川 贵州 云南 西藏 陕西 甘肃 青海 宁夏 4 12 18 20 22 23 24 25 26 27 28 29 30 [[2]]天津 河北 内蒙古 辽宁 吉林 黑龙江 江苏 福建 江西 山东 河南 2 3 5 6 7 8 10 13 14 15 16 湖北 广东 海南 新疆 17 19 21 31 [[3]]
上海 9 [[4]]
北京 浙江 1 11 根据最远距离法系统聚类的分类结果,将我国各省、直辖市、自治区的收入水平划分为4个水平,山西、安徽等水平相似,天津、河北等水平相似,上海独成一类,北京、浙江为一类。说明我国西部地区收入水平普遍低于东部地区,其中沿海的北京、浙江的收入水平更高,上海的收入水平最高。
2.2 k均值聚类
系统聚类法的计算过程繁琐,计算量大,当样品量大时需要占用大量计算机内存空间。k均值聚类是一种快速聚类方法,其基本思想是将每一个样品分配给最近中心(均值)的类中。每分配一个样本,聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。
k均值聚类需要将样品随意分成k个初始类,终止条件通常为所有的样品到最近距离的类都是自身所在的类。在R中进行k均值聚类的函数是kmeans(),这个函数需要指定最终分类个数
- kmeans()用法:kmeans(x,centers,iter.max=10,nstart=1,...)
x为数据矩阵或数据框,在进行k均值聚类前也需要对数据进行标准化
centers用于指定最终聚类个数或者初始类的中心,当centers是最终聚类个数时,nstart用于指定初始类的个数。iter.max是最大迭代次数
kmeans()返回的对象具有以下组件:
- cluster——分类结果
- centers——各个类的聚类中心
- totss——总距离平方和
- withinss——各组的组内距离平方和
- tot.withinss——组内距离平方和的合计
- betweenss——组间距离平方和
2.2.1 聚类数目的确定
随着聚类数目的增加,每个组内的距离平方和将会越来越小并趋于0,当聚类数目合适时,组内的距离平方和越小表示分类的效果越好。但是聚类数目不是越大越好,当通常聚类数目增加到一定大小时,每增加一个聚类数目的组内距离平方和减小的程度也会越来越小。因此我们可以画出聚类数目与组内距离平方和合计值的碎石图确定聚类数目。
k均值聚类碎石图的实现如下:
kmeans.screen=function(x,k=15,nstart=1,iter.max=10){twss=numeric()for(i in 1:k){twss[i]=kmeans(x,i,iter.max=iter.max,nstart=nstart)$tot.withinss}plot(1:k,twss,type='b',pch=19,xlab='聚类数目',ylab='组内平方和总计',main='k均值聚类碎石图')
}
聚类数目不宜过多,通常在2~5个之间。当组内平方和总计下降到一个较小的水平,或聚类数目加一时组内平方和总计下降幅度很小时,可以确定聚类数目。
续上例,进行k均值聚类:
> source("kmeans.screen.R") #加载函数
> kmeans.screen(st.data2,nstart=3,iter.max=20)
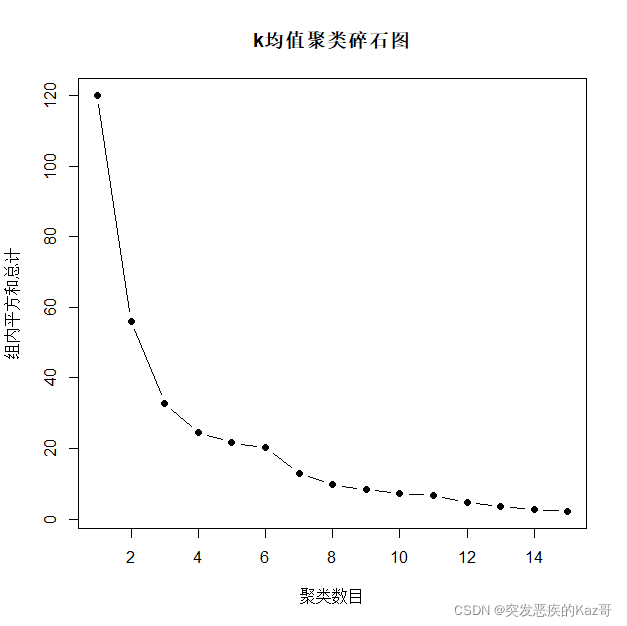
在2~5个间选择聚类数目,结合碎石图可以确定聚类数目为4个,因为4个到5个的组内平方和总计下降幅度很小。
2.2.2 进行k均值聚类
确定好聚类数目就可以进行k均值聚类了,建议画碎石图时的参数和进行k均值聚类时的参数一致,否则碎石图的结果可能会不太可信。通过查看kmeans()返回的cluster模块可以查看分类结果。
kmeans()并没有类似rect.hclust()的将分类结果归类的函数,但是可以编写一个函数实现这一简单的功能:
rect.kmeans=function(kmean){ #kmean是k均值聚类的返回对象clu=kmean$cluster;class=levels(as.factor(clu))numeric.class=as.numeric(class);results=list()for(i in numeric.class){results[[class[i]]]=names(clu)[clu==i]}results
}续上例:
> k.clu=kmeans(st.data2,4,nstart=3,iter.max=20)
> k.clu
K-means clustering with 4 clusters of sizes 14, 5, 10, 2Cluster means:工资性收入 家庭性收入 财产性收入 转移性收入
1 -0.4255246 -0.7442161 -0.4629740 -0.4096606
2 0.9116437 1.0425867 0.4206866 0.4127901
3 -0.4612330 0.7463783 -0.1949991 -0.2512104
4 3.0057285 -1.1288454 3.1640973 3.0917010Clustering vector: #这个是分类结果,也可以通过k.clu$cluster获取北京 天津 河北 山西 内蒙古 辽宁 吉林 黑龙江 上海 江苏 浙江 4 2 3 1 3 3 3 3 4 2 2 安徽 福建 江西 山东 河南 湖北 湖南 广东 广西 海南 重庆 1 2 1 3 3 3 1 2 1 3 1 四川 贵州 云南 西藏 陕西 甘肃 青海 宁夏 新疆 1 1 1 1 1 1 1 1 3 Within cluster sum of squares by cluster:
[1] 5.823392 6.871055 5.067501 6.804320(between_SS / total_SS = 79.5 %)Available components:[1] "cluster" "centers" "totss" "withinss" "tot.withinss"
[6] "betweenss" "size" "iter" "ifault"
> source("rect.kmeans.R") #加载将分类结果归类的函数
> rect.kmeans(k.clu)
$`1`[1] "山西" "安徽" "江西" "湖南" "广西" "重庆" "四川" "贵州" "云南" "西藏" "陕西"
[12] "甘肃" "青海" "宁夏"$`2`
[1] "天津" "江苏" "浙江" "福建" "广东"$`3`[1] "河北" "内蒙古" "辽宁" "吉林" "黑龙江" "山东" "河南" "湖北" [9] "海南" "新疆" $`4`
[1] "北京" "上海"可看到k均值聚类的结果,将我国各省、直辖市、自治区的收入水平分为4类,山西、安徽等地为一类;天津、江苏等地区为一类;河北、内蒙古等地区为一类;北京和上海为一类。
k均值聚类的结果也有说明我国中西部地区与东部地区收入水平低的趋向,相比于系统聚类的结果,k均值聚类对南北方的省份也进行了一定的划分。根据现实各省份总体的发展情况,中西部偏南地区的省份如山西、安徽(第1类)收入水平较低,大部分其余中西部和北方以及海南(第3类)的收入水平次低,而沿海的天津、江苏等省份(第2类)的收入水平较高,作为我国政治中心和经济中心的北京和上海(第4类)的收入水平最高。
三、小结
对线性判别和聚类分析所用到的函数以及应用场景进行总结:
| 判别分析 | |
| 函数 | 应用场景 |
| boxM() | 协差阵齐性检验 |
| lda() | 建立线性判别模型 |
| qda() | 建立二次判别模型 |
| predict() | 模型预测 |
| table() | 做列联表 |
| 系统聚类 | k均值聚类 | ||
| 函数 | 应用场景 | 函数 | 应用场景 |
| scale() | 标准化数据 | scale() | 标准化数据 |
| dist() | 生成距离阵 | kmeans.screen() | 自编,画碎石图 |
| hclust() | 进行系统聚类 | kmeans() | 进行k均值聚类 |
| plot() | 画图,系统聚类中用于画系谱图 | rect.kmeans() | 自编,将k均值聚类的分类结果归类 |
| rect.hclust() | 返回分类结果并在系谱图中圈出 | ||
平台)


![[国家集训队]墨墨的等式](http://pic.xiahunao.cn/[国家集训队]墨墨的等式)








![[Apple开发者帐户帮助]八、管理档案(2)创建临时配置文件(iOS,tvOS,watchOS)...](http://pic.xiahunao.cn/[Apple开发者帐户帮助]八、管理档案(2)创建临时配置文件(iOS,tvOS,watchOS)...)





![[币严区块链]以太坊(ETH)Dapp开发入门教程之宠物商店领养游戏](http://pic.xiahunao.cn/[币严区块链]以太坊(ETH)Dapp开发入门教程之宠物商店领养游戏)
