小王是一家著名高尔夫俱乐部的经理。但是他被雇员数量问题搞得心情十分不好。某些天好像所有人都來玩高尔夫,以至于所有员工都忙的团团转还是应付不过来,而有些天不知道什么原因却一个人也不来,俱乐部为雇员数量浪费了不少资金。
小王的目的是通过下周天气预报寻找什么时候人们会打高尔夫,以适时调整雇员数量。因此首先他必须了解人们决定是否打球的原因。
在2周时间内我们得到以下记录:
天气状况有晴,云和雨;气温用华氏温度表示;相对湿度用百分比;还有有无风。当然还有顾客是不是在这些日子光顾俱乐部。最终他得到了14列5行的数据表格。

决策树模型就被建起来用于解决问题。

决策树是一个有向无环图。根结点代表所有数据。分类树算法可以通过变量outlook,找出最好地解释非独立变量play(打高尔夫的人)的方法。变量outlook的范畴被划分为以下三个组:
晴天,多云天和雨天。
我们得出第一个结论: 如果天气是多云,人们总是选择玩高尔夫,而只有少数很着迷的甚至在雨天也会玩。
接下来我们把晴天组的分为两部分,我们发现顾客不喜欢湿度高于70%的天气。最终我们还发现,如果雨天还有风的话,就不会有人打了。
这就通过分类树给出了一个解决方案。 David(老板)在晴天,潮湿的天气或者刮风的雨天解雇了大部分员工,因为这种天气不会有人打高尔夫。而其他的天气会有很多人打高尔夫,因此可以雇用一些临时员工来工作。
结论是决策树帮助我们把复杂的数据表示转换成相对简单的直观的结构。
公式
熵
算法ID3 , C4.5 和C5.0生成树算法使用熵。这一度量是给予信息学理论中熵的概念。
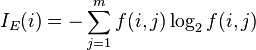
相对于其他数据挖掘算法,决策树在以下几个方面拥有优势:
- 决策树易于理解和实现. 人们在通过解释后都有能力去理解决策树所表达的意义。
- 对于决策树,数据的准备往往是简单或者是不必要的 . 其他的技术往往要求先把数据一般化,比如去掉多余的或者空白的属性。
- 能够同时处理数据型和常规型属性。 其他的技术往往要求数据属性的单一。
- 是一个白盒模型 如果给定一个观察的模型,那么根据所产生的决策树很容易推出相应的逻辑表达式。
- 易于通过静态测试来对模型进行评测。 表示有可能测量该模型的可信度。
- 在相对短的时间内能够对大型数据源做出可行且效果良好的结果。
由决策树扩展为决策图
在决策树中所有从根到叶节点的路径都是通过“与”(AND)运算连接。在决策图中可以使用“或”来连接多于一个的路径。
决策树算法是一种逼近离散函数值的方法。它是一种典型的分类方法,首先对数据进行处理,利用归纳算法生成可读的规则和决策树,然后使用决策对新数据进行分析。本质上决策树是通过一系列规则对数据进行分类的过程。
决策树构造可以分两步进行。第一步,决策树的生成:由训练样本集生成决策树的过程。一般情况下,训练样本数据集是根据实际需要有历史的、有一定综合程度的,用于数据分析处理的数据集。第二步,决策树的剪枝:决策树的剪枝是对上一阶段生成的决策树进行检验、校正和修下的过程,主要是用新的样本数据集(称为测试数据集)中的数据校验决策树生成过程中产生的初步规则,将那些影响预衡准确性的分枝剪除。
java实现代码如下:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 | packagedemo;importjava.util.HashMap;importjava.util.LinkedList;importjava.util.List;importjava.util.Map;importjava.util.Map.Entry;importjava.util.Set;publicclass DicisionTree { publicstatic void main(String[] args) throwsException { System.out.print("脚本之家测试结果:"); String[] attrNames = newString[] { "AGE","INCOME","STUDENT", "CREDIT_RATING"}; // 读取样本集 Map<Object, List<Sample>> samples = readSamples(attrNames); // 生成决策树 Object decisionTree = generateDecisionTree(samples, attrNames); // 输出决策树 outputDecisionTree(decisionTree,0,null); } /** * 读取已分类的样本集,返回Map:分类 -> 属于该分类的样本的列表 */ staticMap<Object, List<Sample>> readSamples(String[] attrNames) { // 样本属性及其所属分类(数组中的最后一个元素为样本所属分类) Object[][] rawData = newObject[][] { {"<30 ","High ","No ","Fair ","0"}, {"<30 ","High ","No ","Excellent","0"}, {"30-40","High ","No ","Fair ","1"}, {">40 ","Medium","No ","Fair ","1"}, {">40 ","Low ","Yes","Fair ","1"}, {">40 ","Low ","Yes","Excellent","0"}, {"30-40","Low ","Yes","Excellent","1"}, {"<30 ","Medium","No ","Fair ","0"}, {"<30 ","Low ","Yes","Fair ","1"}, {">40 ","Medium","Yes","Fair ","1"}, {"<30 ","Medium","Yes","Excellent","1"}, {"30-40","Medium","No ","Excellent","1"}, {"30-40","High ","Yes","Fair ","1"}, {">40 ","Medium","No ","Excellent","0"} }; // 读取样本属性及其所属分类,构造表示样本的Sample对象,并按分类划分样本集 Map<Object, List<Sample>> ret = newHashMap<Object, List<Sample>>(); for(Object[] row : rawData) { Sample sample = newSample(); inti = 0; for(intn = row.length - 1; i < n; i++) sample.setAttribute(attrNames[i], row[i]); sample.setCategory(row[i]); List<Sample> samples = ret.get(row[i]); if(samples == null) { samples = newLinkedList<Sample>(); ret.put(row[i], samples); } samples.add(sample); } returnret; } /** * 构造决策树 */ staticObject generateDecisionTree( Map<Object, List<Sample>> categoryToSamples, String[] attrNames) { // 如果只有一个样本,将该样本所属分类作为新样本的分类 if(categoryToSamples.size() == 1) returncategoryToSamples.keySet().iterator().next(); // 如果没有供决策的属性,则将样本集中具有最多样本的分类作为新样本的分类,即投票选举出分类 if(attrNames.length == 0) { intmax = 0; Object maxCategory = null; for(Entry<Object, List<Sample>> entry : categoryToSamples .entrySet()) { intcur = entry.getValue().size(); if(cur > max) { max = cur; maxCategory = entry.getKey(); } } returnmaxCategory; } // 选取测试属性 Object[] rst = chooseBestTestAttribute(categoryToSamples, attrNames); // 决策树根结点,分支属性为选取的测试属性 Tree tree = newTree(attrNames[(Integer) rst[0]]); // 已用过的测试属性不应再次被选为测试属性 String[] subA = newString[attrNames.length - 1]; for(inti = 0, j = 0; i < attrNames.length; i++) if(i != (Integer) rst[0]) subA[j++] = attrNames[i]; // 根据分支属性生成分支 @SuppressWarnings("unchecked") Map<Object, Map<Object, List<Sample>>> splits = /* NEW LINE */(Map<Object, Map<Object, List<Sample>>>) rst[2]; for (Entry<Object, Map<Object, List<Sample>>> entry : splits.entrySet()) { Object attrValue = entry.getKey(); Map<Object, List<Sample>> split = entry.getValue(); Object child = generateDecisionTree(split, subA); tree.setChild(attrValue, child); } return tree; } /** * 选取最优测试属性。最优是指如果根据选取的测试属性分支,则从各分支确定新样本 * 的分类需要的信息量之和最小,这等价于确定新样本的测试属性获得的信息增益最大 * 返回数组:选取的属性下标、信息量之和、Map(属性值->(分类->样本列表)) */ static Object[] chooseBestTestAttribute( Map<Object, List<Sample>> categoryToSamples, String[] attrNames) { int minIndex = -1; // 最优属性下标 double minValue = Double.MAX_VALUE; // 最小信息量 Map<Object, Map<Object, List<Sample>>> minSplits = null; // 最优分支方案 // 对每一个属性,计算将其作为测试属性的情况下在各分支确定新样本的分类需要的信息量之和,选取最小为最优 for (int attrIndex = 0; attrIndex < attrNames.length; attrIndex++) { int allCount = 0; // 统计样本总数的计数器 // 按当前属性构建Map:属性值->(分类->样本列表) Map<Object, Map<Object, List<Sample>>> curSplits = /* NEW LINE */new HashMap<Object, Map<Object, List<Sample>>>(); for (Entry<Object, List<Sample>> entry : categoryToSamples .entrySet()) { Object category = entry.getKey(); List<Sample> samples = entry.getValue(); for (Sample sample : samples) { Object attrValue = sample .getAttribute(attrNames[attrIndex]); Map<Object, List<Sample>> split = curSplits.get(attrValue); if (split == null) { split = new HashMap<Object, List<Sample>>(); curSplits.put(attrValue, split); } List<Sample> splitSamples = split.get(category); if (splitSamples == null) { splitSamples = new LinkedList<Sample>(); split.put(category, splitSamples); } splitSamples.add(sample); } allCount += samples.size(); } // 计算将当前属性作为测试属性的情况下在各分支确定新样本的分类需要的信息量之和 double curValue = 0.0; // 计数器:累加各分支 for (Map<Object, List<Sample>> splits : curSplits.values()) { double perSplitCount = 0; for (List<Sample> list : splits.values()) perSplitCount += list.size(); // 累计当前分支样本数 double perSplitValue = 0.0; // 计数器:当前分支 for (List<Sample> list : splits.values()) { double p = list.size() / perSplitCount; perSplitValue -= p * (Math.log(p) / Math.log(2)); } curValue += (perSplitCount / allCount) * perSplitValue; } // 选取最小为最优 if (minValue > curValue) { minIndex = attrIndex; minValue = curValue; minSplits = curSplits; } } return new Object[] { minIndex, minValue, minSplits }; } /** * 将决策树输出到标准输出 */ static void outputDecisionTree(Object obj, int level, Object from) { for (int i = 0; i < level; i++) System.out.print("|-----"); if (from != null) System.out.printf("(%s):", from); if (obj instanceof Tree) { Tree tree = (Tree) obj; String attrName = tree.getAttribute(); System.out.printf("[%s = ?]\n", attrName); for (Object attrValue : tree.getAttributeValues()) { Object child = tree.getChild(attrValue); outputDecisionTree(child, level + 1, attrName + " = " + attrValue); } } else { System.out.printf("[CATEGORY = %s]\n", obj); } } /** * 样本,包含多个属性和一个指明样本所属分类的分类值 */ static class Sample { private Map<String, Object> attributes = new HashMap<String, Object>(); private Object category; public Object getAttribute(String name) { return attributes.get(name); } public void setAttribute(String name, Object value) { attributes.put(name, value); } public Object getCategory() { return category; } public void setCategory(Object category) { this.category = category; } public String toString() { return attributes.toString(); } } /** * 决策树(非叶结点),决策树中的每个非叶结点都引导了一棵决策树 * 每个非叶结点包含一个分支属性和多个分支,分支属性的每个值对应一个分支,该分支引导了一棵子决策树 */ staticclass Tree { privateString attribute; privateMap<Object, Object> children = newHashMap<Object, Object>(); publicTree(String attribute) { this.attribute = attribute; } publicString getAttribute() { returnattribute; } publicObject getChild(Object attrValue) { returnchildren.get(attrValue); } publicvoid setChild(Object attrValue, Object child) { children.put(attrValue, child); } publicSet<Object> getAttributeValues() { returnchildren.keySet(); } }} |
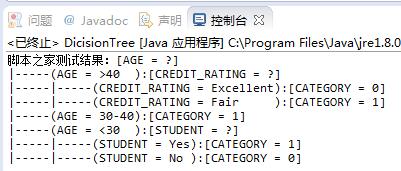
运行结果: