本篇文章主要介绍了Dijkstra迪杰斯特拉算法的C++实现，文章包含两个部分，在第一部分中我会简单介绍迪杰斯特拉算法以及一些个人的理解，第二部分会对C++代码的逻辑进行解释。下面是我已经上传的代码资源，大家有兴趣的可以点击链接下载资源。
迪杰斯特拉算法的C++实现
迪杰斯特拉算法本质上是一个贪心算法，通过不断迭代取得局部最优解的方法，最终找到整体的最优解。迪杰斯特拉算法主要用于在有权图中计算出各节点到初始节点的最短路径。在接下来的分析中我会使用的有权图如下 :
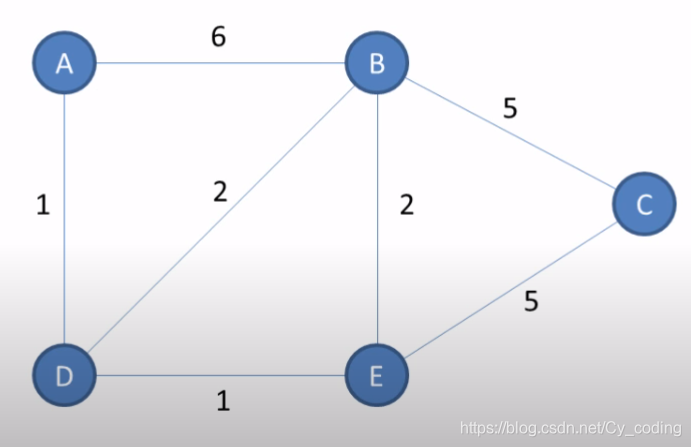
其中，ABCDE就是我们需要遍历的节点，连接节点的弦上的数字表示了两节点之间的"距离"，或称之为权重，消耗。需要注意的几点是 :
- 迪杰斯特拉算法适用的有权图中，节点之间的权重不要求是双向的，即 A-> B的权重和 B->A 的权重不要求相同。换而言之，有权图中节点之间的连接可以是单向的，或者在两个方向权重有所不同的。
- 迪杰斯特拉算法适用的有权图中，节点间连接的权重值不能是负值。
了解了迪杰斯特拉算法的一些注意点之后，我们下面来重点解释算法的实现。之前我们已经提到了，迪杰斯特拉算法多用于解决最短路径问题，对应上述有权图就是计算出所有节点到初始节点的最短距离。在下述例子中，我们默认使用A作为初始节点,目标就是找出所有节点到A的最短距离以及所经过的路径。
首先我们需要两个列表，一个visited列表用于存放已经遍历过其所有邻节点的节点，一个unvisited列表用于存放还未遍历过其所有邻节点的节点。我们会不断地进行迭代运算，直到unvisited列表为空，即所有的节点都已经访问过(遍历过其所有邻节点)。
显然初始状态，visited列表为空[]，unvisited列表中包含所有的节点[A,B,C,D,E]。
然后我们需要一个列表用于记录所有节点到A节点，起始节点之间的最短距离，以及最短路径中该节点之前的节点。
第一步，初始化这个表格 :
显然A到A的距离为0，其余节点到A的距离为未知，初始化为正无穷。
| 节点 | 节点到A的距离 | 最短路径中该节点之前的节点 |
|---|---|---|
| A | 0 | |
| B | ∞\infin∞ | |
| C | ∞\infin∞ | |
| D | ∞\infin∞ | |
| E | ∞\infin∞ |
那么每一次迭代，我们需要做的，就是在unvisited列表中，选择一个到A距离最短的节点，并遍历更新其所有unvisited列表中的邻节点。
例如第一次迭代中，unvisited未访问列表中A节点到A的最短距离最短，那么我们首先就访问A所有unvisited的节点 B 和 D。简单来说，如果通过A访问B比起之前的方式要距离更短，那么我们就更新B到初始点的距离为新的最短距离，并将B之前的节点更新为A。那么在这个例子中，通过A访问B的距离为6，通过A访问D的距离为1，显然距离都比正无穷要小，则更新列表如下 :
| 节点 | 节点到A的距离 | 最短路径中该节点之前的节点 |
|---|---|---|
| A | 0 | |
| B | 6 | A |
| C | ∞\infin∞ | |
| D | 1 | A |
| E | ∞\infin∞ |
同时更新visited列表以及unvisited列表:
visited : [A]
unvisited : [B,C,D,E]
既然未访问列表仍然不为空，我们继续迭代，选择D作为新的访问节点，因为节点D目前到A的距离最短。那么节点D在unvisited列表中的邻节点有 B E，那么我们更新B，E的值和其原来的距离进行对比。 B : 1+2 = 3 < 6 \space E : 1+1 = 2 < ∞\infin∞。
更新列表如下 :
| 节点 | 节点到A的距离 | 最短路径中该节点之前的节点 |
|---|---|---|
| 0 | ||
| B | 1+2 = 3 | D |
| C | ∞\infin∞ | |
| D | 1 | A |
| E | 1+1 = 2 | D |
同时更新visited列表以及unvisited列表:
visited : [A,D]
unvisited : [B,C,E]
我们继续迭代,方法同上。
访问E节点，更新列表 :
| 节点 | 节点到A的距离 | 最短路径中该节点之前的节点 |
|---|---|---|
| 0 | ||
| B | 1+2 = 3 | D |
| C | 1+1+5 = 7 | E |
| 1 | A | |
| E | 1+1 = 2 | D |
同时更新visited列表以及unvisited列表:
visited : [A,D,E]
unvisited : [B,C]
继续访问B，更新列表 :
B的唯一没有访问的邻节点为C，但A> … >B>C 的距离为 3+5=8 >7，因此C到节点A的距离不变。
| 节点 | 节点到A的距离 | 最短路径中该节点之前的节点 |
|---|---|---|
| 0 | ||
| B | 1+2 = 3 | D |
| C | 1+1+5 = 7 | E |
| 1 | A | |
| 1+1 = 2 | D |
同时更新visited列表以及unvisited列表:
visited : [A,D,E,B]
unvisited : [C]
最后我们访问C，列表不变，因为C的所有邻节点都已经访问过了。
最终的结果如下 :
| 节点 | 节点到A的距离 | 最短路径中该节点之前的节点 |
|---|---|---|
| A | 0 | |
| B | 3 | D |
| C | 7 | E |
| D | 1 | A |
| E | 2 | D |
通过迪杰斯特拉算法，我们可以完备地遍历所有有权图中的节点，并在最后返回一个所有节点到初始点的最短距离，以及对应的最短路径的所有节点之前的节点。之后通过不断访问最短路径中该节点之前的节点，我们就可以很简单地还原出最短路径。例如对节点C而言，C之前的节点为E，E之前的节点为D，D之前的节点为A，因此最短路径还原为A > D > E > C。
参考 :
[1] Graph Data Structure 4. Dijkstra’s Shortest Path Algorithm
[2] (熟肉)Dijkstra算法详解，轻松入门——Youtube
