决策树(decision tree)是一个树结构(可以是二叉树或非二叉树)。其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节点,将叶子节点存放的类别作为决策结果。
构建决策树的过程:
关键步骤是分裂属性。所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支,其目标是让各个分裂子集尽可能地“纯”。尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别。分裂属性分为三种不同的情况:
1. 属性是离散值且不要求生成二叉决策树。此时用属性的每一个划分作为一个分支。
2. 属性是离散值且要求生成二叉决策树。此时使用属性划分的一个子集进行测试,按照“属于此子集”和“不属于此子集”分成两个分支。Yes or No.
3. 属性是连续值。此时确定一个值作为分裂点split_point,按照>split_point和<=split_point生成两个分支。
构造决策树的关键性内容是进行属性选择度量,属性选择度量是一种选择分裂准则,是将给定的类标记的训练集合的数据划分D“最好”地分成个体类的启发式分类,它决定了拓扑结构及分裂点split_point的选择。
属性选择度量算法有很多,一般使用自顶向下递归分治法,并采用不回溯的贪心算法。
递归划分方法:
(1) 分区D的所有元祖都属于同一个类;
(2)没有剩余属性可以用来进一步划分元组。在此情况下,使用多数表决。 设计将N转换成树叶,并用D中的多数类标记它。另外,也可以存放节点元组的类分布。
(3)给定的分支没有元组。即有一个分支为空。在这种情况下,用D中的多数类创建一个树叶。
ID3算法
ID3算法的核心思想就是以信息增益度量属性选择,选择分裂后信息增益最大的属性进行分裂。
熵越大,越混乱,越稳定(熵表示混乱程度,越混乱表明越不需要维持,则越稳定;越整齐越需要维持,越不稳定)。
期望信息越小,信息增益越大,从而纯度越高。我们需要找的是最“纯”的特征。
设D为用类别对训练元组进行的划分,则D的熵(entropy)表示为:
其中pi表示第i个类别在整个训练元组中出现的概率,可以用属于此类别元素的数量除以训练元组元素总数量作为估计。熵的实际意义表示是D中元组的类标号所需要的平均信息量。
现在我们假设将训练元组D按属性A进行划分,则A对D划分的期望信息为:
而信息增益即为两者的差值:
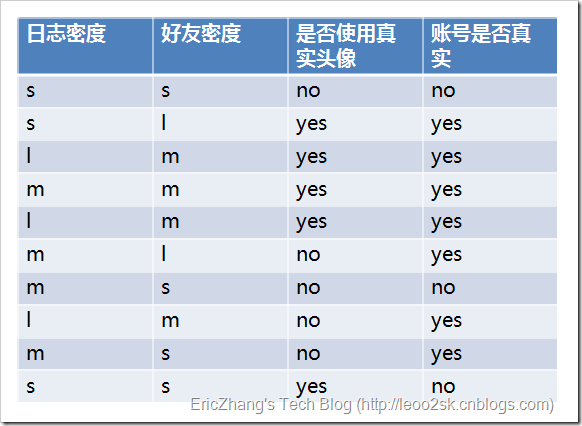
ID3算法就是在每次需要分裂时,计算每个属性的增益率,然后选择增益率最大的属性进行分裂。下面我们继续用SNS社区中不真实账号检测的例子说明如何使用ID3算法构造决策树。为了简单起见,我们假设训练集合包含10个元素:
其中s、m和l分别表示小、中和大。
设L、F、H和R表示日志密度、好友密度、是否使用真实头像和账号是否真实,下面计算各属性的信息增益。
因此日志密度的信息增益是0.276。
用同样方法得到H和F的信息增益分别为0.033和0.553。
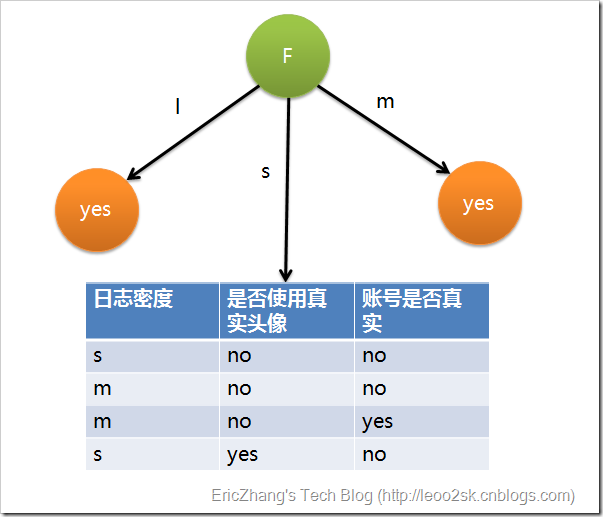
因为F具有最大的信息增益,所以第一次分裂选择F为分裂属性,分裂后的结果如下图表示:
在上图的基础上,再递归使用这个方法计算子节点的分裂属性,最终就可以得到整个决策树。
上面为了简便,将特征属性离散化了,其实日志密度和好友密度都是连续的属性。对于特征属性为连续值,可以如此使用ID3算法:
先将D中元素按照特征属性排序,则每两个相邻元素的中间点可以看做潜在分裂点,从第一个潜在分裂点开始,分裂D并计算两个集合的期望信息,具有最小期望信息的点称为这个属性的最佳分裂点,其信息期望作为此属性的信息期望。
C4.5算法
ID3算法存在一个问题,就是偏向于多值属性,例如,如果存在唯一标识属性ID,则ID3会选择它作为分裂属性,这样虽然使得划分充分纯净,但这种划分对分类几乎毫无用处。ID3的后继算法C4.5使用增益率(gain ratio)的信息增益扩充,试图克服这个偏倚。
C4.5算法实现步骤:1)求“分裂信息” :
2)求熵:
3)划分期望:
4)信息增益:
5)增益率:
C4.5选择具有最大增益率的属性作为分裂属性。
建议参考机械工业出版社《数据挖掘概念与技术》第3版,P213-P220,更容易明白。
——————————————————————————我是华丽丽的分割线——————————————————————————欢迎互相讨论交流,望不吝赐教。















——基础选择器、过滤选择器、表单选择器)

—— 操作DOM元素)

——事件与应用)