【算法训练】DAY1：整数反转

1 前言

题目来源于Leetcode。
在这里插入图片描述

重点：理清逻辑，忽略细节，模仿高手，五毒神掌

2 题目分析

题目很容易理解，先分成两个部分

  • 正数
  • 负数

先解决正数

最开始想到的是

int
char数组
long

唯一增加的就是，先判断整数是多少位。

之后再判断溢出

然后解决负数
先使用一个bool变量保存符号，如果是负数，则取绝对值，再按正数进行运算，之后再加上符号，再判断溢出。

整体思维非常容易想到，分治思想，下面是代码。

3 自己想

int reverse(int x) {// 不管正负数，全变正数bool isNegativeNumber = false;int  xAbsoluteValue = 0;if (x < 0) {isNegativeNumber = true;if (x != INT_MIN)xAbsoluteValue = -x;elsereturn 0;}else {isNegativeNumber = false;xAbsoluteValue = x;}// 判断整数多少位【动态的】int xTemporary = xAbsoluteValue;int count = 0;for (int i = 0; i < sizeof(int)*8; i++) { // 【注意】字节数*8if (xTemporary == 0) {break;}else {count++;}xTemporary /= 10;}// 反转long long xNew = 0; // 不要用long，它在32位下也是4字节xTemporary = xAbsoluteValue;for (int i = 0; i < count; i++) {xNew = xNew * 10 + xTemporary % 10;xTemporary /= 10;}// 符号回归if (isNegativeNumber) {xNew = -xNew;}// 判断溢出if (xNew < INT_MIN || xNew > INT_MAX) {return 0;}else{return xNew;}}

在这里插入图片描述
运行结果还可以，就是系统本身不稳定，有时候是4ms，这不重要，重要的是，这种做法太啰嗦了，我先尝试按照这个思路优化一下。

去掉符号转换，这部分没有也一样

注意使用long long，而不是long，32位下前者8字节，后者和int一样4个字节

判断溢出，使用一行代码搞定，取缔if else，使用三元运算符

// 判断整数多少位【动态的】int xTemporary = x;int count = 0;for (int i = 0; i < sizeof(int) * 8; i++) { // 【注意】字节数*8if (xTemporary == 0) {break;}else {count++;}xTemporary /= 10;}// 反转long long xNew = 0; xTemporary = x;for (int i = 0; i < count; i++) {xNew = xNew * 10 + xTemporary % 10;xTemporary /= 10;}return (xNew < INT_MIN || xNew > INT_MAX) ? 0 : xNew;

好了，这个程序已经优化了很多了，还有没有空间继续优化呢？

再优化，就只能在获取整数位数下手，将其直接变成反转的条件使用。

好吧……我做不下去了，看大神解法好了。

谈一谈收获

  1. 对待算法题，重点关注逻辑，对于防御性编程等细节可以不用深究
  2. 先把逻辑在纸面上搞清楚，再写代码！
  3. int、long等数据类型的大小，根据系统位数以及编译器决定，需要实际测试一下，尽量使用sizeof等通用的东西
  4. 计算位数部分，有一点动态规划的意思，很有趣。

毫无移位，按照我这么写算法题，可以凉凉了~~~~接下来，我来学习一下大神的解法吧。

4 看大神做法，直接模仿学会

4.1 大神一

long long res = 0;
while (x) {res = res * 10 + x % 10;x /= 10;
}
return (res < INT_MIN || res > INT_MAX) ? 0 : res;

这个大神与我的思路类似，只不过比我的又进一步优化，我们学习一下。

这里最重要的一点，不需要判断多少位，也不需要暂存，不用管循环次数，循环结束的条件，就是x = 0。

这也不是本质，这题的本质是数学问题。

  • 是1234变成4321的问题
  • 是1234提取出每一个数字的问题

来看看我的算法中愚蠢的点。

// 判断整数多少位【动态的】int xTemporary = x;int count = 0;for (int i = 0; i < sizeof(int) * 8; i++) { // 【注意】字节数*8if (xTemporary == 0) {break;}else {count++;}xTemporary /= 10;}// 反转long long xNew = 0; xTemporary = x;for (int i = 0; i < count; i++) {xNew = xNew * 10 + xTemporary % 10;xTemporary /= 10;}

关注一下两个循环的条件

  • 循环32次，确定位数
  • 根据位数再反转

事实上，我想的是，先确定好位数，这样就不用每次都循环32次了，但是，我在确定位数的时候，还是循环了32次……蠢到家……

虽然不是每次循环32次，但是，这种程序结构无疑是垃圾的，尽管是双重保险，但是没有必要阿，我们警惕一下！

值得警惕的结构

抛开题目本身，我们看一看这个结构

for (int i = 0; i < sizeof(int) * 8; i++) { // 【注意】字节数*8if (xTemporary == 0) {break;}else {count++;}xTemporary /= 10;
}

for循环中，嵌套一个通过if判断的跳出循环的装置，我们来改进一下

while(xTemporary){ xTemporary /= 10;count++;}

嗯，这俩功能完全一样，但是显然后者更加简洁

现在，我们是通过中介count来完成程序，那么，可以去掉中间商吗？

当然可以！

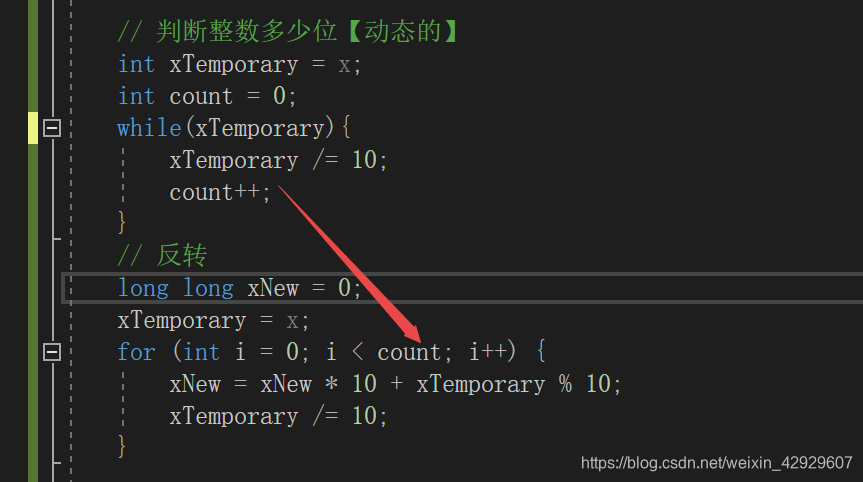
在这里插入图片描述
既然，xTemporary /= 10就可以作为终止条件，我们直接用就好了，没必要再管中间商，忽略它！

看一下我们刚才优化的本质，将x /= 10;和while(x) 二者配合，作为循环终止条件，因此，我们进一步优化。

// 判断整数多少位【动态的】int xTemporary = x;int count = 0;while(xTemporary){ xTemporary /= 10;count++;}// 反转long long xNew = 0; while(xTemporary) {xNew = xNew * 10 + xTemporary % 10;xTemporary /= 10;}

这样一来，你很容易发现，第一个循环完全没有用，直接删掉。

int reverse(int x) {long long xNew = 0; while(x) {xNew = xNew * 10 + x % 10;x /= 10;}return (xNew < INT_MIN || xNew > INT_MAX) ? 0 : xNew;
}

我们，成功将自己的烂程序一步步优化成了大神的程序。

为了程序的通用性，我们稍改一下

int reverse(int x) {long long xNew = 0; while(x != 0) {xNew = xNew * 10 + x % 10;x /= 10;}return (xNew < INT_MIN || xNew > INT_MAX) ? 0 : xNew;
}

因为只有C/C++使用0和false是一样的，但是Java就不允许，只能使用布尔值。

4.2 大神二

int reverse(int x) {int d = 0;while (x){if (d > INT_MAX / 10 || d < INT_MIN / 10)return 0;d = d * 10 + x % 10;x = x / 10;}return d;
}

我们分析大神的思路，我先缓缓下跪了！

在后面五毒神掌第二掌会分析。

5 收获

5.1 一个重要结构的优化

for循环内，通过if跳出的时候，可以优化。

for(int i = 0;i < sizeof(int)*8;i++){if(x){break;	}x /= 10
}

while(x){x /= 10
}

5.2 去掉“中间商”的方法

对于一些共性的东西，不再单独列出中间结果，直接得到最终答案。

5.3 算法的本质是数学问题

这个数学表达式其实是这么来的

  • 先分治，拆解为数字+权重的形式，本质是硬件思维
  • 再调换数字的权重
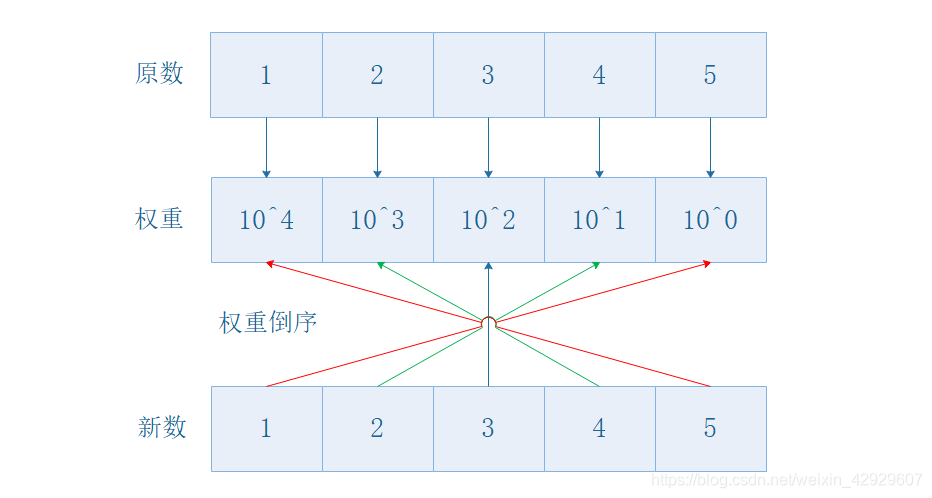
    在这里插入图片描述

至于最终的表达式，需要一点点优化过来。

我们需要知道，对于int x;

  • 求最低位的数字：x % 10
  • 降维，降低数量级：x / 10（利用int直接抹掉小数点）

第一次的算法(使用伪代码)

while(遍历每一位的数字){number[i] = x % 10;x /= 10;
}

这是很容易想到的，那么，我们保存了每一位数字，怎么保存它的权重？真的有必要保存权重吗？
显然没有必要，我们试一下就知道，可以直接一边处理旧数字，一边计算新数字。

newX = 0;
while(遍历每一位的数字){number[i] = x % 10;x /= 10;newX = newX*10 + number[i];
}

这已经是最小单元，没法解释，自己试一下吧。

然后你会发现number[i]是多余的，并且遍历的条件就是x ！= 0。

long long newX = 0;
while(x != 0){newX = newX*10 + x % 10;x /= 10;
}

至于为什么用long long，这叫先假想结果，因为结果会溢出，所以只能用long long了。

5.4 一些衍生的题目

5.4.1 求整数位数

所有整数均可。

int reverse(int x) {int count = 0;while (x){x /= 10;count++;}return count;
}

5.4.2 求整数的每一位

void reverse(int x) {int count = 0;int xTemporary = x;while (xTemporary){xTemporary /= 10;count++;}int *everyNumber = new int[count];for (int i = 0; i < count; i++) {everyNumber[i] = x % 10;x /= 10;}for (int i = 0; i < count; i++) {cout << everyNumber[i] << endl;}
}

注意

char与int转换，记得差一个'0'

int i = 4;
char a = i + '0';
cout << a << endl;

6 五毒神掌

五毒神掌是什么？

关注代码逻辑和结构层面的细节

目标导向，一天一个，完全搞定300题

6.1 第一掌

  1. 先正确理解题目
  2. 自己想，5分钟想出来就写
  3. 想不出来，就直接看世界大神答案，并且理解
  4. 然后大致理解背下来（理解代替记忆，如果不理解，就先记忆，多用用就理解了）
  5. 边抄边背的方式写代码

自己的思路不能只有一种，每种都要尝试。

重点关注逻辑！画图+手算分析

6.1.1 自己思考的过程

题目很简单，就是整数反转，需要注意

  • 正负数问题
  • 反转后溢出问题：用long long存储

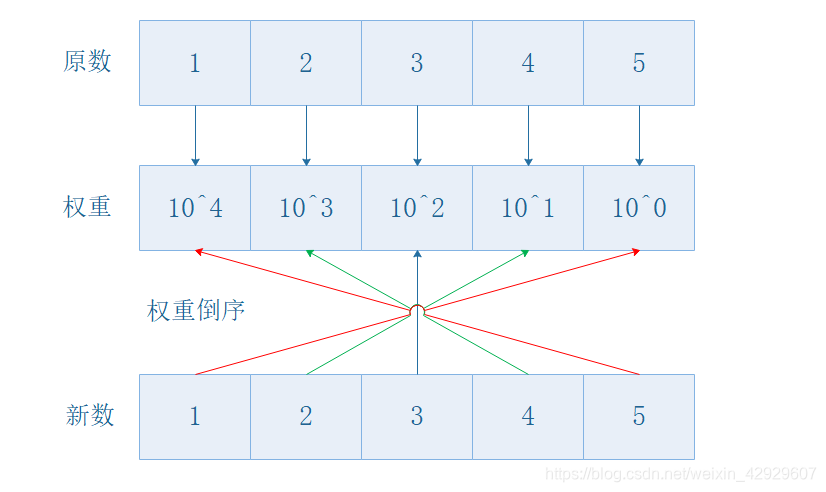
在这里插入图片描述
之后用几个数字试一试，研究一下数学公式，先写正确，再不断优化。

int reverse(int x) {long long xNew = 0;while (x != 0) {xNew = xNew * 10 + x % 10;x /= 10;}return (xNew < INT_MIN || xNew > INT_MAX) ? 0 : xNew;
}

6.1.2 大神的代码

public int reverse(int x)
{int result = 0;while (x != 0){int tail = x % 10;int newResult = result * 10 + tail;if ((newResult - tail) / 10 != result){ return 0; }result = newResult;x = x / 10;}return result;
}

基于我的思路，如果可能溢出，就直接使用更大的容器取存储数据，然后看看有没有超过小容器的值，那么，如果没有更大的容器，又该怎么办？

没有大容器，那就用2个小容器，比较新值和旧值。

对于重点公式x1新 = x1旧 * 10 + x % 10，我们知道，在数学公式中，进行等价变形，等式应该相等，也就是等式(x1新 - x%10) / 10 = x1旧成立。

但是对于计算机不同，如果第一个公式计算过程有溢出，就会丢失数据，那么第二个公式就不成立。

这也就是我们判断的重点：If overflow exists, the new result will not equal previous one.

如果溢出存在，那么，使用新值运算反过来得到的旧值，就不是原来的那个旧值。

代码如下：

int reverse(int x) {int xNew1 = 0;  // 旧值int xNew2 = 0;	// 新值while (x) {xNew2 = xNew1 * 10 + x % 10;if ((xNew2 - x % 10) / 10 != xNew1)return 0;xNew1 = xNew2;x /= 10;}return xNew2;
}

事实上，在Leetcode编译器，上面的写法是错误的！

新的收获：使用经典的测试用例

不得不说……任何的算法，在使用大量测试用例测试之前，都不一定完美，例如上面的算法，如果使用INT_MAX作为测试用例，对于能够进行溢出检测的严格编译器来说，会出现报错（不过C++编译器一般不检测……），那么，报错的原因是什么？

我们看一下xNew2 = xNew1 * 10 + x % 10;，试想一下，我们刚才假定这个过程中，编译器是允许溢出后直接截断，但不会报错，那么现在，我们假定，编译器不允许溢出的发生，我们又该怎么办？

【思维修炼】“治未病”思想：在问题发生之前处理掉

对于xNew2 = xNew1 * 10 + x % 10;，我们需要在溢出发生前，就检测出来，因此有以下程序

int reverse(int x) {int xNew = 0;while(x != 0){if(xNew > INT_MAX/10 || xNew < INT_MIN/10)	return 0;xNew = xNew * 10 + x % 10;x /= 10;}return xNew;}

更严格来说，是不是需要把x % 10也“治未病”呢？显然不需要，因为不存在一个数字，乘10后没有溢出，但是再+1就溢出了。

思考：为什么不是>=？

因为，对于极限数字214748364（也就是INT_MAX / 10），乘10之后，再加上x % 10是不可能溢出的（可以想象，如果溢出，那x % 10的结果需要 >7，那么，在这个数反转之前，就已经溢出了，所以不可能）。

经典测试案例 + 严格编译器 = 优秀算法

对于经典测试案例，例如本题，可以有

123
-123
INT_MAX
INT_MIN
1230000

这些提交前的测试案例，足够描述各种情况了。

6.1.3 小结

  1. 1个大容器与2个小容器
  2. 算法与数学公式

6.2 第二掌

把大神的代码完全不看的情况下写出来。

  • 搞定

自己的代码，多种写法，不断优化到极致。

6.3 第三掌

过了24 小时的时间以后，再次重复做题

不同解法的熟练程度 ——> 专项练习

  • 新的收获

6.3.1 整数反转图解——安检排队模型

在这里插入图片描述
如果你从动态的角度去看一下，是不是像一个U型排队区人员流动的样子？

想一想你过安检排队的情形。
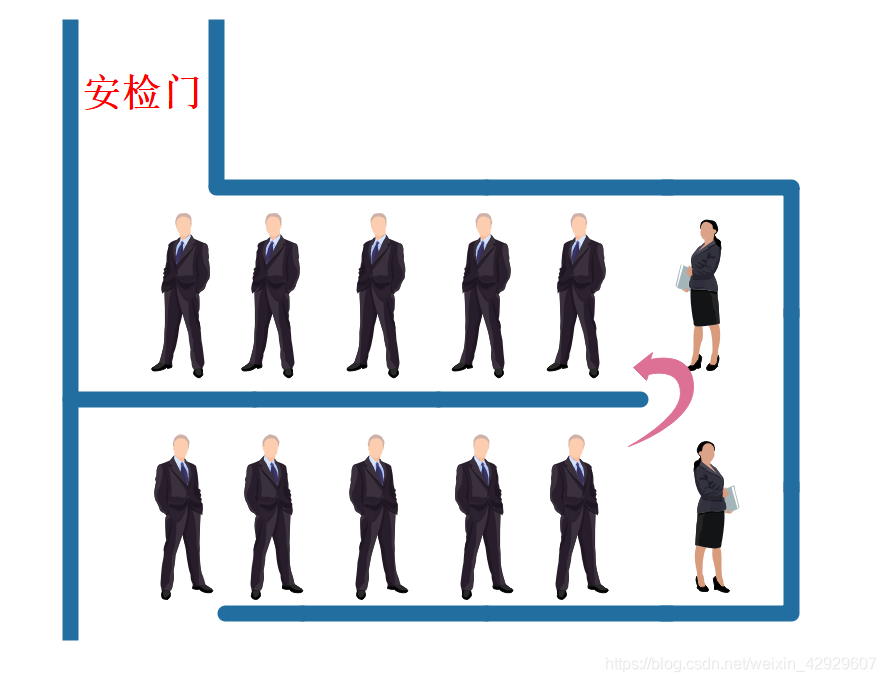
在这里插入图片描述
怎么样，是不是瞬间记住了这个整数反转模型？

int reverse(int x) {int xNew = 0;while(x){if(xNew > INT_MAX/10 || xNew < INT_MIN/10)	return 0; // 预测xNew = xNew*10 + x%10;x /= 10;}return xNew;}

通过预测提高性能

这是伟大计算机思想之一，应用广泛，例如指令操作的分支预测，在本题中，溢出的检测就使用了预测思想。

6.4 第四掌

过了一周之后: 反复回来练习相同的题目

6.5 第五掌

面试前一周恢复性的训练，所有题目全都刷一遍

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/384712.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

【蓝桥杯】BASIC-8 回文数（2020-06-08）

【蓝桥杯】BASIC-8 回文数（2020-06-08）

题目 试题 基础练习 回文数 资源限制 时间限制&#xff1a;1.0s 内存限制&#xff1a;512.0MB 问题描述 　　1221是一个非常特殊的数&#xff0c;它从左边读和从右边读是一样的&#xff0c;编程求所有这样的四位十进制数。 　　 输出格式 　　按从小到大的顺序输出满足条件的…
阅读更多...
【算法训练】Leetcode 1295. 统计位数为偶数的数字（2020.06.09 ）

【算法训练】Leetcode 1295. 统计位数为偶数的数字（2020.06.09 ）

1 题目 1295. 统计位数为偶数的数字 给你一个整数数组 nums&#xff0c;请你返回其中位数为 偶数 的数字的个数。 示例 1&#xff1a; 输入&#xff1a;nums [12,345,2,6,7896] 输出&#xff1a;2 解释&#xff1a; 12 是 2 位数字&#xff08;位数为偶数&#xff09; 345 …
阅读更多...
Vivado设置指定源文件进行RTL优化

Vivado设置指定源文件进行RTL优化

像VS编译器设置启动项一样&#xff0c;Vivado中&#xff0c;也有类似设计&#xff0c;可以看到&#xff0c;当前选中的是ALU&#xff0c;那么进行RTL优化的时候&#xff0c;会优化RTL的结果&#xff0c;而不是别的&#xff0c;如何改成别的&#xff1f; 在某文件上右键单击选择…
阅读更多...
【完整流程】用VSCode替换Vivado默认编辑器

【完整流程】用VSCode替换Vivado默认编辑器

本文楼主找了很多资料&#xff0c;选出了最有用的资料&#xff0c;按照教程走&#xff0c;就可以顺利搞定&#xff0c;先给出画面 很酷很方便&#xff0c;同时还有 自动补全检测错误列选自动生成仿真测试文件 等重要功能 Vivado原来的编辑器是这样的…… 关键是&#xff0c…
阅读更多...
IEDA中JavaDoc的自动生成、手动生成，以及生成html文档

IEDA中JavaDoc的自动生成、手动生成，以及生成html文档

1 自动生成类的注释 JavaDoc就是java特有的一种注释。 1.1 配置 首先&#xff0c;IDEA点击File-->Settings 然后Editor-->File and Code Templates-->Class 之后在这地方&#xff0c;添加一些代码 /** * ${description} * * <p> * 创建日期&#xff1a;$…
阅读更多...
【java】父类与子类的引用赋值关系

【java】父类与子类的引用赋值关系

理清楚4个目标 父类引用&#xff08;“名”&#xff09;父类对象&#xff08;“实”&#xff09;子类引用子类对象 理清楚几个操作 // 父类 public class parent{}// 子类 public class sun{}父类引用指向父类对象 parent p1 new parent();子类引用指向子类对象 son s1 …
阅读更多...
IDEA自动生成 构造方法 get set方法

IDEA自动生成 构造方法 get set方法

对于一个类&#xff0c;创建好成员变量后 右键单击&#xff0c;选中Generate 然后 这几个依次是 构造方法getsetget和set 我们可以选中一个&#xff0c;然后选中要生成的变量&#xff0c;点击OK 这样就可以自动生成 构成方法get方法set方法
阅读更多...
IDEA快速修改类名和文件名

IDEA快速修改类名和文件名

在你要修改的类名上&#xff0c;选中类名&#xff0c;然后 右键单击选中Refactor选中Rename 也可以使用快捷键 Win用户是Shift F6
阅读更多...
【FPGA VerilogHDL】第一次尝试：LED灯基础实验

【FPGA VerilogHDL】第一次尝试：LED灯基础实验

0 实验环境 0.1 软件环境 ISE 14.7win10vivado 2017.4 0.2 硬件设备 ISE适用的FPGA开发板&#xff1a;ALINK AX309 1 需求 能够灵活控制4个LED灯 2 Verilog实现 timescale 1ns / 1ps // // Create Date: 14:18:20 08/08/2020 // Module Name: led // Revision…
阅读更多...
使用ISE一键生成bit文件

使用ISE一键生成bit文件

我们知道&#xff0c;这几个&#xff0c;在第一次做好源文件之后&#xff0c;需要一个个进行右键单击-->run&#xff0c;以发现错误。 但是之后的调试&#xff0c;只要一点点变化&#xff0c;哪怕是注释变化&#xff0c;都需要重新run3次&#xff0c;太麻烦了。 不过经过实…
阅读更多...
【FPGA Verilog】实验二：key按键基础实验

【FPGA Verilog】实验二：key按键基础实验

只说一下经验和教训 1 必须按照设计流程走 不要因为实验简单&#xff0c;就直接进行综合&#xff0c;比如按照 设计编码RTL优化仿真综合管脚分配&#xff0c;实现下载 一定要按照这个步骤来。 2 必须先查看开发板说明文档 开始出了一个令人困惑的问题&#xff0c;后来发现…
阅读更多...
【Java】字符串转换为数字：Integer的parseInt方法

【Java】字符串转换为数字：Integer的parseInt方法

Java官方文档[1]的解释 public static int parseInt​(String s) throws NumberFormatException Parses the string argument as a signed decimal integer. The characters in the string must all be decimal digits, except that the first character may be an ASCII minus…
阅读更多...
在win10上使用Vmware安装Mac OS

在win10上使用Vmware安装Mac OS

安装macOS 如何在Windows上VMware上安装macOS Catalina 10.15 做一些提示&#xff1a; 如果您在第一次启动mac的时候&#xff0c;在出现【语言选择】之前&#xff0c;出现了连接蓝牙内容。 您可以将教程中【修改为win10 x64】那一步跳过&#xff0c;请注意&#xff0c;如果您…
阅读更多...
【Computer Organization】The Core Design Thinking of single cycle CPU

【Computer Organization】The Core Design Thinking of single cycle CPU

1 Overview This section introduces someting that maybe you need to know before learning. Note:This CPU is based on MIPS instruction set. 1.1 Tools LogisimCS 3410 ComponentsMARS MIPS simulatorWin10 or Mac OS 1.2 Courses 自己动手画CPU《计算机组织与结构实…
阅读更多...
【汇编语言】王爽 - 内中断复习

【汇编语言】王爽 - 内中断复习

0 前言 基于王爽《汇编语言》和Coursera的《计算机组成》课程。 1 中断分类 CPU在执行指令的过程中&#xff0c;产生了一个异常/中断&#xff0c;因为CPU只能同时执行一条指令&#xff0c;所以需要暂停该指令的执行&#xff0c;转而去处理异常/中断信息。 这个异常可以来…
阅读更多...
【算法】蛮力法/穷举法/枚举法 的基本问题分析

【算法】蛮力法/穷举法/枚举法 的基本问题分析

炮兵问题的优化&#xff0c;设立逻辑数组 蛮力法设计思想 有策略地穷举 验证 制定穷举策略避免重复 简单来说&#xff0c;就是列举问题所有可能的解&#xff0c;然后去看看是否满足题目要求&#xff0c;是一种逆向解题方式。&#xff08;我也不知道答案是什么&#xff0c;…
阅读更多...
【计算机网络实验·北航】实验一：网络实验入门（１）

【计算机网络实验·北航】实验一：网络实验入门（１）

1.3 远程在线环境使用 PCA、PCB、PCC和PCD&#xff1a;4台PC机S1、S2&#xff1a;2台交换机R1、R2&#xff1a;2台路由器中间的设备&#xff1a;组网连线器 远程组网连线&#xff1a;　使用PCA上的组网连线软件&#xff0c;配置组网连线器&#xff0c;实现组网连线。 PCA和PCB…
阅读更多...
【操作系统】虚拟化CPU、Memory，共享文件

【操作系统】虚拟化CPU、Memory，共享文件

几个概念 CPU、虚拟CPU进程内存、虚拟地址空间 物理的CPU被OS虚拟成了多个虚拟的CPU&#xff0c;这些虚拟CPU分别运行各自的程序&#xff0c;这些正在运行的程序被称为进程。物理内存被OS虚拟成了多个虚拟地址空间&#xff0c;每个进程都有独立的、自己的地址空间&#xff0c;…
阅读更多...
【Linux】编译C语言文件（-o -lpthread）

【Linux】编译C语言文件（-o -lpthread）

在gcc中使用-o编译 对于一个一般的程序&#xff0c;直接使用gcc <C语言文件名> -o <编译后生成的文件名>即可&#xff0c;例如以下程序&#xff1a; // cpu.c #include <stdio.h> #include <unistd.h> #include <stdlib.h>int main(int argc,…
阅读更多...
【Linux】Ubuntu下进行C语言编程

【Linux】Ubuntu下进行C语言编程

前言 需要您会使用Windows下cd切换目录的基本命令&#xff0c;否则请先自学相关知识&#xff0c;之后再阅读本文。 0 基础命令 介绍最基础的Linux终端命令。 su - root&#xff1a;切换到root用户&#xff08;不用也可以&#xff09;ls&#xff1a;查看当前目录位置cd&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023