使用python学线性代数

A neural network is a powerful tool often utilized in Machine Learning because neural networks are fundamentally very mathematical. We will use our basics of Linear Algebra and NumPy to understand the foundation of Machine Learning using Neural Networks. Our article is a showcase of the application of Linear Algebra and, Python provides a wide set of libraries that help to build our motivation of using Python for machine learning.

神经网络是机器学习中经常使用的强大工具，因为神经网络从根本上说是非常数学的。 我们将使用线性代数和NumPy的基础知识来理解使用神经网络进行机器学习的基础。 我们的文章展示了线性代数的应用，Python提供了广泛的库，有助于建立我们使用Python进行机器学习的动机。

The figure is showing the simplest neural network of two input nodes and one output node.

该图显示了具有两个输入节点和一个输出节点的最简单的神经网络。

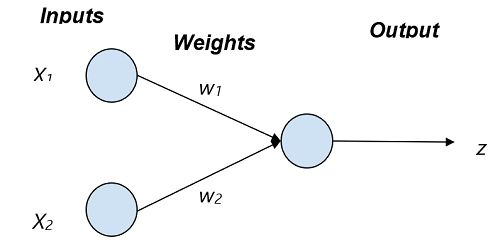
Simplest Neural Network: 2 Input - 1 Output Node

最简单的神经网络：2输入-1输出节点

Input to the neural network is X₁ and X₂ and their corresponding weights are w₁ and w₂ respectively. The output z is a tangent hyperbolic function for decision making which have input as sum of products of Input and Weight. Mathematically,

输入到神经网络的是X ₁和X ₂ ，它们相应的权重分别是w ₁和w ₂ 。 输出z是用于决策的正切双曲函数，其输入为输入与权重的乘积之和。 数学上

    z = tanh(X1w1 + X2w2)

Where, tanh() is an tangent hyperbolic function because it is one of the most used decision making functions.

其中， tanh()是切线双曲函数，因为它是最常用的决策函数之一。

So for drawing this mathematical network in a python code by defining a function neural_network( X, W). Note: The tangent hyperbolic function takes input within range of 0 to 1.

因此，通过定义函数Neuro_network(X，W)以python代码绘制此数学网络。 注意：正切双曲函数的输入范围为0到1。

Parameter(s):

参数：

    Vector X  = [[X1][X2]] and W = [[w1][w2]]

Return value:

返回值：

A value ranging between 0 and 1, as a prediction of the neural network based on the inputs.

一个介于0到1之间的值，作为基于输入的神经网络的预测。

Application:

应用：

1. Machine Learning

   机器学习

2. Computer Vision

   计算机视觉

3. Data Analysis

   数据分析

4. Fintech

   金融科技

# Linear Algebra and Neural Network
# Linear Algebra Learning Sequence
# Simplest Neural Network for 2 input 1 output node
import numpy as np
# Use of np.array() to define an Input Vector
V = np.array([.323,.432])
print("The Vector A : ",V)
# defining Weight Vector
VV = np.array([.3,.63,])
print("\nThe Vector B : ",VV)
# defining a neural network for predicting an 
# output value
def neural_network(inputs, weights):
wT = np.transpose(weights)
elpro = wT.dot(inputs)
# Tangent Hyperbolic Function for Decision Making
out = np.tanh(elpro)
return out
outputi = neural_network(V,VV)
# printing the expected output
print("Expected Output of the given Input data and their respective Weight : ", outputi)

Output:

输出：

The Vector A :  [0.323 0.432]
The Vector B :  [0.3  0.63]
Expected Output of the given Input data and their respective Weight :  0.35316923056117167

翻译自: https://www.includehelp.com/python/introduction-to-simplest-neural-network.aspx

使用python学线性代数