给你一个整数数组 nums 和两个整数 k 和 t。请你判断是否存在 两个不同下标i和j，使得 abs(nums[i] - nums[j]) <= t，同时又满足 abs(i - j) <= k。

如果存在则返回 true，不存在返回 false。

示例 1：
输入：nums = [1,2,3,1], k = 3, t = 0
输出：true

示例 2：
输入：nums = [1,0,1,1], k = 1, t = 2
输出：true

示例 3：
输入：nums = [1,5,9,1,5,9], k = 2, t = 3
输出：false

提示：
$0<=nums.length<=2\ast 10^4$
$-2^{31}<=nums[i]<=2^{31}-1$
$0<=k<=10^4$
$0<=t<=2^{31}-1$

思路：由于对于一个数 $x$，只要找到存在$[x-t,x+t]$内的数就算成功，于是采用桶的思想，桶的大小设为 $t+1$，此时桶内的极差为 $t$，即桶内的任意的两个数的差都符合条件，因此若某个桶同时出现两个及以上的元素即说明 $true$，而对于数 $x$ 既可向前找 $t$ 个数，也可向后找 $t$ 个数，因此还需观察相邻桶中的元素，相邻桶若存在与该数的差值不大于 $t$ 则 $true$，而由于某桶中出现两个元素就直接成功了，因此相邻桶要么没有元素，要么只有一个元素（因此采用哈希表实现桶），因此只需比对常数级次数。而对于限制条件 $k$，只需模拟大小 $k+1$ 的滑动窗口，从左到右遍历数组，每次从右端加入新的数并且删除最左端的数

官方题解：

class Solution {
public:int getID(int x, long w) {return x < 0 ? (x + 1ll) / w - 1 : x / w;}bool containsNearbyAlmostDuplicate(vector<int>& nums, int k, int t) {unordered_map<int, int> mp;int n = nums.size();for (int i = 0; i < n; i++) {long x = nums[i];int id = getID(x, t + 1ll);if (mp.count(id)) {return true;}if (mp.count(id - 1) && abs(x - mp[id - 1]) <= t) {return true;}if (mp.count(id + 1) && abs(x - mp[id + 1]) <= t) {return true;}mp[id] = x;if (i >= k) {mp.erase(getID(nums[i - k], t + 1ll));}}return false;}
};作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/contains-duplicate-iii/solution/cun-zai-zhong-fu-yuan-su-iii-by-leetcode-bbkt/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

代码解释：

哈希映射函数

int getID(int x, long w) {return x < 0 ? (x + 1ll) / w - 1 : x / w;
}

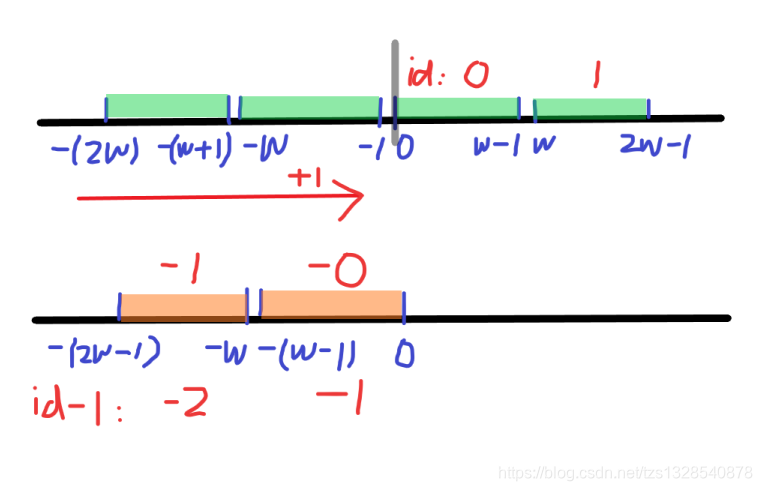
正数部分很好理解，主要讨论负数部分

1. 首先将负数都加1，由图可以看到加1后负数的坐标恰好与右边正数形成镜像映射，于是对称的两边的 $id$ 互为相反数
2. 为解决 $+0$ 与 $-0$ 的 $id$ 冲突，于是将负数桶的 $id$ 均减1