算法---递归

递归结题三部曲

何为递归？程序反复调用自身即是递归。

我自己在刚开始解决递归问题的时候，总是会去纠结这一层函数做了什么，它调用自身后的下一层函数又做了什么…然后就会觉得实现一个递归解法十分复杂，根本就无从下手。

相信很多初学者和我一样，这是一个思维误区，一定要走出来。既然递归是一个反复调用自身的过程，这就说明它每一级的功能都是一样的，因此我们只需要关注一级递归的解决过程即可。
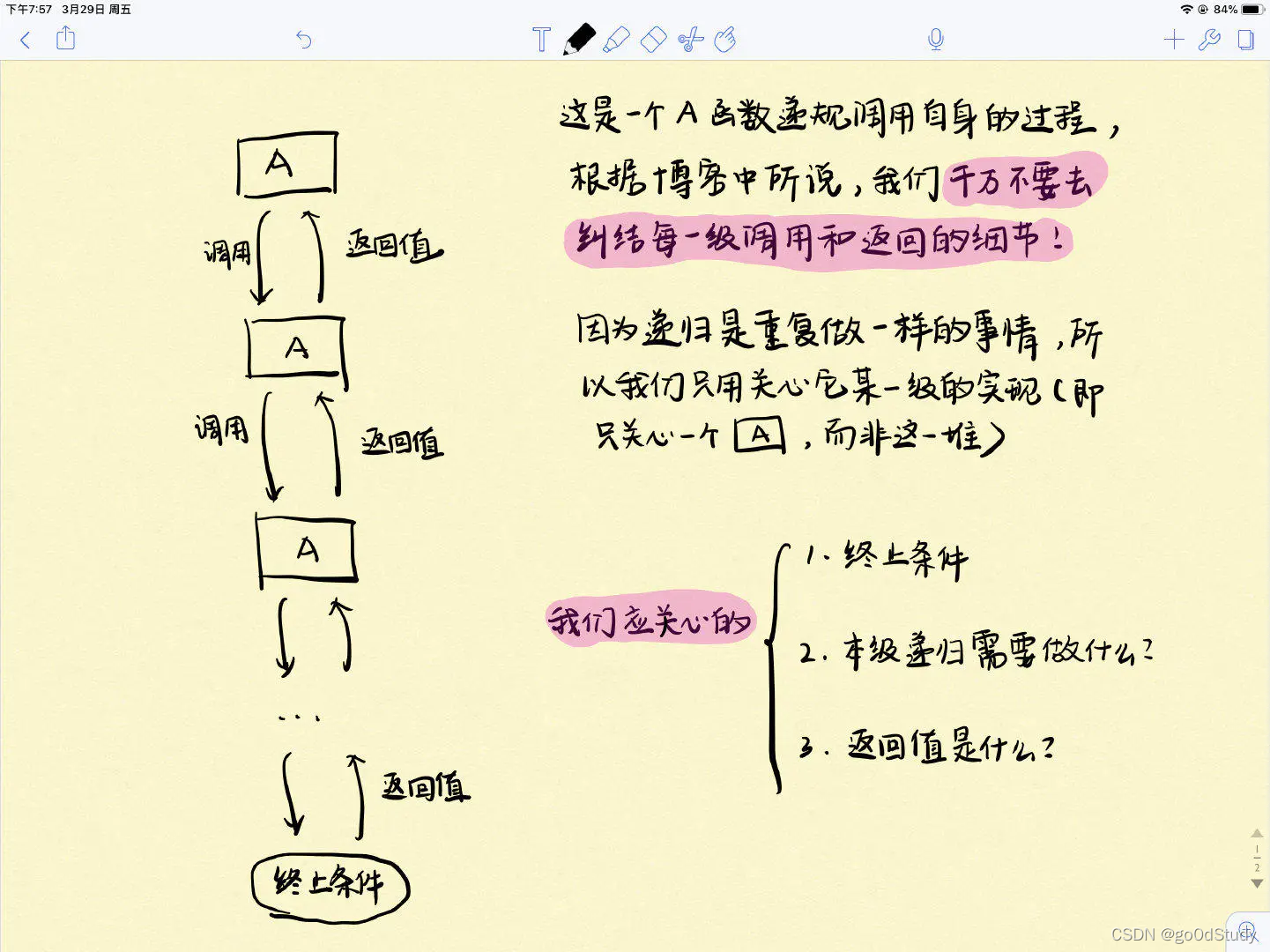
在这里插入图片描述
从图中可以看出，递归是先递后归，自下往上处理。

如上图所示，我们需要关心的主要是以下三点：

整个递归的终止条件。
一级递归需要做什么？
应该返回给上一级的返回值是什么？

因此，也就有了我们解树形递归的三部曲：

找到整个递归的终止条件：递归应该在什么时候结束？
找返回值：本级应该给上一级返回什么信息？
本级递归应该做什么：在这一级递归中，应该完成什么任务？

定要理解这3步，这就是以后递归秒杀算法题的依据和思路。

但这么说好像很空，我们来以题目作为例子，看看怎么套这个模版，相信5道题下来，你就能慢慢理解这个模版。之后再解这种套路递归题都能直接秒了

例1：求二叉树的最大深度

先看一道简单的LEEDCode题目：104. 二叉树的最大深度

直接套递归结题三部曲：

找终止条件：什么情况下不在递归下去？当然是树为空的时候，此时树的深度为0，递归就结束了。
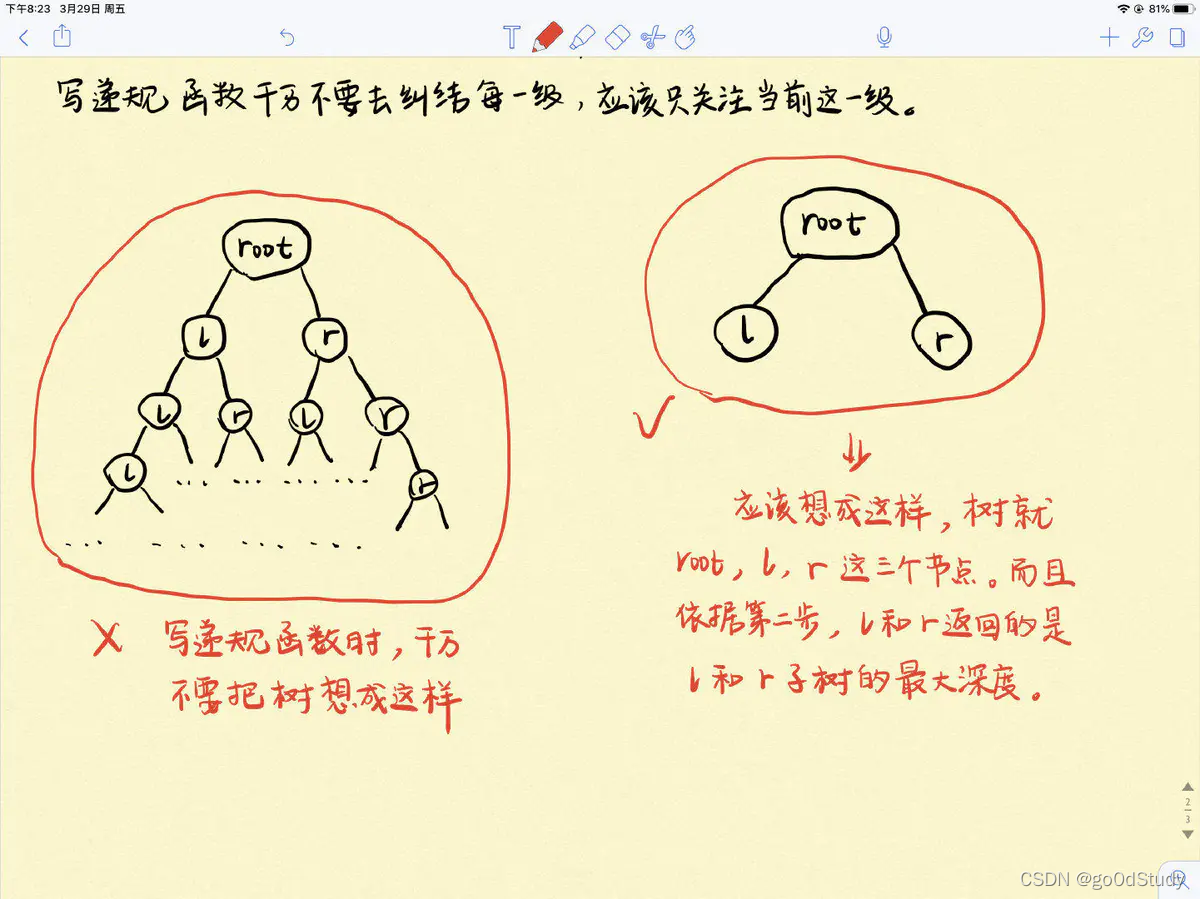
找返回值：本级应该返回给上一级什么信息？题目是要我们求最大深度，我们需要返回的当然是当前级对应的树的最大深度，比如下图的右边，返回值应该是root的最大深度，root的下一级有l和r
本级应该做什么：首先，还是强调要走出之前的思维误区，递归后我们眼里的树一定是下图右边。此时就三个节点：root、root.left、root.right，根据第二步，root.left和root.right分别记录的是root的左右子树的最大深度，那么本级递归应该做的就很明确了，那就是在root的左右子树中选择一个较大的一个，加上1就是root的最大深度了，然后再返回这个深度即可

int maxDepth(struct TreeNode* root){if(root==NULL){return 0;}/* root的左右子树最大高度 */int leftDepth = maxDepth(root->left);int rightDepth = maxDepth(root->right);/* 返回值是左右子树最大深度加1 */return leftDepth>rightDepth?(leftDepth+1):(rightDepth+1);
}

例2 ：两两交换链表中的结点。

看了一道递归套路解决二叉树的问题后，有点套路搞定递归的感觉了吗？我们再来看一道Leetcode中等难度的链表的问题，掌握套路后这种中等难度的问题真的就是秒：Leetcode 24. 两两交换链表中的节点

三部曲模板：

找终止条件：什么情况下终止？没有办法交换的时候，递归就停止。因此当链表只剩一个结点或者没有几点的时候，自然递归就终止了。
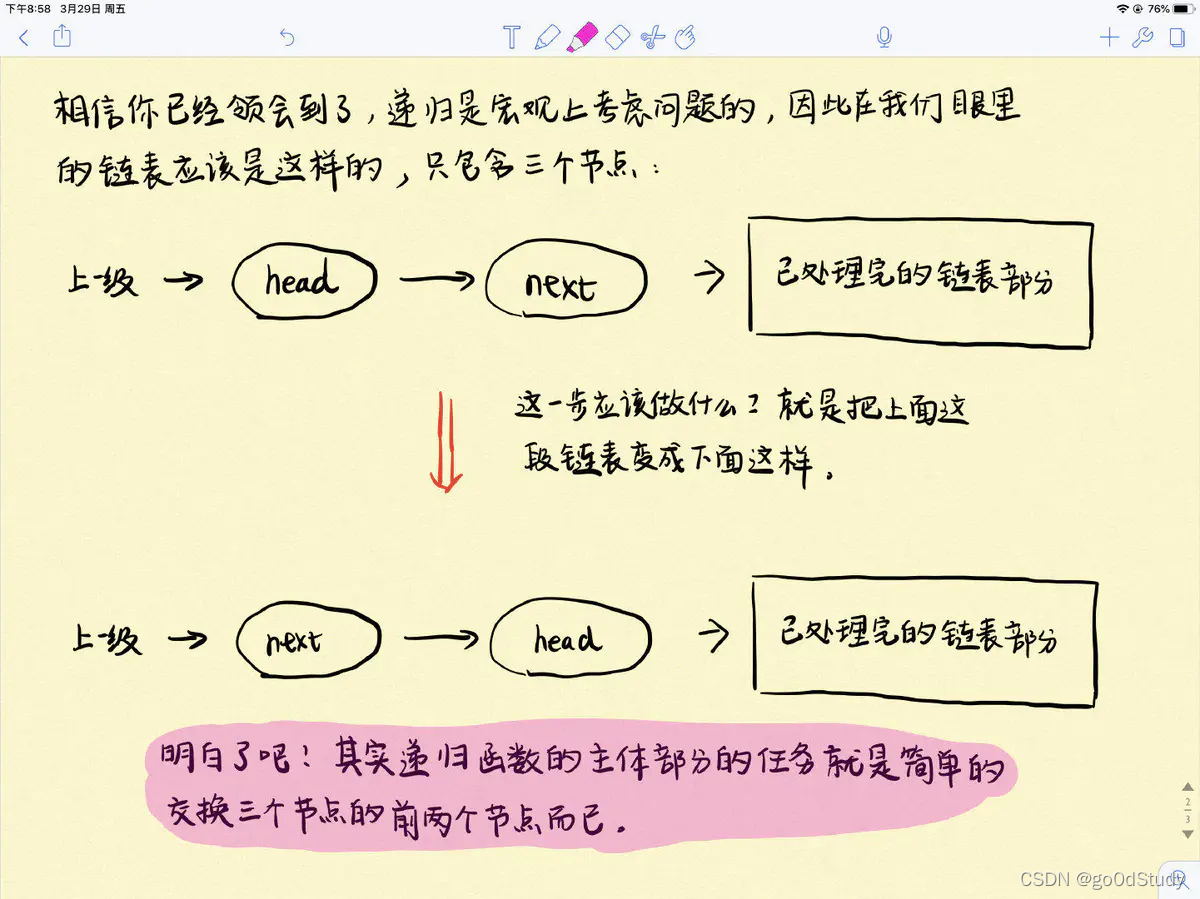
找返回值：本级希望向上一级返回的信息是什么？由于我们的目的是两两交换链表中相邻的结点，因此自然希望交换给上一级递归的是本级已经处理好的链表。
本级应该做什么？题目让交换相邻两个节点，所以我们应该交换相邻两个节点，涉及三个结点，两个指针，head结点，head->next结点，以及head->next->next后面已经处理好的链表，我们看做一个结点。本级递归的任务就是交换这3个结点中的前两个结点。

在这里插入图片描述

struct ListNode* swapPairs(struct ListNode* head) {/* 终止条件 */if (head == NULL || head->next == NULL) {return head;}/* 获取head->next结点 */struct ListNode*next = head->next;/* swapPairs(next->next)代表已经处理好的链表，交换两个节点，我们要让head指向这个结点 */head->next = swapPairs(next->next);/* next指向head结点 此时next就是该链表的头结点*/next->next = head;/* 返回本级处理好的链表 */return next;
}

例3：平衡二叉树

相信经过以上2道题，你已经大概理解了这个模版的解题流程了。

那么请你先不看以下部分，尝试解决一下这道easy难度的Leetcode题（个人觉得此题比上面的medium难度要难）：Leetcode 110. 平衡二叉树

我觉得这个题真的是集合了模版的精髓所在，下面套三部曲模版：

终止条件：什么情况下终止？自然是子树为空的时候，空树是平衡二叉树。
返回值：为什么我说这个题是集合了模版精髓？正是因为此题的返回值。要知道我们搞这么多花里胡哨的，都是为了能写出正确的递归函数，因此在解这个题的时候，我们就需要思考，我们到底希望返回什么值？何为平衡二叉树？平衡二叉树即左右两棵子树高度差不大于1的二叉树。而对于一颗树，它是一个平衡二叉树需要满足三个条件：它的左子树是平衡二叉树，它的右子树是平衡二叉树，它的左右子树的高度差不大于1。换句话说：如果它的左子树或右子树不是平衡二叉树，或者它的左右子树高度差大于1，那么它就不是平衡二叉树。两个条件才能判断是不是平衡二叉树。
而在我们眼里，这颗二叉树就3个节点：root、left、right。那么我们应该返回什么呢？如果返回一个当前树是否是平衡二叉树的boolean类型的值，那么我只知道left和right这两棵树是否是平衡二叉树，无法得出left和right的高度差是否不大于1，自然也就无法得出root这棵树是否是平衡二叉树了。而如果我返回的是一个平衡二叉树的高度的int类型的值，那么我就只知道两棵树的高度，但无法知道这两棵树是不是平衡二叉树，自然也就没法判断root这棵树是不是平衡二叉树了。
因此，我们定义一个结构体，该结构体包含结点的深度，以及该节点是不是平衡二叉树。

struct inf{int length;//当前节点的长度bool isB;  //当前节点是不是平衡树};

返回值就是当级节点的深度以及该节点是不是平衡二叉树。如果不是平衡二叉树，返回值的深度为0

本级递归该做什么？知道了第二步的返回值后，我们应该先获得当前节点左右子树的struct inf信息，即左右子树的深度以及是不是平衡二叉树。然后判断左右子树是不是平衡二叉树以及高度差是否大于1。

struct inf{int length;//当前节点的长度bool isB;  //当前节点是不是平衡树};
struct inf *tru ;   /* 表示一个节点的初始状态是平衡二叉树 */
struct inf *fal ;   /* 表示不是平衡二叉树 */struct inf *getInf(struct TreeNode *root)
{if(root==NULL){return tru; }/* 获取左右子树的深度以及是不是平衡二叉树信息 */struct inf *right = getInf(root->right);struct inf *left  = getInf(root->left);/*判断左右子树是不是平衡二叉树*/if(right->isB == false || left->isB == false ){return fal;}/* 高度差是否大于1 */if(abs(right->length-left->length)>1){return fal;}/* 返回值左右子树深度最大值加1并且是平衡二叉树 */struct inf *ret = (struct inf *)malloc(sizeof(struct inf));ret->length = fmax(left->length,right->length)+1;ret->isB = true;return ret;}bool isBalanced(struct TreeNode* root){tru = (struct inf *)malloc(sizeof(struct inf));tru->length=0;tru->isB=true;fal = (struct inf *)malloc(sizeof(struct inf));fal->length=0;fal->isB = false;struct inf *ret = getInf(root);if(ret->isB==true)return true;elsereturn false;
}