二叉排序树(Binary Sort Tree) 又称为二叉查找树(Binary Search Tree) - （代码、分析）

目录：

    • 代码：
    • 分析：

代码：

BSTree.h

#ifndef _BSTREE_H_
#define _BSTREE_H_typedef void BSTree;//定义二叉树类型
typedef void BSKey;//定义节点的键值类型（用于节点排序）typedef struct _tag_BSTreeNode BSTreeNode;//定义二叉树节点类型
struct _tag_BSTreeNode
{BSKey* key;//键值BSTreeNode* left;//左子节点BSTreeNode* right;//右子节点
};typedef void (BSTree_Printf)(BSTreeNode*);//定义参数为一个节点指针并且无返回值的函数类型
typedef int (BSTree_Compare)(BSKey*, BSKey*);//定义参数为两个键值指针并且无返回值的函数类型BSTree* BSTree_Create();//声明创建树函数void BSTree_Destroy(BSTree* tree);//声明销毁树函数void BSTree_Clear(BSTree* tree);//声明清空树函数int BSTree_Insert(BSTree* tree, BSTreeNode* node, BSTree_Compare* compare);//声明插入节点函数BSTreeNode* BSTree_Delete(BSTree* tree, BSKey* key, BSTree_Compare* compare);//声明删除节点函数BSTreeNode* BSTree_Get(BSTree* tree, BSKey* key, BSTree_Compare* compare);//声明获取节点函数BSTreeNode* BSTree_Root(BSTree* tree);//声明获取根节点函数int BSTree_Height(BSTree* tree);//声明获取树高度函数int BSTree_Count(BSTree* tree);//声明获取节点数量函数int BSTree_Degree(BSTree* tree);//声明获取树度数函数void BSTree_Display(BSTree* tree, BSTree_Printf* pFunc, int gap, char div);//定义统一用函数处理节点函数#endif

BSTree.c

#include <stdio.h>
#include <malloc.h>
#include "BSTree.h"typedef struct _tag_BSTree TBSTree;//定义实际使用二叉树类型
struct _tag_BSTree
{int count;//数量BSTreeNode* root;//根节点
};
//用递归调用函数处理节点函数
static void recursive_display(BSTreeNode* node, BSTree_Printf* pFunc, int format, int gap, char div) // O(n)
{int i = 0;if( (node != NULL) && (pFunc != NULL) ){for(i=0; i<format; i++){printf("%c", div);}pFunc(node);printf("\n");if( (node->left != NULL) || (node->right != NULL) ){recursive_display(node->left, pFunc, format + gap, gap, div);recursive_display(node->right, pFunc, format + gap, gap, div);}}else{for(i=0; i<format; i++){printf("%c", div);}printf("\n");}
}static int recursive_count(BSTreeNode* root) //递归计算节点数量函数（没使用到）
{int ret = 0;if( root != NULL ){ret = recursive_count(root->left) + 1 + recursive_count(root->right);}return ret;
}static int recursive_height(BSTreeNode* root) // 递归计算高度函数
{int ret = 0;if( root != NULL ){int lh = recursive_height(root->left);int rh = recursive_height(root->right);ret = ((lh > rh) ? lh : rh) + 1;}return ret;
}static int recursive_degree(BSTreeNode* root) //递归计算度数函数
{int ret = 0;if( root != NULL ){if( root->left != NULL ){ret++;}if( root->right != NULL ){ret++;}if( ret == 1 ){int ld = recursive_degree(root->left);int rd = recursive_degree(root->right);if( ret < ld ){ret = ld;}if( ret < rd ){ret = rd;}}}return ret;
}static int recursive_insert(BSTreeNode* root, BSTreeNode* node, BSTree_Compare* compare)
{int ret = 1;int r = compare(node->key, root->key);//1参数小于2参数返回负数，大于返回正数，等于返回0if( r == 0 )//如果两个键相等插入结果等于0返回到调用函数，表示插入失败{ret = 0;}else if( r < 0 )//如果插入节点的键小于当前比较的节点的键，表示应该是往当前比较的节点的左子节点走{if( root->left != NULL )//如果当前比较的节点的左子节点不为空{//将其左子节点作为下一个与插入节点比较的节点再调用函数进栈，是否插入成功结果返回这里ret = recursive_insert(root->left, node, compare);}else{//否则直接将插入节点作为当前比较节点的左子节点root->left = node;}}else if( r > 0 )//如果插入节点的键小于当前比较根节点的键，表示应该是往当前比较根节点的右子节点走{if( root->right != NULL )//如果当前比较的节点的右子节点不为空{//将其右子节点作为下一个与插入节点比较的节点再调用函数进栈，是否插入成功结果返回这里ret = recursive_insert(root->right, node, compare);}else{//否则直接将插入节点作为当前比较节点的右子节点root->right = node;}}return ret;//将结果返回
}static BSTreeNode* recursive_get(BSTreeNode* root, BSKey* key, BSTree_Compare* compare)//递归查找节点函数
{BSTreeNode* ret = NULL;if( root != NULL ){int r = compare(key, root->key);if( r == 0 ){ret = root;}else if( r < 0 ){ret = recursive_get(root->left, key, compare);}else if( r > 0 ){ret = recursive_get(root->right, key, compare);}}return ret;
}static BSTreeNode* delete_node(BSTreeNode** pRoot)//进行删除节点函数
{BSTreeNode* ret = *pRoot;//取得要删除节点地址if( (*pRoot)->right == NULL )//如果删除节点的右子节点等于空{*pRoot = (*pRoot)->left;//将删除节点的左子节点赋到本来指向删除节点的指针}else if( (*pRoot)->left == NULL )//如果删除节点的左子节点等于空{*pRoot = (*pRoot)->right;//将删除节点的右子节点赋到本来指向删除节点的指针}else//否则表示左右子节点都不为空{BSTreeNode* g = *pRoot;//取得要删除节点地址BSTreeNode* c = (*pRoot)->left;//取得要删除节点的左子节点地址//从删除节点左子节点开始找出一个键与删除节点键最接近的节点，作为删除节点的那个位置//因为从删除节点的左子节点开始，所以它的右子节点一直沿伸的节点的键是最接近删除节点的//c用于指向作为替换到删除节点位置的节点 g是c的父节点while( c->right != NULL )//从删除节点的左子节点往右查找，找到右节点为空的节点{g = c;//更新位置c = c->right;//更新下一个检测的位置}if( g != *pRoot )//g不等于删除节点，表示找到合适的节点{//因为c要替换到删除节点的位置，这时c节点只有左子节点（有指向或NULL）需要处理连接的，//因为c的右子节点确保为NULL了，经过上面的查找，再将c父节点的本来指向c节点的右子节点//指向c的左子节点，而且c的左子节点键肯定大于c的父节点所以是c的父节点的右子节点//相当替换了c节点原来的位置g->right = c->left;}else//否则表示删除节点的左子节点就是合适替换到删除节点位置的节点{//直接将删除节点的左子节点等于c的左子节点，这里就只有c左子节点有指向的g->left = c->left;}c->left = (*pRoot)->left;//将删除节点本来的左子节点部分赋给c节点左子节点c->right = (*pRoot)->right;//将删除节点本来的右子节部分赋给c节点的右子节点*pRoot = c;//把c节点更新到原来删除节点的指针位置}return ret;//返回删除节点
}static BSTreeNode* recursive_delete(BSTreeNode** pRoot, BSKey* key, BSTree_Compare* compare)
{BSTreeNode* ret = NULL;if( (pRoot != NULL) && (*pRoot != NULL) )//比较节点指针地址与指向不为空{  //将当前节点与key值进行比较等于0表示找到了，小于表示应该往当前节点左子节点查找，大于往右子节点查找int r = compare(key, (*pRoot)->key);if( r == 0 )//找到后调用删除节点函数进行删除{//注意：pRoot不是当前节点地址，是指向要删除节点的节点指针的地址（也就是树的根节点指针地址或是上一个节点的左子节点指针或右子节点指针地址）ret = delete_node(pRoot);//将节点指针地址作为参数进行删除操作}else if( r < 0 ){//将当前节点的左子节点指针地址调用函数继续查找ret = recursive_delete(&((*pRoot)->left), key, compare);}else if( r > 0 ){//将当前节点的右子节点指针地址调用函数继续查找ret = recursive_delete(&((*pRoot)->right), key, compare);}}return ret;
}BSTree* BSTree_Create() // 定义创建树函数
{TBSTree* ret = (TBSTree*)malloc(sizeof(TBSTree));if( ret != NULL ){ret->count = 0;ret->root = NULL;}return ret;
}void BSTree_Destroy(BSTree* tree) // 定义销毁树函数
{free(tree);
}void BSTree_Clear(BSTree* tree) // 定义清空树函数
{TBSTree* btree = (TBSTree*)tree;if( btree != NULL ){btree->count = 0;btree->root = NULL;}
}int BSTree_Insert(BSTree* tree, BSTreeNode* node, BSTree_Compare* compare) //定义插入节点函数
{TBSTree* btree = (TBSTree*)tree;//取得树int ret = (btree != NULL) && (node != NULL) && (compare != NULL);//判断参数不为空if( ret ){node->left = NULL;//将插入节点左子节点设空node->right = NULL;//将插入节点右子节点设空if( btree->root == NULL )//如果根节点等于空表示是第一个节点{btree->root = node;}else{//调用递归检测插入位置ret = recursive_insert(btree->root, node, compare);}if( ret )//如果插入成功{btree->count++;//节点数量增加}}return ret;
}BSTreeNode* BSTree_Delete(BSTree* tree, BSKey* key, BSTree_Compare* compare)//定义删除节点函数
{TBSTree* btree = (TBSTree*)tree;//取得树BSTreeNode* ret = NULL; if( (btree != NULL) && (key != NULL) && (compare != NULL) )//判断参数不为空{ret = recursive_delete(&btree->root, key, compare);if( ret != NULL ){btree->count--;}}return ret;
}BSTreeNode* BSTree_Get(BSTree* tree, BSKey* key, BSTree_Compare* compare)//定义获取节点函数
{TBSTree* btree = (TBSTree*)tree;//取得树BSTreeNode* ret = NULL; if( (btree != NULL) && (key != NULL) && (compare != NULL) )//判断参数不为空{ret = recursive_get(btree->root, key, compare);//调用递归查找 }return ret;//返回获取节点
}BSTreeNode* BSTree_Root(BSTree* tree) // 定义获取根节点函数
{TBSTree* btree = (TBSTree*)tree;BSTreeNode* ret = NULL;if( btree != NULL ){ret = btree->root;}return ret;
}int BSTree_Height(BSTree* tree) // 定义获取树高度函数
{TBSTree* btree = (TBSTree*)tree;int ret = 0;if( btree != NULL ){ret = recursive_height(btree->root);//调用递归计算高度函数}return ret;
}int BSTree_Count(BSTree* tree) // 定义获取节点数量函数
{TBSTree* btree = (TBSTree*)tree;int ret = 0;if( btree != NULL ){ret = btree->count;}return ret;
}int BSTree_Degree(BSTree* tree) // 定义获取树度数函数
{TBSTree* btree = (TBSTree*)tree;int ret = 0;if( btree != NULL ){ret = recursive_degree(btree->root);//调用递归计算度数函数}return ret;
}void BSTree_Display(BSTree* tree, BSTree_Printf* pFunc, int gap, char div) //定义用统一函数处理节点函数
{TBSTree* btree = (TBSTree*)tree;if( btree != NULL ){recursive_display(btree->root, pFunc, 0, gap, div);}
}

main.c

#include <stdio.h>
#include <stdlib.h>
#include "BSTree.h"struct Node
{BSTreeNode header;char v;
};void printf_data(BSTreeNode* node)
{if( node != NULL ){printf("%c", ((struct Node*)node)->v);}
}int compare_key(BSKey* k1, BSKey* k2)
{return (int)k1 - (int)k2;
}int main(int argc, char *argv[])
{BSTree* tree = BSTree_Create();struct Node n1 = {{(BSKey*)1, NULL, NULL}, 'A'};struct Node n2 = {{(BSKey*)2, NULL, NULL}, 'B'};struct Node n3 = {{(BSKey*)3, NULL, NULL}, 'C'};struct Node n4 = {{(BSKey*)4, NULL, NULL}, 'D'};struct Node n5 = {{(BSKey*)5, NULL, NULL}, 'E'};struct Node n6 = {{(BSKey*)6, NULL, NULL}, 'F'};BSTree_Insert(tree, (BSTreeNode*)&n4, compare_key);BSTree_Insert(tree, (BSTreeNode*)&n1, compare_key);BSTree_Insert(tree, (BSTreeNode*)&n3, compare_key);BSTree_Insert(tree, (BSTreeNode*)&n6, compare_key);BSTree_Insert(tree, (BSTreeNode*)&n2, compare_key);BSTree_Insert(tree, (BSTreeNode*)&n5, compare_key);printf("Height: %d\n", BSTree_Height(tree));printf("Degree: %d\n", BSTree_Degree(tree));printf("Count: %d\n", BSTree_Count(tree));printf("Search Key 5: %c\n", ((struct Node*)BSTree_Get(tree, (BSKey*)5, compare_key))->v);printf("Full Tree: \n");BSTree_Display(tree, printf_data, 4, '-');BSTree_Delete(tree, (BSKey*)4, compare_key);printf("After Delete Key 4: \n");printf("Height: %d\n", BSTree_Height(tree));printf("Degree: %d\n", BSTree_Degree(tree));printf("Count: %d\n", BSTree_Count(tree));printf("Full Tree: \n");BSTree_Display(tree, printf_data, 4, '-');BSTree_Clear(tree);printf("After Clear: \n");printf("Height: %d\n", BSTree_Height(tree));printf("Degree: %d\n", BSTree_Degree(tree));printf("Count: %d\n", BSTree_Count(tree));BSTree_Display(tree, printf_data, 4, '-');BSTree_Destroy(tree);getchar();return 0;
}

分析：

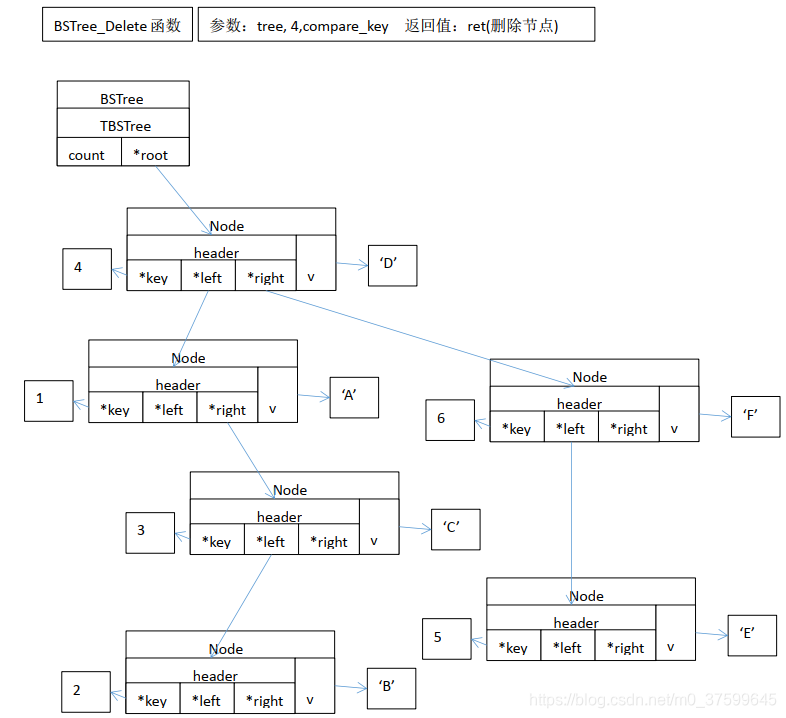
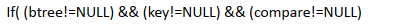
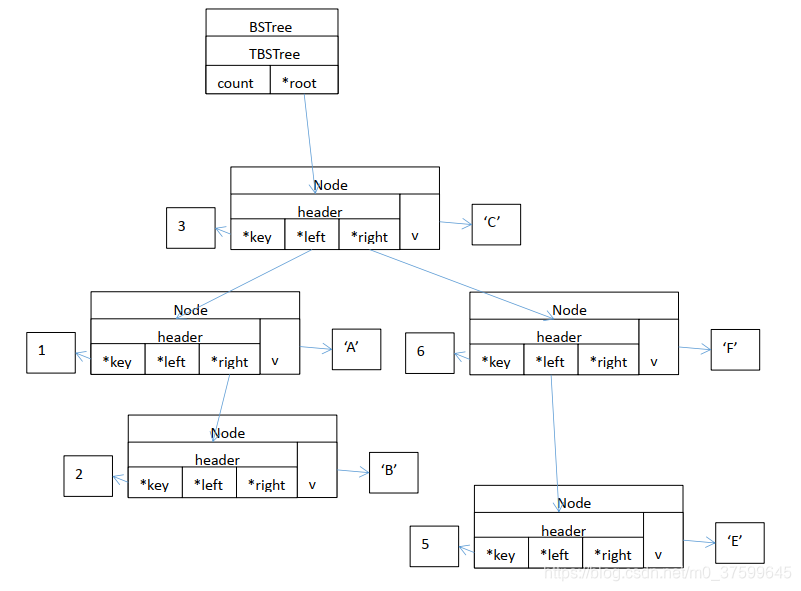
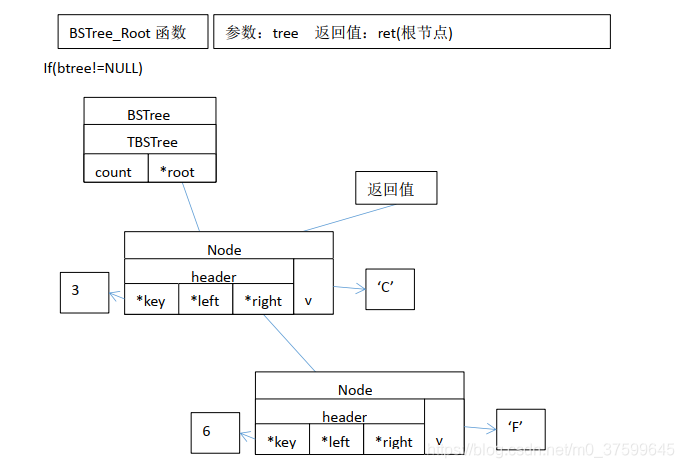
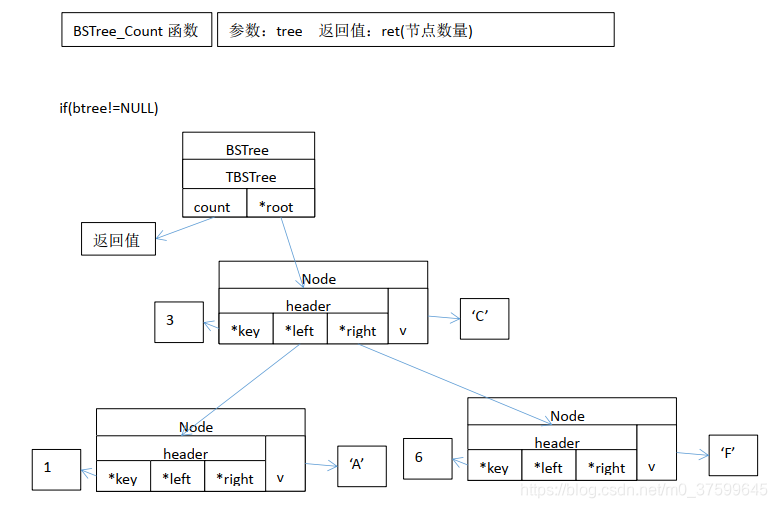
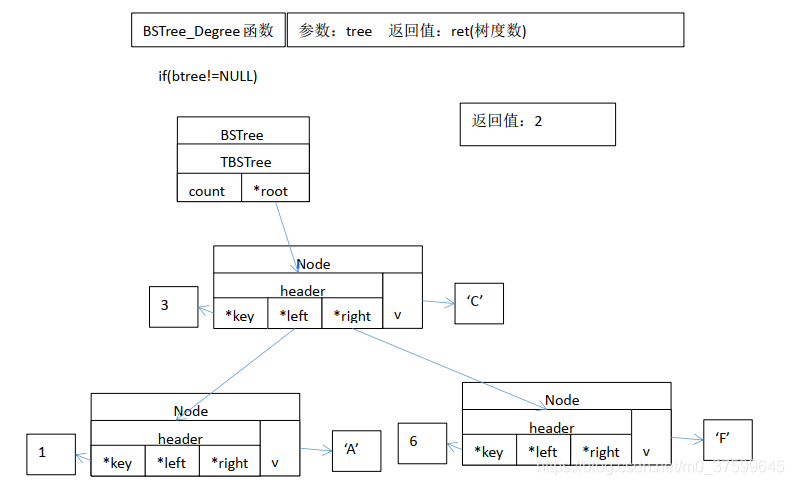
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/379133.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

springboot tomcat默认线程数_记一次JAVA线程池的错误用法

springboot tomcat默认线程数_记一次JAVA线程池的错误用法

最近项目一个项目要结项了&#xff0c;但客户要求 TPS 能达到上千&#xff0c;而用我写的代码再怎么弄成只能达到 30 的 TPS&#xff0c;然后我又将代码中能缓存的都缓存了&#xff0c;能拆分的也都拆分了&#xff0c;拆分时用的线程池来实现的&#xff1b;其实现的代码主要为…
阅读更多...
引以为鉴-ARM开发板连线注意事项

引以为鉴-ARM开发板连线注意事项

前些日子把实验室的三台机子放到一个工位上&#xff0c;非常拥挤&#xff0c;做实验也很不方便。因此&#xff0c;想把ARM开发板的环境重新搭建到自己的电脑上。说完就做&#xff0c;上午就开始忙活起来。把开发板上的USB线、串口线、JTAT接口、还有电源线一一插好。接着就开始…
阅读更多...
Python---实验八

Python---实验八

1&#xff0c;现在有一份‘邀请函.txt’的空白文件&#xff0c;请在同级目录下编写一段代码&#xff0c;写入内容‘诚挚邀请您来参加本次宴会’。 with open(fG:\study\Python\邀请函.txt,modew,encodingutf-8) as y:y.write(诚挚邀请您来参加本次宴会)效果图如下&#xff1a;…
阅读更多...
哈希表 - （代码、分析 ）

哈希表 - （代码、分析 ）

目录&#xff1a;代码&#xff1a;分析&#xff1a;代码&#xff1a; BSTree.h BSTree.c 二叉排序树(Binary Sort Tree) 又称为二叉查找树(Binary Search Tree) Hash.h #ifndef _HASH_H_ #define _HASH_H_typedef void Hash;//定义哈希表类型 typedef void HashKey;//定义哈…
阅读更多...
scala spark 数据对比_IT大牛耗时三个月总结出大数据领域学习路线，网友评论：炸锅了...

scala spark 数据对比_IT大牛耗时三个月总结出大数据领域学习路线，网友评论：炸锅了...

大数据不是某个专业或一门编程语言&#xff0c;实际上它是一系列技术的组合运用。有人通过下方的等式给出了大数据的定义。大数据 编程技巧 数据结构和算法 分析能力 数据库技能 数学 机器学习 NLP OS 密码学 并行编程虽然这个等式看起来很长&#xff0c;需要学习的东…
阅读更多...
Python---实验九作业

Python---实验九作业

1&#xff0c;使用tkinter实现计算器程序。实现效果如下&#xff1a; from tkinter import * from tkinter.ttk import *def frame(master):"""将共同的属性作为默认值, 以简化Frame创建过程"""w Frame(master)w.pack(sideTOP, expandYES, fill…
阅读更多...
用pv操作描述如下前驱图_LinkedList实现分析（二）——常用操作

用pv操作描述如下前驱图_LinkedList实现分析（二）——常用操作

上一篇文章LinkedList实现分析(一)——LinkedList初探与对象创建介绍了LinkedList中的一些重要属性和构造方法&#xff0c;下面我们将详细介绍一下LinkedList提高的常用方法的实现原理元素添加###add(E e)方法往LinkedList添加元素&#xff0c;LinkedList提供了多重方式&#x…
阅读更多...
C++多重继承与虚基类及与.NET的比较

C++多重继承与虚基类及与.NET的比较

多重继承前面我们介绍的派生类只有一个基类&#xff0c;称为单基派生或单一继承。在实际运用中&#xff0c;我们经常需要派生类同时具有多个基类&#xff0c;这种方法称为多基派生或多重继承。2.1 多重继承的声明&#xff1a;在 C 中&#xff0c;声明具有两个以上基类的派生类与…
阅读更多...
平院实训门禁系统导入

平院实训门禁系统导入

这是我的配置&#xff08;如果是Win10最好每一步都管理员身份运行&#xff09; win7 SQLServer2008 VS2012 切记&#xff1a;注意&#xff1a;当你SQLserver创建数据库和VS连接数据库的时候得用同一种方式&#xff0c;要么都用window&#xff08;主机名&#xff09;&#xff0…
阅读更多...
北京中信银行总行地址_中信银行拉萨分行举行“存款保险标识”启用和存款保险条例宣传活动...

北京中信银行总行地址_中信银行拉萨分行举行“存款保险标识”启用和存款保险条例宣传活动...

11月NOV中信银行拉萨分行举行“存款保险标识”启用和《存款保险条例》宣传活动揭牌启用仪式111月Jul根据人民银行和总行关于“存款保险标识”启用工作相关要求&#xff0c;分行行领导高度重视“存款保险标识”启用和《存款保险条例》宣传活动工作&#xff0c;按照统一工作部署、…
阅读更多...
转整型_156.Ruby烘焙大理石豆沙吐司解锁大理石花纹整型

转整型_156.Ruby烘焙大理石豆沙吐司解锁大理石花纹整型

好看又好吃的大理石豆沙面包。红豆馅均匀分布在松软细腻的面包体里&#xff0c;手撕着吃&#xff0c;一层层的甜美与温柔&#xff5e;关于吐司面包&#xff0c;我公众号里写过白吐司(基础款牛奶吐司&#xff0c;超绵鲜奶油吐司)和全麦吐司(基础款50%全麦吐司&#xff0c;经典燕…
阅读更多...
VS2010 快捷键 （空格显示 绿点， Tab 显示箭头）

VS2010 快捷键 （空格显示 绿点， Tab 显示箭头）

VS2010 有用的快捷键 &#xff1a; Ctrl r, ctrl w, 切换空格示。 转载于:https://www.cnblogs.com/fengye87626/archive/2012/11/21/2780716.html
阅读更多...
分析一下mp4格式的trak -＞ mdia -＞ minf -＞ stbl -＞ stts、stsc 这两个box信息

分析一下mp4格式的trak -＞ mdia -＞ minf -＞ stbl -＞ stts、stsc 这两个box信息

分析一下mp4格式的trak -> mdia -> minf -> stbl -> stts、stsc 这两个box信息 &#xff08;因为这两个box在音频trak和视频trak 下都有的&#xff0c;而且都有一个数组的值是比较绕的&#xff09; 目录&#xff1a;stts&#xff1a;记录时间戳的&#xff0c;每个s…
阅读更多...
Python---爬虫案例

Python---爬虫案例

例1、爬取公众号文章中的图片。 1&#xff0c;首先打开要获取公众号文章的地址 2&#xff0c;按下F12&#xff0c;再按Ctrl Shift C&#xff0c;然后鼠标移动到图片位置&#xff0c;然后观察控制台中显示图片对应的代码位置 3&#xff0c;分析该位置的代码段 代码段如下&…
阅读更多...
Python---实验九

Python---实验九

1、使用标准库urllib爬取“http://news.pdsu.edu.cn/info/1005/31269.htm”平顶山学院新闻网上的图片&#xff0c;要求:保存到F盘pic目录中&#xff0c;文件名称命名规则为“本人姓名” “_图片编号”&#xff0c;如姓名为张三的第一张图片命名为“张三_1.jpg”。 from re imp…
阅读更多...
32接上拉5v_51单片机P0口上拉电阻的选择

32接上拉5v_51单片机P0口上拉电阻的选择

作为I/O口输出的时候时&#xff0c;输出低电平为0 输出高电平为高组态(并非5V&#xff0c;相当于悬空状态&#xff0c;也就是说P0 口不能真正的输出高电平)。给所接的负载提供电流&#xff0c;因此必须接(一电阻连接到VCC)&#xff0c;由电源通过这个上拉电阻给负载提供电流。P…
阅读更多...
[转载]FPGA/CPLD重要设计思想及工程应用(时序及同步设计)

[转载]FPGA/CPLD重要设计思想及工程应用(时序及同步设计)

来源&#xff1a;http://www.eetop.cn/blog/html/11/317611-13412.html 数字电路中,时钟是整个电路最重要、最特殊的信号。 第一, 系统内大部分器件的动作都是在时钟的跳变沿上进行, 这就要求时钟信号时延差要非常小, 否则就可能造成时序逻辑状态出错. 第二, 时钟信号通常是系统…
阅读更多...
实验五 图形设计

实验五 图形设计

每复制一个方法都要绑定Paint事件 一、创建Windows窗体应用程序&#xff0c;要求如下&#xff1a;&#xff08;源代码运行界面&#xff0c;缺少任一项为0分&#xff0c;源代码只需粘贴绘制图形代码所在的方法&#xff0c;不用粘贴太多&#xff09; 例如: &#xff08;1&…
阅读更多...
ADO.NET与SQL Server数据库的交互

ADO.NET与SQL Server数据库的交互

7.3.1 使用SqlConnection对象连接数据库 例如&#xff1a;建立与SQL Server数据库的连接。 string connstring"Data Sourceservername;uidusername;pwdpassword;Initial Catalogdbname";SqlConnection connnew SqlConnection(connstring);conn.Open(); 例如&#xf…
阅读更多...
linux ftp日志_linux学习笔记（一）——Linux分区和目录结构

linux ftp日志_linux学习笔记（一）——Linux分区和目录结构

linux学习笔记&#xff08;一&#xff09;——Linux分区和目录结构安装Linux时&#xff0c;手动挂载分区的情况下&#xff0c;/ 和 swap 是必须要挂载的&#xff0c;其他/home、/boot 等可以根据需要自行挂载。一般来说&#xff0c;简单的话&#xff0c;建议挂载三个分区&#…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023