计量经济学模型是从统计学模型中衍生出来的,故将它们一并放在此处进行说明。
实际上,很多人在很久之前就督促我写一篇统计学和计量经济学模型的文章,但我太懒惰,一直拖到现在,也是十分汗颜。
先讲一些统计学上的基础故事,主要以猪重估计与沉船搜索为例吧。某个地区每年举办一次猪的重量的竞猜活动,与真实重量最接近的人获得奖金。数学家将这些五花八门的竞猜数据进行统计,发现其平均值与真实值几乎相等。第二个例子说的是打捞沉船的事情,让多个团队进行设想,并估计船只沉的过程及沉落地,然后将所有的结果进行统计,所得的地点与沉船实际地点很近。
可以看出,统计学还是有一定的意义的。上述的两个事例仅仅说明了单变量比较准确。实际上,多个变量之间也存在着一定的因果关系。这种情况下,统计学描述这一问题准确吗。
统计学在这个问题上借鉴了映射的概念,而其中最重要的是函数/方程关系,最简单的莫过于线性。比如假定一个变量x是另一个变量y的原因,在线性思维的基础上,这两个随机变量大致满足下列的形式
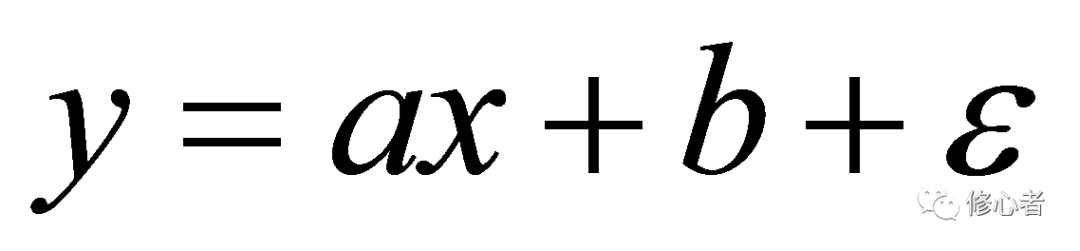 (1)
(1)
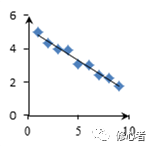
由于y与x均是随机变量,实际测定的数组(x,y)总不落在直线y=ax+b上,而是围绕着这个直线上下波动。
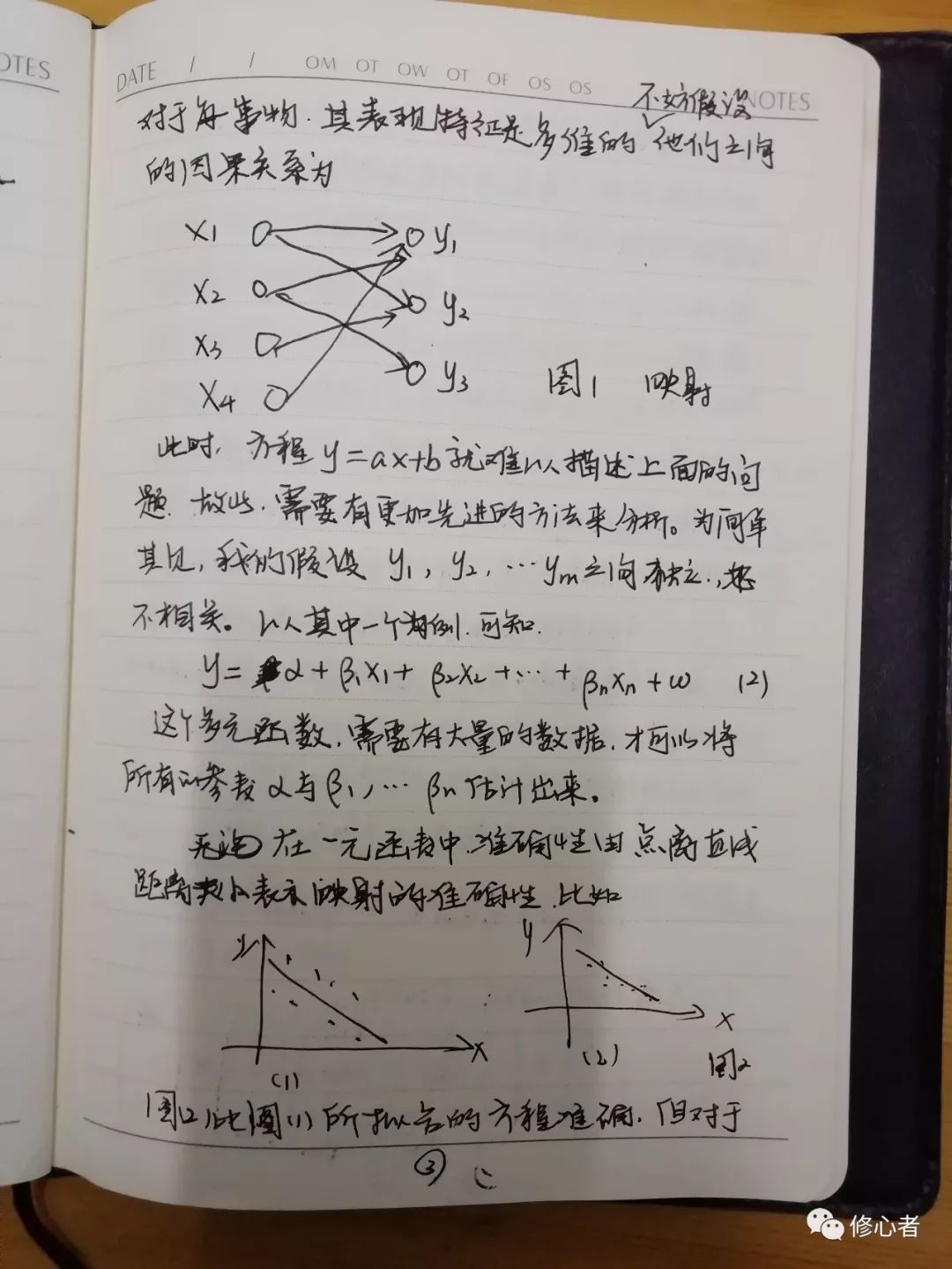
当然,线性化假设不能描述事物的本质,我们往往处在一个非线性的社会之中,非线性现象比比皆是。另外,经济与管理中,存在着大量的非函数映射关系,这个显然是y=ax+b无法解释的。更进一步的,经济与管理中不是两个变量所决定的,而是由多个变量所决定,对于每一事物,其表现特征是多维的,不妨假设它们之间的因果关系为
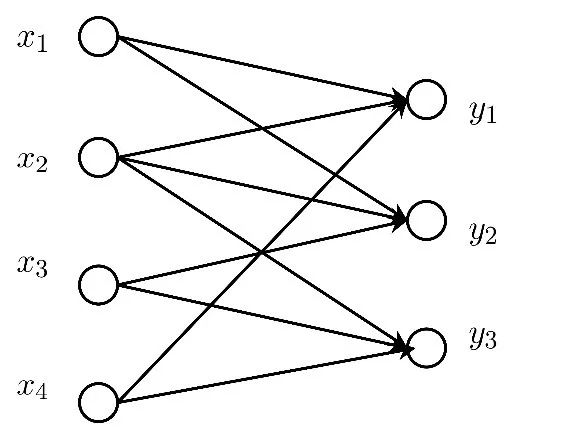
图1映射
此时,方程y=ax+b就难以描述上面的问题。故此,需要有更加先进的方法来分析。为简单起见,我们假设y1,y2,……ym之间独立,互不相关。以其中一个为例,可知
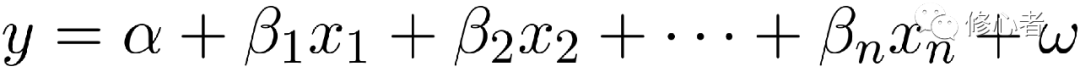 (2)
(2)
这个多元函数,需要有大量的数据,才可以将所有的参数 与,……估计出来。
在一元函数中,由点离直线距离表示映射的准确性。比如
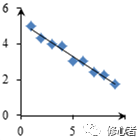
(1) (2)
图2
图(2)比图(1)所拟合的方程准确。但对于多元函数来说,这个参数在什么情况下是正确的,则成为统计学家与计量经济学家所关注的重点问题之一。一种叫最小二乘法的估计方法——当然是最简单的、最粗糙的方法,确定参数的大小——参数的准确性决定了方程的准确性。计量经济学或多元统计学中对于最小二乘法的讲解异常晦涩,很少有人能理解。今天,我们一改之前的文风,在此处花一点点笔墨,讲一下这个最小二乘法。
不妨假定获取了m个样本的数据,假定每个样本基本上服从
则有
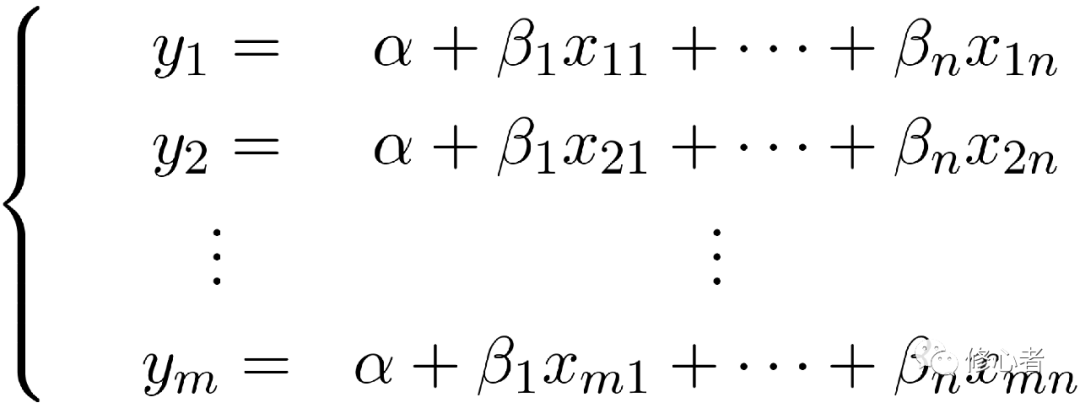 (3)
(3)
写成矩阵的形式,可知
 (4)
(4)
假定ω服从N(0,1),则有
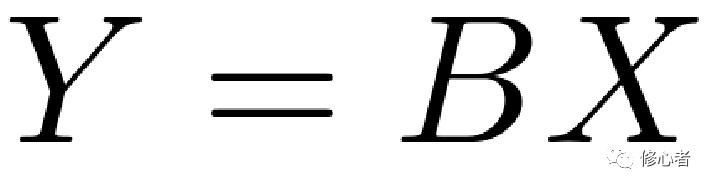 (5)
(5)
现在已知X与Y、B未知,故做以下的变换,便可得到B的值
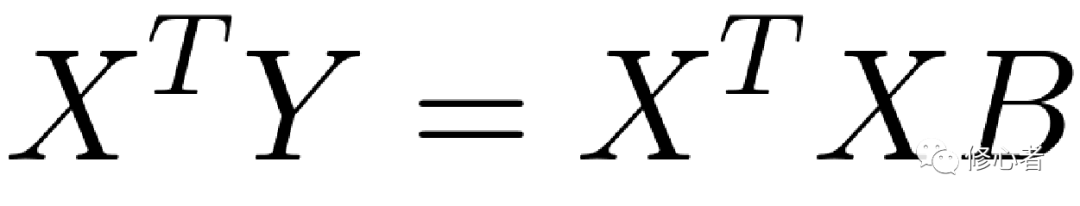 (6)
(6)
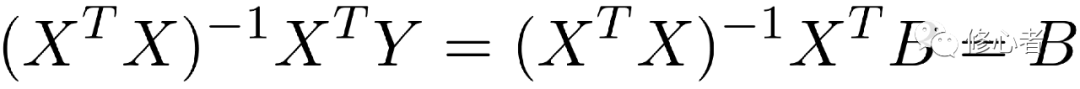 (7)
(7)
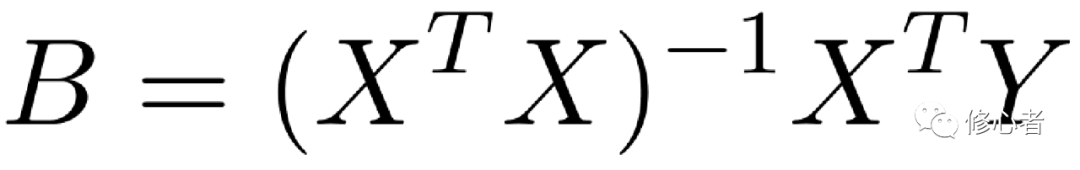 是最小二乘法的本质,其余的,如加权最小二乘法,便是在此基础上的拓展。在好的估计方法之下,方程的准确性便会增加。
是最小二乘法的本质,其余的,如加权最小二乘法,便是在此基础上的拓展。在好的估计方法之下,方程的准确性便会增加。
正如前文所述,还有更多的非线性关系,那么这种关系的多样性与复杂性决定了统计或计量的多样性与复杂性,我们关注线性关系的主要原因并不是线性分析的简单性,还是因为很多事物可以转化成线性的,以著名的生产函数为例,
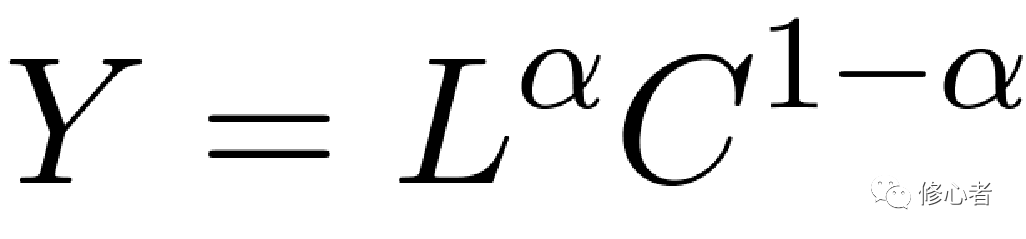 (8)
(8)
就可以转化成线性方程
 (9)
(9)
我们称之为无标度性,或幂律分布。无标度是一个经济与管理中非常著名的特征。正如在《规模》中所述的,世界万物都可以归结为这种属性。不过最关键的是要找到这些变量,一旦发现了这些变量以及这个对应的关系,就有重大的发现。然而,最困难的是发现这些变量,一般情况下这种变量很难找到,不仅需要对所研究对象非常熟悉,而且需要大量的探索。唯有不断地探索、不断的失败,才能找到合适的变量。这种线性关系不仅在数学上成立,更应该在实际中找到对应的因果关系。
无标度性,也称标度不变性,指的是对自变量坐标进行任意的拉伸或压缩后,函数的表达形式不变,即
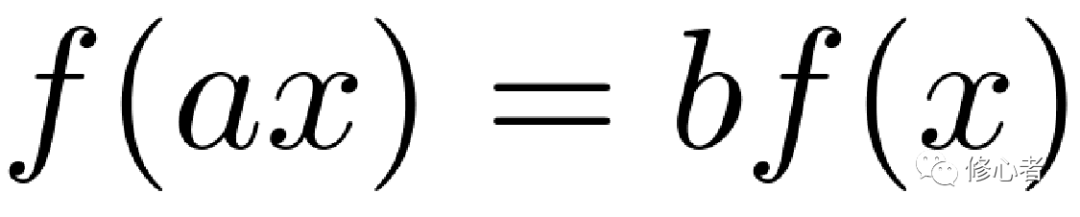 (10)
(10)
而这种形式,仅有幂函数满足它。不妨令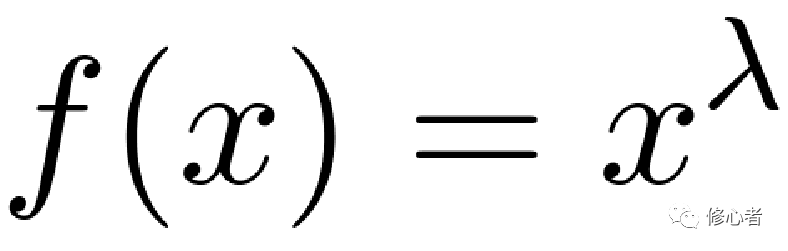 ,则有
,则有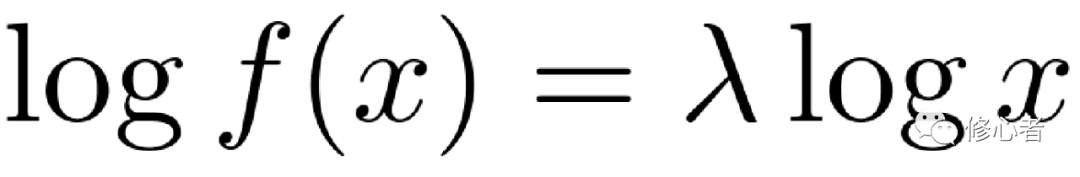 ,恰好满足这个直线关系。
,恰好满足这个直线关系。
然而在统计学或计量经济学的模型中,也并非仅仅有这一种映射(函数)关系,还有更多的模型等着我们去探索。让我们以生命周期理论为主,分析一下经济组织的一般发展机制,在事物发展变化过程中,我们一般认为可以分成若干个阶段。不同阶段中,它的影响因素不同——此处的不同不仅仅局限于量的不同,而且还会包括因素种类的不同。在事物刚刚发展(比如初建企业)之时,它能否成长的原因在于产品本身以及企业努力,此时关注了企业的经营,但当事物成熟之后,对其发展起决定作用的则在于管理,尤其是在发展的制度。可见它的因素会不断变化。如果新研究的问题恰好处于成长与成熟的中间状态——我们称之为“接续态”,则因素的变化非常明显,模型会变成
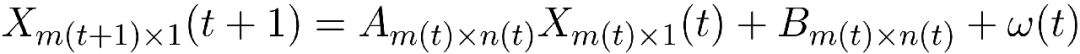 (11)
(11)
这其中就描述了影响因素的变化性。如果碰到此类问题,就需知道哪个状态变化(拐点)的时间,以及在切换过程中因素的变化情况,如下图所示:
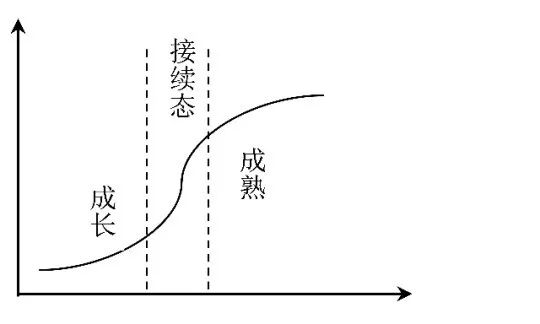
图3
如上图所示,在接续态有一个下限与上限,在此区域中,关键因素的切换非常快,也许在前一时刻还是主要的影响因素,在下一刻就会成为次要的因素,反之亦然。
这个过程中的统计模型实际上非常难构建。为了方便分析,在接续状态一般会考虑所有的因素,即使次要因素的影响不显著,也不应在意,也许在下一个时刻就显著了呢。在这个“接续态”中,方程在不断的变化,主要体现在参数不断的变化。这个变化一般有三种:j围绕一个数值上下随机波动,但不能超过某一个界。k是一个随机变量,但受到近期影响力度强于远期的影响,也就是说,每个时间点的系统特征对后续都有影响。离得越近的系统对其影响越大,如股市属于此类。③参数是一个随机过程,且参数之间构成一个鞅差序列—这种情况最为复杂。在混沌状态下,经济与管理系统就具备这种性质。那么,对于这个系统的统计意义上的模型,最有效的估计方法有LMS与卡尔曼滤波。这种时变随机结构的系统更能体现经济系统的复杂性与随机性。
让我们退回来,回到统计模型的多样性上。多元统计除此之外,还有大量的其他模型。计量经济学在此基础上更是推出了形形色色的模型,这些所谓的一个又一个的模型,让分析者的选择难度变得更大。
首先,在这一类模型中,除了连续性变量,也有分类变量、序类变量。不妨假设我们考虑他们,一般的做法是加入一个虚拟变量——哑变量作为参考值,而当与另一种情况进行比较,值得注意的是,一旦建立一个参考——参照物,我们必须弄清这个分类变量的性质—既有无“序”的出现——此处的“序”很关键。进一步来说,当各个类型之间属于平等时,用虚拟变量会让模型变得有意义。但如果不平等,有一些等级关系时,情况则变得更复杂。事实上,当分类变量作为解释变量、控制变量时,我们在做统计模型的时候,相当于提前对总体行为分类,针对每一类型来说,做出的一个对应模型。一般讲,对于关系“平等”的分类变量来说,其最终效用的差异主要体现在类型的差异上,与其他连续型变量关系不大。如果这其中有一些序关系的存在,则在其他连续型变量的影响会截然不同。
举例来说,如果我们的分类变量有一个是“贫富”,而资源获取能力、社会关系的强弱影响会差异很大。对于穷人来说,显然钱比关系重要,但对于富人来说,关系比钱重要。他们获利能力的差异性就很强。如果用经典意义上的分类变量处理方法建模,必将得到一个错误的结果。
当这些分类变量变成被解释变量时,就会衍生出几个模型、Logistic模型、Probit模型、Multi-Logistic模型,这种概率选择模型在近几年被大量的应用,甚至是错误的应用。一般的,某种形式被选择需依赖于一些因素。如果知道某一经济体这些因素的特征,就可以测算出选择特定状态的被选的概率大小。而Probit模型与其他两者最大的区别在于,Probit的被解释变量属于有序分类变量,而Logistic与Multi-Logistic的被解释变量属于无序分类变量。对于Probit模型的分析,难度远远大于其他两者。
无论是Logistic,还是Probit模型,我们都称之为非线性模型。不过这种非线性模型是比较简单的非线性模型,而不是真正的非线性模型,并且这个模型是确定的,而非随机的。
当然,还有一些非线性统计模型,鉴于篇幅原因,不作释解,仅仅提下。
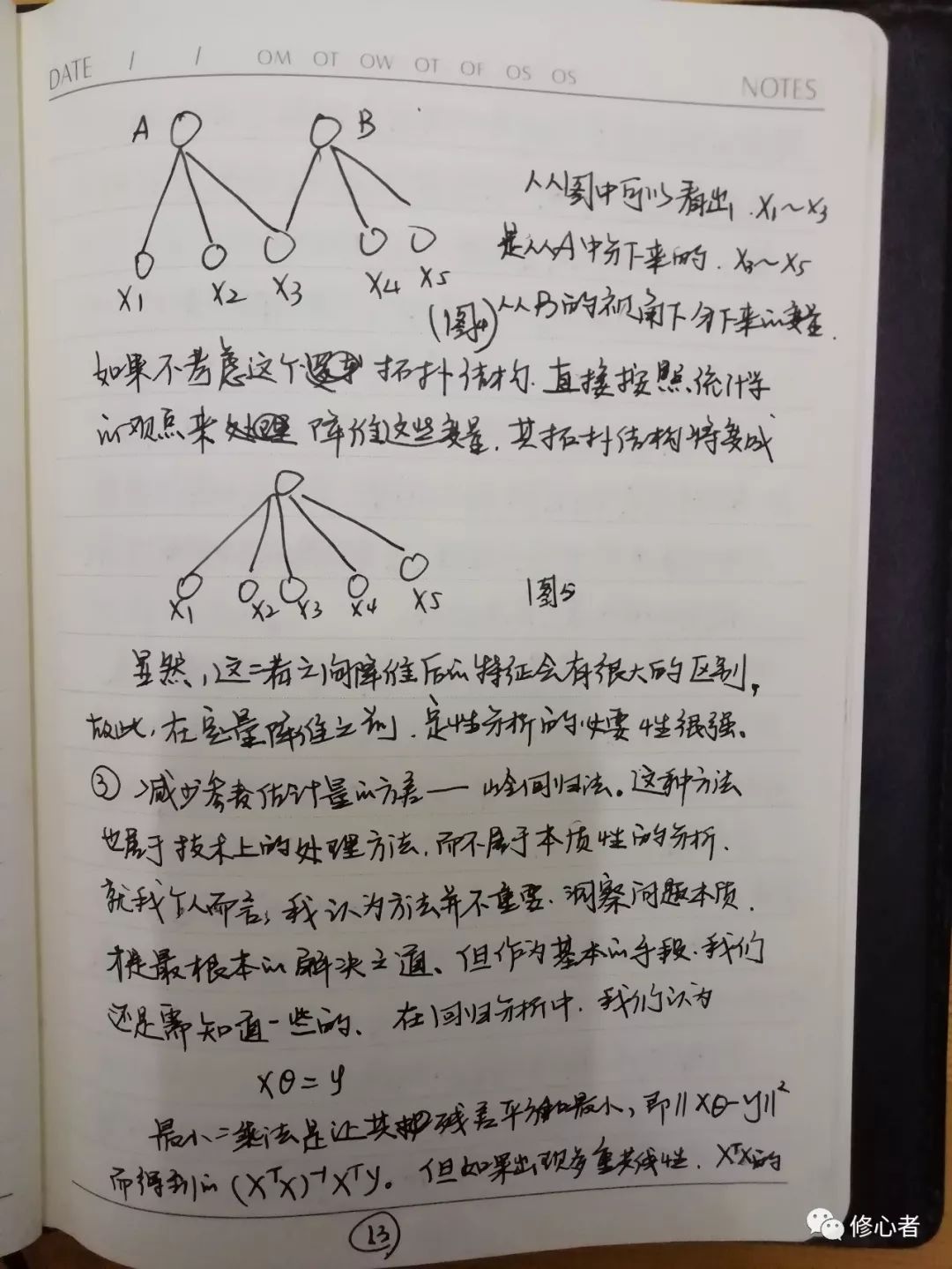
统计学与计量经济学中的基本条件中有一个非常重要,叫多重共线性。多重共线性的本质原因是对管理与经济系统的性质不清。这时只好把所有能考虑的因素都考虑上。一般的做法有几种:①降维:用逐步回归的做法,将不重要的变量逐个删掉,观测结果的准确性,直到删一个变量之后模型的结果发生显著变化为止,这个工作量极其大。在功利主义盛行的今天,“浮躁”与“学术造假”之风不断的几天,很少有人认真的做研究,也不会有人认真的选择了。②主成分分析/因子分析,将二者放在一起说明,其实也不是很恰当,毕竟这是统计学中一种比较偷懒的方法。然而,在数学上有道理,在经济与管理中不一定行得通,这主要是因为,在经济与管理中,不同类型的变量可以再细分,但他们属于同一个“父辈”,如果能找到这种逻辑关系,主成份分析/因子分析才有意义。见下图
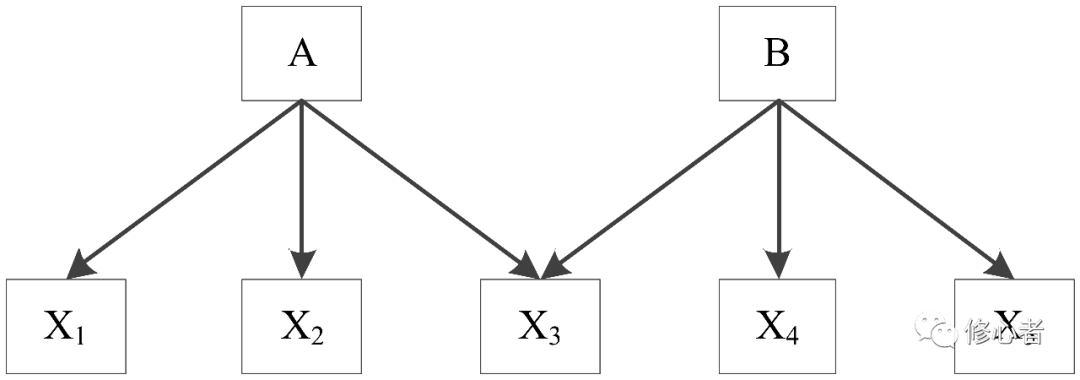
图4
从图中可以看出x1~x3是从A中分下来的 x3~x5从B的视角下分下来的变量。如果不考虑这个拓扑结构,直接按照统计学的观点来降维这些变量,其拓扑结构将变成
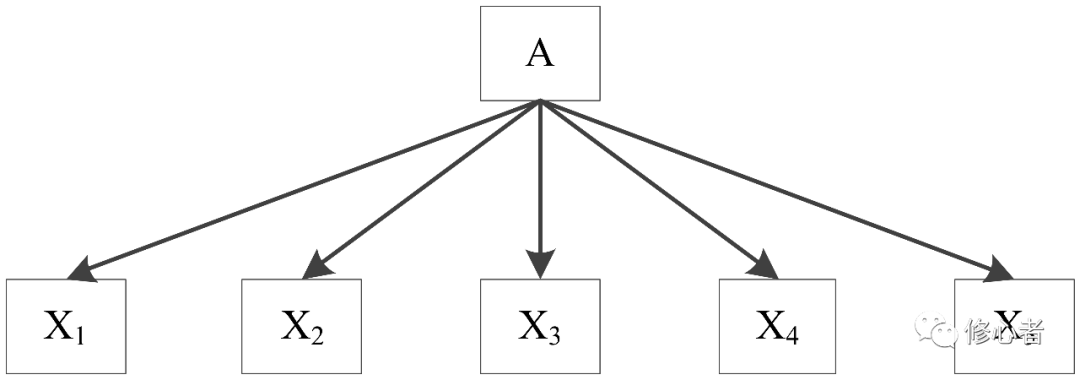
图5
虽然,这二者之间降维后的特征会有很大的区别,故此,在定量降维之前,定性分析的必要性很强。③减少参数估计量的方差——岭回归法。这种方法属于技术上的处理方法,而不属于本质性的分析。就我个人而言,我认为方法并不重要,洞察问题本质才是最根本的解决之道,但作为基本的手段,我们还是需知道一些的,在回归分析中我们认为
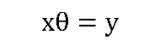
最小二乘法是让其残差平方和最小,即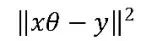 而得到的
而得到的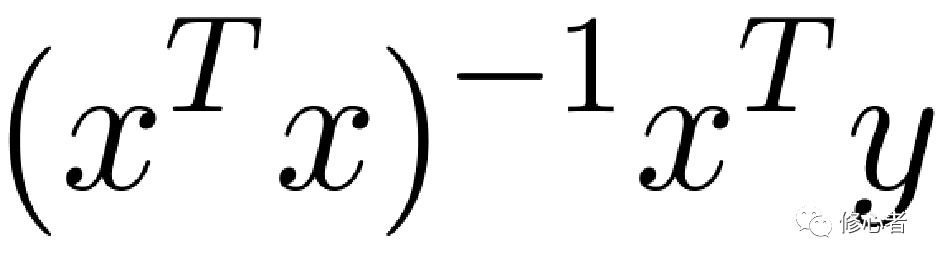 。但如果出现多重共线性,
。但如果出现多重共线性,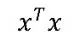 的行列式接近于0,则为一个不适定问题。岭回归的做法就是将这个“不适定”问题转换成“适定”问题:为损失函数加上一个正则化项。
的行列式接近于0,则为一个不适定问题。岭回归的做法就是将这个“不适定”问题转换成“适定”问题:为损失函数加上一个正则化项。
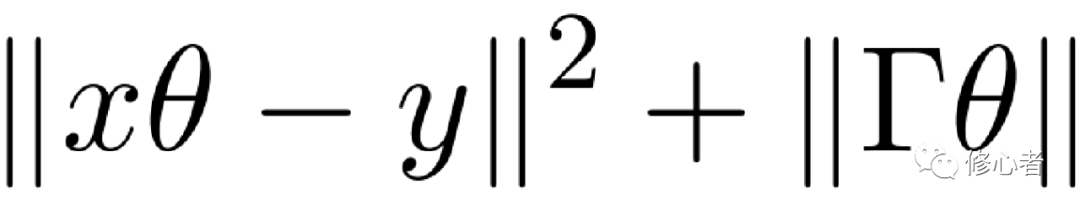 , 其中
, 其中 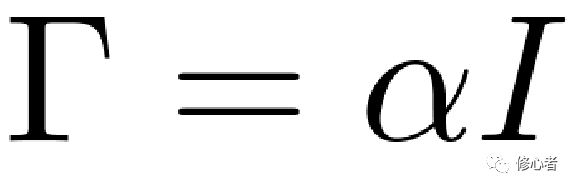 (12)
(12)
故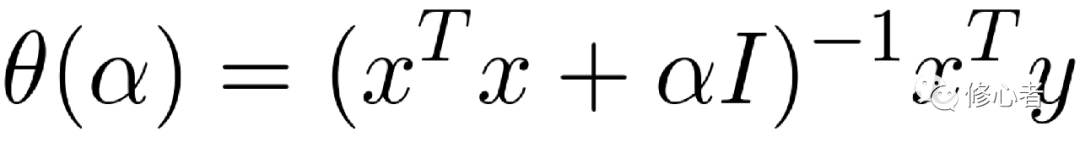 ,其中
,其中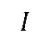 为单位矩阵。从上面可以看出,岭回归从本质上并没有解决解释变量相互解释的现象,反之是从数学手段上对其进行了一定的处理。当系统属性不明确时,我们可以用此类方法来处理。
为单位矩阵。从上面可以看出,岭回归从本质上并没有解决解释变量相互解释的现象,反之是从数学手段上对其进行了一定的处理。当系统属性不明确时,我们可以用此类方法来处理。
当然,变量之间相互解释的观察并不一定要死守看经典的模型。我们可以选择SEM(结构方程模型)来处理这一问题。不过需注意的是,SEM模型对定性分析的要求非常高。
统计学或计量经济学都要求有足够的样本做支撑。如果样本量较少怎么办?科学家构成了一个SVMC(支持向量机)模型,这个模型可以解决对应的问题。
总之,由于得到充分的发展,统计学的计量经济学中还有大量的静态模型,由于篇幅有限,我们不做一一介绍。我们主要是介绍这一类模型的思想、思维,并不局限于方法的说明。如有兴趣,不妨去查阅专业的资料。
其实,要准确刻画事物的特征,就应加入时间的因素,让这些个静态的模型“动”起来。在统计学或计量经济学时,时间这一因素已被重视,尤其是单一变量的时间序列过程。已得到非常全面的描述,在本文中不再啰嗦。在下文中,我们将提出“时滞”的思想。
假设经济与管理的问题可由一组变量所描述,这种描述可以分成两种情况。一是刻画特征。二是描述内在机制。无论哪种,都将面临着以下三种类型的变量。①即时刻画/影响经济与管理系统状态属性的变量,我们称之为一致性指标/因素②提前一段时间就可以刻画/影响经济与管理系统状态属性的变量。我们称之为先行性指标/因素。这类具有预兆性的变量往往在事物发展之前就会影响管理系统的特征③滞后一段时间才会刻画影响经济与管理系统的属性,我们称之为滞后指标/因素,这句话似乎有问题,但你没听错,的确是这样的。比如说,我们要评价某个科学家的科研实力,用一致性指标所得的结果远没有利用滞后性所得的结果的准确。因为科学研究结果是真是假需要实践来验证。同样的,未来可能的因素会影响该经济/管理系统的属性。比如说,中国在20年之后的人口结构(以年龄为参考点)将严重影响目前消费产品与服务结构的决策。故此,该模型将变成下面的形式。
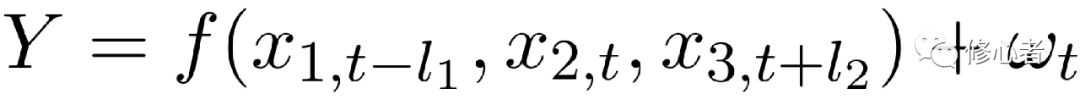 (13)
(13)
其中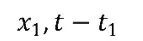 、
、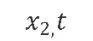 、
、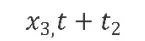 分别表示,先行型指标/变量、一致指标/变量、滞后型指标变量。l1 和l2分别表示先行周期与滞后周期、l1 与l2是一个正数,故此对x1、 x2与x3的识别与构造,以及l1 与l2的确定则显得尤为重要。对于前者,我们在前文中的很多篇幅中有提过。但对于l1 与l2的确定。则需要进一步的定性定量分析。事实上,也有成形的相关理论对此进行分析,建议有兴趣的读者自行查阅。
分别表示,先行型指标/变量、一致指标/变量、滞后型指标变量。l1 和l2分别表示先行周期与滞后周期、l1 与l2是一个正数,故此对x1、 x2与x3的识别与构造,以及l1 与l2的确定则显得尤为重要。对于前者,我们在前文中的很多篇幅中有提过。但对于l1 与l2的确定。则需要进一步的定性定量分析。事实上,也有成形的相关理论对此进行分析,建议有兴趣的读者自行查阅。
如果方程(13)具有参数随机时变的特征,则用最小二乘法、加权最小二乘法等经典的算法难以对此进行估算。此时LMS算法及Kalmman滤波大有作为了,甚至是更加先进的启发式算法。比如蚁群算法。
在前面的内容中,我们的变量都是结构性的变量,那么,如果这些变量是图片、音频、视频和文字,我们则想知道,统计学模型还适用吗?答案是肯定的,多维统计学习则是一种有效的工具,比如深度神经网络模型,其中的变量就可以是非结构化的数据,关于深度神经网络,我们将在后文中进行阐述,此处不再多说。
上面的分析,主要针对的是函数和方程,然而在经济与管理的问题中,更多的是映射。即图1所述,这种情况下,问题会更加复杂,对于这一问题,结构方程,深度神经网络都是一个比较有效的工具。对于神经网络所存在的梯度消失或梯度爆炸、训练太慢、过拟合等三大缺陷,引入无监督学习算法大大提高了效率,从而使得神经网络应用非常普遍。它是对映射解决的一种较为有效的模型,通过对大量的案例(样本)的学习,我们就可以得到各个节点中的权重,这个权重描述由输入到多输出之间的映射属性,然后在训练成功的基础上,对未知的事件进行分析,以便得到未知事件的性质。
在多维统计学习中,还有一些其他的方法。都会在经济与管理的科学研究中发挥巨大的功能,比如人工智能。正如我们在《大数据是思想,是思维还是方法?》一文中所讲的,目前最关键的是对各种算法进行严密的证明,如果能突破若干个基本问题,则会大大推动这一领域的发展。
鉴于篇幅有限以及本文的目的,我们不再花大量的笔墨分析各个模型,在这里我们将重点讨论如何使用这些模型,以及如何正确使用模型。换句话说,我们不应该为了模型而模型,以及不应该被模型绑架。首先我们必须关注统计学和计量经济学的使用条件,不是所有的问题都可以用它来解决,比如优化、博弈、动力学、复杂网络、概率,都无法用统计学和计量经济学去解释。其次,统计学的回归分析中——目前计量经济学也在关注这一块儿,其解释变量必须满足的几大条件,比如样本的随机性,变量的独立同分布性,噪声也有要求。然而在我们日常的研究例子中,很少有人完全做到这三大要求。比如样本的随机性在研究中就很难实现,因为我们数据的可获得性较差所致。毕竟这个不等同于随机实验,无法随心所欲的得到数据,故此很多科学家便依赖于统计年鉴和问卷调查。而依赖于某种数据时,本身便失去了随机性。比如,有人研究中国的企业创新问题,但只能获取A股企业的数据,没有未上市的企业以及众多的未上市的中小企业。那么,对于技术创新本身来讲,到底是中小企业创新的多,还是上市企业创新得多,这本身就需要论证。如果仅仅采用上市企业的数据,那么未上市企业则被排除,这个悖论应该是一个很好的切入点。一旦选择A股企业,那么选择企业时,很多人都会选择竞争力在前百分之X的企业。显然,这个选择并不是随机选择,而是典型分析,不符合统计分析与计量经济学的思想,所得的结论也会有所偏差。现在分析第二个条件:在分析时大都要求变量满足独立同分布的条件。在这点上,大家做的都不太好。下面举几个例子,首先变量的类型不一致,在其中有效益变量,也有成本性变量,还有居中型变量。在分析的过程中都应该把变量化成效益型变量。成本型和居中型变量的转化方法分别如下:
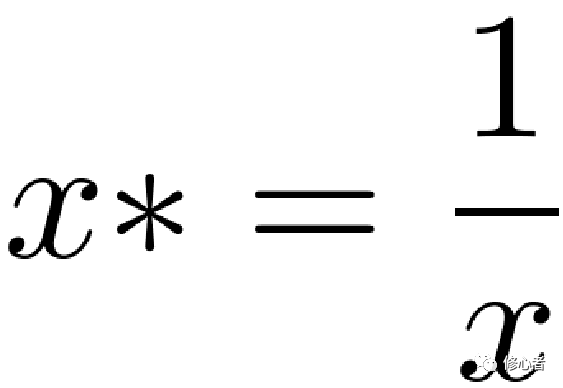
 (14)
(14)
这里,假定居中型变量的曲线如图6:
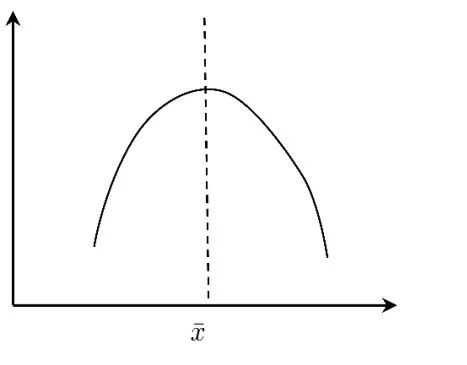
图6
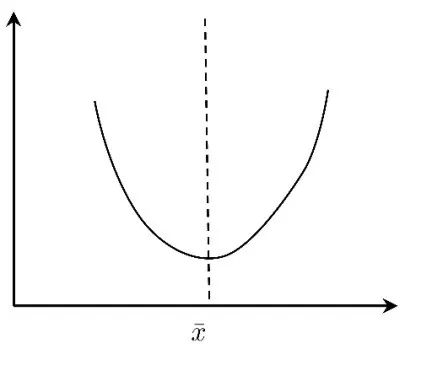
图7
对于图7的情况则恰好相反,其中很多科研工作者都不对变量进行无量纲化处理,而这个更为重要,当且仅当量纲去掉之后,统计模型才准确可靠。再次,他们也没有进行标准化处理,将所有的变量变成0-1之间的一个数。第四,所有很多经济与管理学家在做研究时喜欢采用问卷调查的方法,而在问卷调查中会涉及到很多分类变量,并且有一定的无序分类变量,比如性别,民族,地域,然后很多人就用这些数据进行回归分析。显然这是一种错误的做法,举例来说,设0=男,1=女,那么他们只能以分类变量进入回归模型中,而不能直接放入。毕竟1>0,但女男。
即使对于有序分类变量,我们也不能随便的采用直接回归,而应当进行适当的处理。再进一步来说,在分析中,自变量必须有且至少有一个连续变量才可以得到正确的结论。因为有序分类变量的组内方差、组间平方差以及总平方差都无法找到。这些科学家混淆了回归分析中的那个最小二乘法的内涵,它只能针对连续变量,对于离散变量则不会如此处理。
在统计学中,噪声一般都假设为一个白噪声,因为所有的变量都假设是一个服从特定分布如正态分布的随机变量,所以多个变量的联合分布也服从正态分布的假设。然而,在实际中,这个噪声并不是白噪声,而是一个彩噪声,我们对于其分析也有类似的处理。详情可查阅对应的资料。
我应该关注每一个模型的适用条件,这一点非常关键,知道每个模型的前因后果才能把我们的问题抽象成和对应的模型,这些在前文已已有涉及,在此不再累赘。其实我们知道每一个模型都蕴含着一种思想,模型本身的思想思维过程的重要性远远大于形式以及其参数估计方法。
关于统计与计量经济学中的一些问题,我们先谈到这里,文章不能将所有的内容都一一详述,只能从其思想,思维及模型自身做一点点见解,试图达到抛砖引玉的效果。望对读者有所启示,最后祝在此领域中的各位研究学者出来更多的优秀成果。





























public、protect、private继承方式 C++)

)


)

)
(转))


