目录
- 【1】NN复杂度
- 【2】指数衰减学习率
- 【3】激活函数
- 优秀激活函数所具有的特点
- 常见的激活函数
- 对于初学者的建议
- 【4】损失函数
- 【5】缓解过拟合——正则化
- 【6】参数优化器
- 【1】SGD
- 【2】SGDM(SGD基础上增加了一阶动量)
- 【3】Adagrade(SGD基础上增加了二阶动量)
- 【4】RMSProp(SGD基础上增加了二阶动量)
- 【5】Adam(同时结合SGDM一阶动量和RMSProp的二节动量)
- 优化器对比总结
【1】NN复杂度
空间复杂度:
层数:隐藏层层数+输出层
总参数:总w+总b
时间复杂度:
乘加运算次数
以下图为例:总参数=3x4+4(第一层) +4x2+2(第二层)=26
乘加运算次数=3x4+4x2=20

【2】指数衰减学习率
已知:学习率过小,收敛速度慢。学习率过大导致不收敛。
可以先用较大的学习率,快速得到较优解,然后逐步减小学习率,使模型在训练后期稳定,例如指数衰减学习率。
指数衰减学习率=初始学习率*学习率衰减率^(当前轮数/多少轮衰减一次)
epoch = 40
LR_BASE = 0.2 # 最初学习率
LR_DECAY = 0.99 # 学习率衰减率
LR_STEP = 1 # 喂入多少轮BATCH_SIZE后,更新一次学习率
for epoch in range(epoch): # for epoch 定义顶层循环,表示对数据集循环epoch次,此例数据集数据仅有1个w,初始化时候constant赋值为5,循环100次迭代。lr = LR_BASE * LR_DECAY ** (epoch / LR_STEP)
【3】激活函数

对于线性函数,即使有多个神经元首尾相接构成深层神经网络,依旧是线性组合,模型表达力不够。

MP模型比简化模型多了一个激活函数,它的加入加强了模型的表达力,使得深层网络不再是输入x的线性组合,而且随着层数增加提升表达力。
优秀激活函数所具有的特点
非线性:激活函数非线性时,多层神经网络可以逼近所有函数
可微性:优化器大多用梯度下降更新参数
单调性:当激活函数是单调的,能保证单层网络的损失函数是凸函数
近似恒等性:f(x)约等于x,当参数初始化为随机小值时,神经网络更稳定激活函数输出值的范围:
1、激活函数输出为有限值时,权重对于特征的影响会更显著,基于梯度的优化方法更稳定
2、激活函数输出为无限值时,参数的初始值对模型的影响特别大,要使用更小的学习率
常见的激活函数
1、sigmoid函数:
函数公式、函数图像与导数图像:
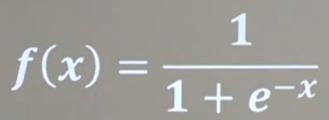 |  |
调用方法:tf.nn.sigmoid(x)
特点:
1、易造成梯度消失(输入的值较大时,梯度就约等于0了)
2、输出非0均值,收敛慢(我们希望输入每层网络的特征是以0为均值的小数)
3、幂运算复杂,训练时间长
神经网络最初兴起的时候,sigmoid函数作为激活函数用的很多,但是近年来用sigmoid函数的网络已经很少了。
因为,深层神经网络更新参数时,需要从输出层到输入层逐层进行链式求导,而sigmoid函数导数的输出范围是(0,0.25],链式求导需要多层导数连续相乘,这样最终导致输出为0,造成梯度消失,参数无法继续更新。
2、Tanh函数:
调用方法:tf.math.tanh(x)
特点:
1、易造成梯度消失
2、输出0均值
3、幂运算复杂,训练时间长
函数公式、函数图像与导数图像:
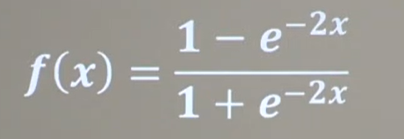 |  |
3、Relu函数:
函数公式、函数图像与导数图像:
 |  |
送入激活函数的输入特征是负数时,激活函数输出是0,反向传输梯度是0,经过relu函数的负数特征过多导致神经元死亡,我们可以改进随机初始化,避免过多负数特征传入,也可以通过设置更小的学习率,减少参数分布的巨大变化,避免训练中产生过多负数特征
4、Leaky Relu函数:
函数公式、函数图像与导数图像:
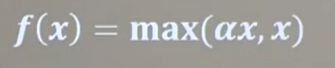 |  |
调用方法:tf.nn.leaky_relu(x)
理论上来说,leaky relu具有relu的所有优点,外加不会有deadrelu问题,但是在实际操作中,并没有完全证明leaky relu总好于relu
对于初学者的建议
1、首选relu激活函数
2、学习率设置较小值
3、输入特征标准化,让输入特征满足以0为均值,1为标准差的正态分布
4、初始参数中心化,让随机生成的参数满足0位均值,sqrt(2/当前层输入特征个数)为标准差的正态分布
【4】损失函数
NN优化目标:loss最小
常用三种损失函数:1、mse(均方差)2、自定义3、ce(交叉熵)
1、mse(均方差)
mse调用方式:
loss_mse =tf.reduce_mean(tf.square(y_-y))
预测酸奶代码:
import tensorflow as tf
import numpy as npSEED = 23455rdm = np.random.RandomState(seed=SEED) # 生成[0,1)之间的随机数
x = rdm.rand(32, 2)
y_ = [[x1 + x2 + (rdm.rand() / 10.0 - 0.05)] for (x1, x2) in x] # 生成噪声[0,1)/10=[0,0.1); [0,0.1)-0.05=[-0.05,0.05)
x = tf.cast(x, dtype=tf.float32)w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))epoch = 15000
lr = 0.002for epoch in range(epoch):with tf.GradientTape() as tape:y = tf.matmul(x, w1)loss_mse = tf.reduce_mean(tf.square(y_ - y))grads = tape.gradient(loss_mse, w1)w1.assign_sub(lr * grads)if epoch % 500 == 0:print("After %d training steps,w1 is " % (epoch))print(w1.numpy(), "\n")
print("Final w1 is: ", w1.numpy())
生成的系数确实约等于1
2、自定义损失函数
以销量预测为例:
均方误差损失函数默认认为销量预测多了、少了,造成的损失是一样的,其实不然。
预测多了:损失成本
预测少了:损失利润
若利润不等于成本,则mse产生的loss无法利益最大化!
可以把损失定义为一个分段函数
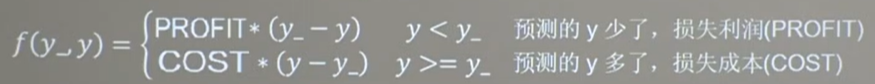
loss_zdy=tf,reduce_sum(tf.where(tf.greater(y,y_),COST(y-y_),PROFIT(y_-y)))
如:预测酸奶销量,酸奶成本(COST)1元,酸奶利润(PROFIT)99元。
预测少了损失利润99元,大于预测多了损失成本1元。
预测少了损失大,希望生成的预测函数往多了预测。
预测酸奶代码:(修改损失函数)
import tensorflow as tf
import numpy as npSEED = 23455
COST = 1
PROFIT = 99rdm = np.random.RandomState(SEED)
x = rdm.rand(32, 2)
y_ = [[x1 + x2 + (rdm.rand() / 10.0 - 0.05)] for (x1, x2) in x] # 生成噪声[0,1)/10=[0,0.1); [0,0.1)-0.05=[-0.05,0.05)
x = tf.cast(x, dtype=tf.float32)w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))epoch = 10000
lr = 0.002for epoch in range(epoch):with tf.GradientTape() as tape:y = tf.matmul(x, w1)loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * COST, (y_ - y) * PROFIT))grads = tape.gradient(loss, w1)w1.assign_sub(lr * grads)if epoch % 500 == 0:print("After %d training steps,w1 is " % (epoch))print(w1.numpy(), "\n")
print("Final w1 is: ", w1.numpy())# 自定义损失函数
# 酸奶成本1元, 酸奶利润99元
# 成本很低,利润很高,人们希望多预测些,生成模型系数大于1,往多了预测
生成的系数确实都大于1
3、ce(交叉熵)
调用方式:tf.losses.categorical_crossentropy(y_, y)
import tensorflow as tfloss_ce1 = tf.losses.categorical_crossentropy([1, 0], [0.6, 0.4])
loss_ce2 = tf.losses.categorical_crossentropy([1, 0], [0.8, 0.2])
print("loss_ce1:", loss_ce1)
print("loss_ce2:", loss_ce2)# 交叉熵损失函数
一般来说,输出先通过softmax函数使之符合概率分布,再计算y与y_的交叉熵损失函数,TensorFlow提供了同时计算的函数
tf.nn.softmax_cross_entropy_with_logits(y_, y)
# softmax与交叉熵损失函数的结合
import tensorflow as tf
import numpy as npy_ = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 0, 0], [0, 1, 0]])
y = np.array([[12, 3, 2], [3, 10, 1], [1, 2, 5], [4, 6.5, 1.2], [3, 6, 1]])
y_pro = tf.nn.softmax(y)
loss_ce1 = tf.losses.categorical_crossentropy(y_,y_pro)
loss_ce2 = tf.nn.softmax_cross_entropy_with_logits(y_, y)print('分步计算的结果:\n', loss_ce1)
print('结合计算的结果:\n', loss_ce2)
【5】缓解过拟合——正则化
为什么正则化可以化解过拟合,先看看下面两个视频和讲解吧:
过拟合
正则化如何运行
正则化不舍弃特征,而是减少了特征变量的量级,从而简化假设模型。由于变量过多,我们事先并不知晓每个变量对结果的相关程度,也就是说我们不知道该缩小哪些参数,我们选择缩小所有参数,也就是给所有参数加上惩罚项(除了theta0变量)。
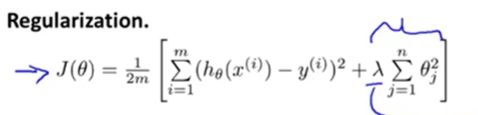
正则化参数λ用来控制两个不同目标之间的取舍:
1、更好地拟合训练数据
2、保持参数尽量地小
λ过大同样也会造成欠拟合的现象。
欠拟合解决方法:
1、增加输入特征项
2、增加网络参数
3、减少正则化参数
过拟合的解决方法:
1、数据清洗
2、增大训练集
3、采用正则化
4、增大正则化参数

示例:利用神经网络区分蓝色点和红色点

思路:
1、先用神经网络拟合出数据x1,x2,y_c的函数关系
2、生成网格覆盖这些点
3、将网格中坐标送入训练好的神经网络
4、网络为每个坐标输出一个预测值
5、将神经网络输出为0.5的预测值的线标出颜色,这线就是区分线
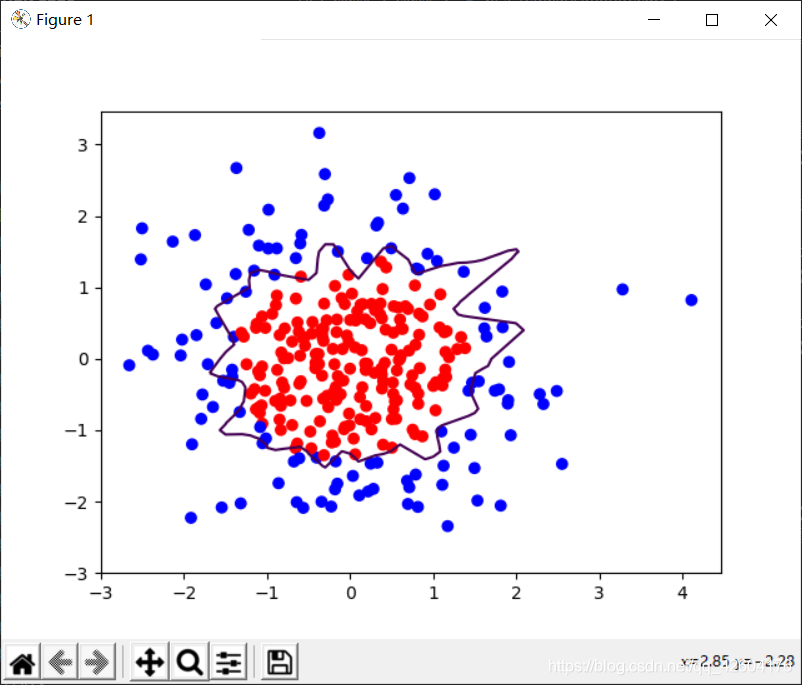
分别输出不正则化和正则化的效果,观察效果
左侧是正则化之前的,右侧是正则化之后的。
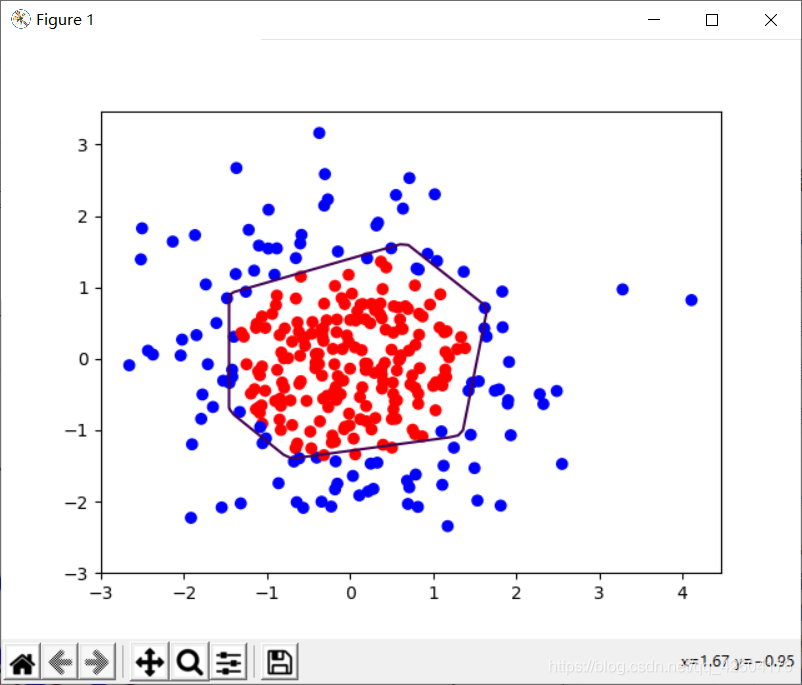 1层隐藏层,4个神经元 1层隐藏层,4个神经元 | 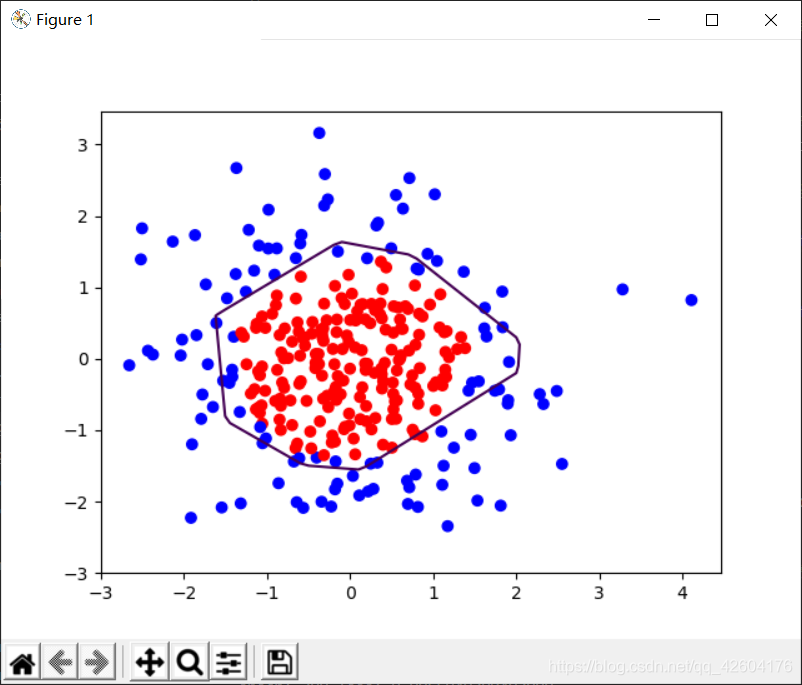 1层隐藏层,4个神经元 1层隐藏层,4个神经元 |
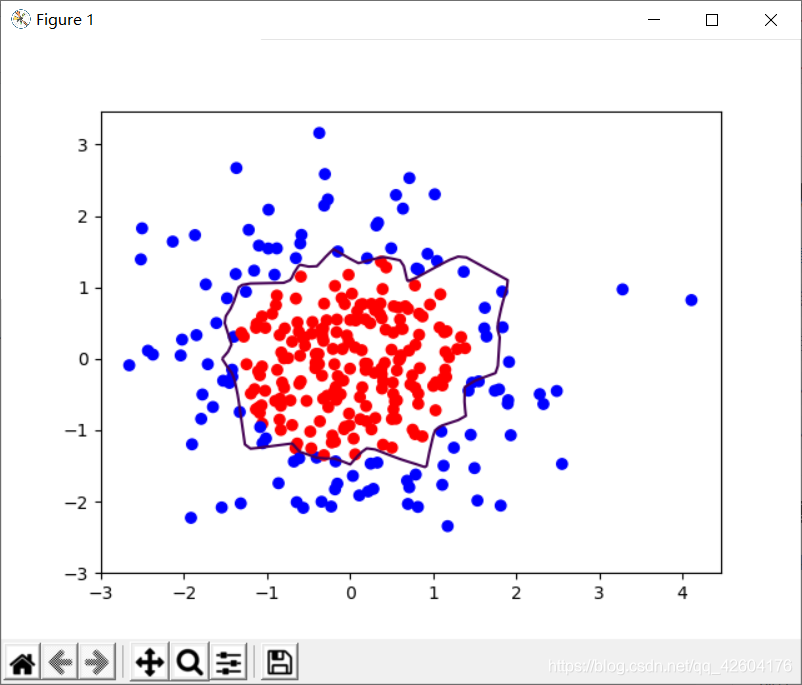 1层隐藏层,22个神经元 1层隐藏层,22个神经元 | 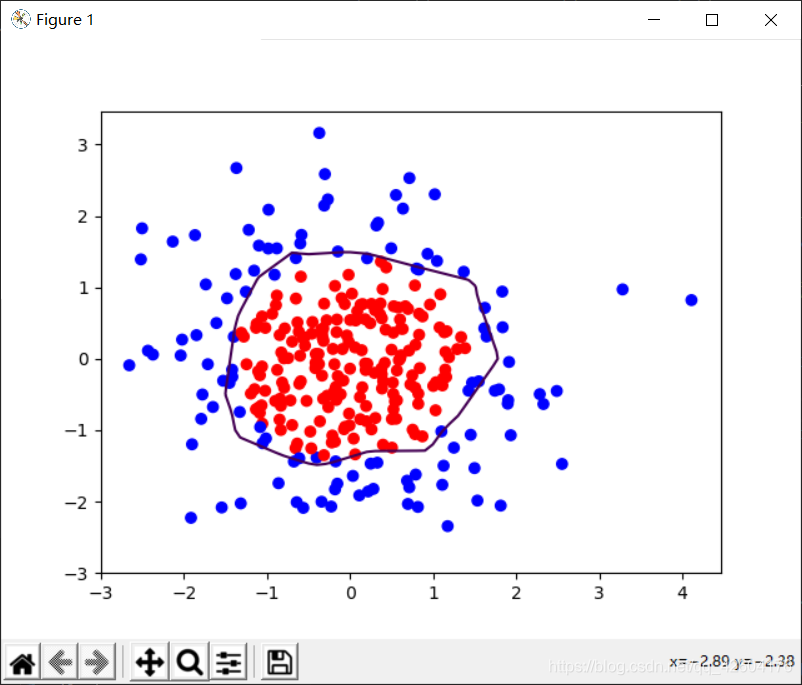 1层隐藏层,22个神经元 1层隐藏层,22个神经元 |
 1层隐藏层,40个神经元 1层隐藏层,40个神经元 | 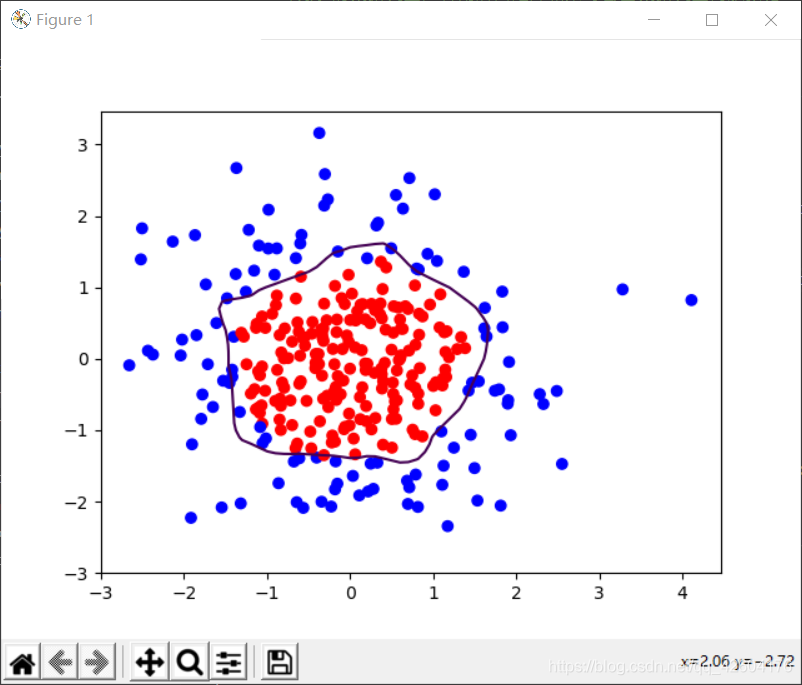 1层隐藏层,40个神经元 1层隐藏层,40个神经元 |
很明显地可以看出,加入L2正则化后的曲线更加平缓。有效缓解了过拟合。
【6】参数优化器
推荐链接
【基础算法】神经网络参数优化器https://zhuanlan.zhihu.com/p/97873519
MOOC神经网络参数优化器
参数优化器总体公式:

【1】SGD
公式: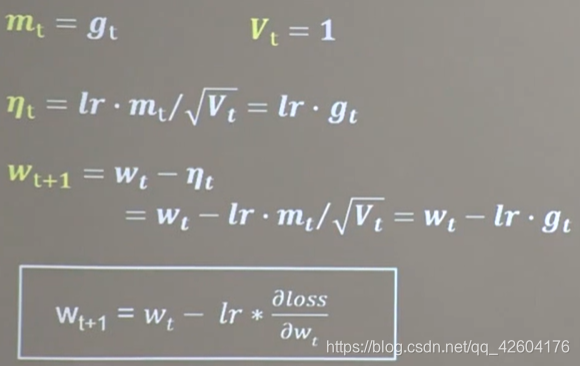
code:
# 实现梯度更新 w1 = w1 - lr * w1_grad b = b - lr * b_grad
w1.assign_sub(lr * grads[0]) # 参数w1自更新
b1.assign_sub(lr * grads[1]) # 参数b自更新
【2】SGDM(SGD基础上增加了一阶动量)
公式:
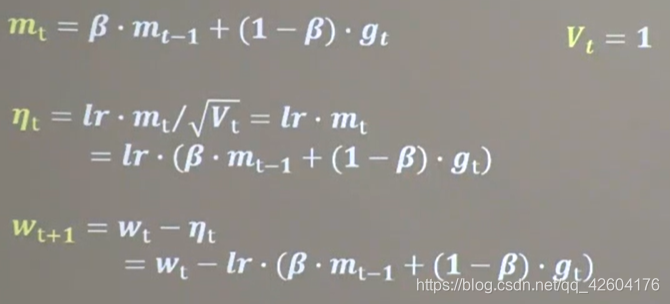
mt表示各时刻梯度方向的指数滑动平均值,表征了过去一段时间的平均值。β是接近1的超参数,一般等于0.9
code:
m_w, m_b = 0, 0
beta = 0.9# sgd-momentun
m_w = beta * m_w + (1 - beta) * grads[0]
m_b = beta * m_b + (1 - beta) * grads[1]
w1.assign_sub(lr * m_w)
b1.assign_sub(lr * m_b)
【3】Adagrade(SGD基础上增加了二阶动量)
公式:
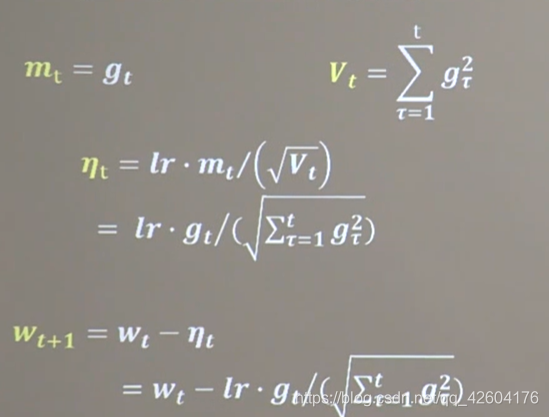
code:
v_w, v_b = 0, 0
# adagrad
v_w += tf.square(grads[0])
v_b += tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))
【4】RMSProp(SGD基础上增加了二阶动量)
公式:
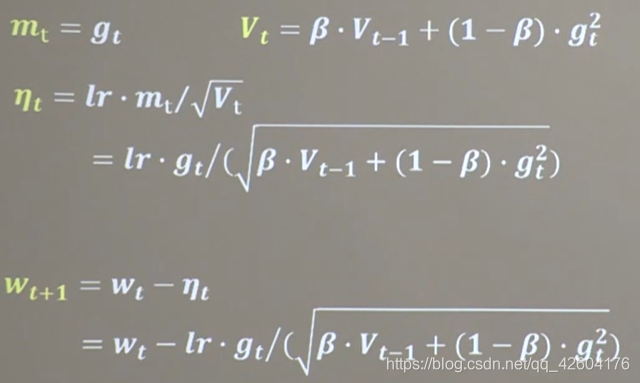
v_w, v_b = 0, 0
beta = 0.9
# rmsprop
v_w = beta * v_w + (1 - beta) * tf.square(grads[0])
v_b = beta * v_b + (1 - beta) * tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))
【5】Adam(同时结合SGDM一阶动量和RMSProp的二节动量)
公式:

code:
m_w, m_b = 0, 0
v_w, v_b = 0, 0
beta1, beta2 = 0.9, 0.999
delta_w, delta_b = 0, 0
global_step = 0
# adam
m_w = beta1 * m_w + (1 - beta1) * grads[0]
m_b = beta1 * m_b + (1 - beta1) * grads[1]
v_w = beta2 * v_w + (1 - beta2) * tf.square(grads[0])
v_b = beta2 * v_b + (1 - beta2) * tf.square(grads[1])m_w_correction = m_w / (1 - tf.pow(beta1, int(global_step)))
m_b_correction = m_b / (1 - tf.pow(beta1, int(global_step)))
v_w_correction = v_w / (1 - tf.pow(beta2, int(global_step)))
v_b_correction = v_b / (1 - tf.pow(beta2, int(global_step)))w1.assign_sub(lr * m_w_correction / tf.sqrt(v_w_correction))
b1.assign_sub(lr * m_b_correction / tf.sqrt(v_b_correction))
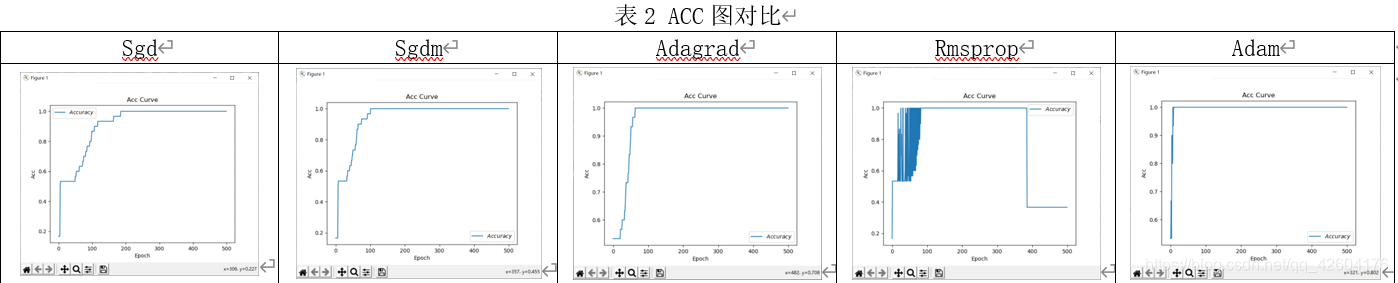
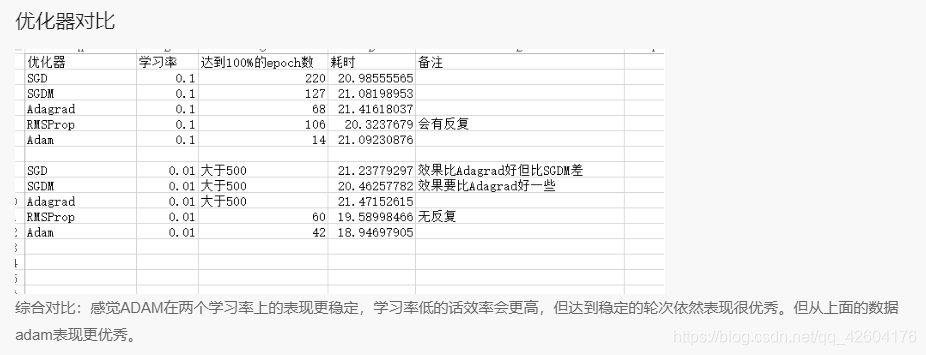
优化器对比总结
优化器对比(lr=0.1 epoch=500 batch=32)







方法)


:项目管理三大目标)



)

方法与示例)


之C语言程序设计复试笔试最后押题五套卷...)

