二叉树笔记（深度遍历与广度遍历+13道leetcode题目(深度3道、广度10道)）

本文章为结合leetcode题目以及公众号“代码随想录”的文章所做的笔记！
感觉代码随想录的题目整理真的很好，比自己盲目刷题好很多。

目录

  • 1、二叉树小记
    • 1、满二叉树与完全二叉树
    • 2、二叉搜索树
    • 3、平衡二叉搜索树AVL
    • 4、二叉树存储方式
    • 5、二叉树遍历方式
    • 6、二叉树的定义
  • 2、二叉树深度优先遍历递归算法书写
    • 1、leetcode144题：
    • 2、leetcode145题：
    • 3、leetcode94题：
  • 3、二叉树深度优先遍历迭代算法书写
    • 1、先序遍历（迭代法）
    • 2、中序遍历（迭代法）
    • 3、后序遍历（迭代法）
  • 4、二叉树深度优先遍历迭代算法格式统一
  • 5、二叉树层序遍历
    • 1、leetcode102:二叉树的层序遍历
    • 2、leetcode107:二叉树的层序遍历 II
    • 3、leetcode199:二叉树的右视图
    • 4、leetcode637:二叉树的层平均值
    • 5、leetcode429:N叉树的层序遍历
    • 6、leetcode515. 在每个树行中找最大值
    • 7、leetcode116. 填充每个节点的下一个右侧节点指针
    • 8、leetcode117. 填充每个节点的下一个右侧节点指针 II（遇上一题思路代码一致）
    • 9、104. 二叉树的最大深度
    • 10、111. 二叉树的最大深度

1、二叉树小记

1、满二叉树与完全二叉树

满二叉树：深度为k，有2的k-1个节点的二叉树。
完全二叉树：除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第h层，则该层包含1~2h个节点。

2、二叉搜索树

二叉搜索树是有数值的，是一个有序树。
它的特点：

1、若它的左子树不空，则左子树所有结点的值均小于它根结点的值
2、若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值
3、它的左右子树也分别为二叉排序树

3、平衡二叉搜索树AVL

AVL是一棵空数或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
C++中map、set、multimap、multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间复杂度都是logn。
而unordered_map、unordered_set、unordered_map、unordered_map底层实现是哈希表。

4、二叉树存储方式

链表存储与数组存储。
数组存储二叉树遍历：如果父节点的数组下标是i，那么它的左孩子就是i2+1,右孩子就是i2+2.

5、二叉树遍历方式

有两种遍历方式：
1、深度优先遍历：先往深走，遇到叶子结点再往回走
分为：前序遍历、中序遍历、后序遍历
这里的前中后，指的是中间结点的遍历顺序
前序遍历：中、左、右
中序遍历：左、中、右
后序遍历：左、右、中
深度优先遍历使用递归是比较方便的，可以借助栈使用非递归方式实现。

2、广度优先遍历：一层一层的去遍历
分为：层次遍历
广度优先遍历一般使用队列实现，利用了队列的先进先出的特点。这样才能一层一层的来遍历二叉树。

6、二叉树的定义

二叉树的定义和链表差不多，多了一个指针

struct TreeNode{int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x),left(NULL),right(NULL) {}
};

2、二叉树深度优先遍历递归算法书写

递归算法的三个要素：
1、确定递归函数的参数和返回值

若是在递归过程中需要处理某个参数，就在递归函数里面加上这个参数。
明确每次递归地返回值是什么，进而确定递归函数的返回类型

2、确定终止条件

1、如果在递归算法运行过程中出现栈溢出，大概率是终止条件写的不对
2、操作系统也是用一个栈的结构来保存每一层递归地信息，如果递归没有终止，操作系统的内存栈必然就会溢出

3、确定单层递归逻辑

确定每一层递归需要处理的信息。在这里也会重复调用自己来实现递归地过程

以前序遍历为例：
1、因为要打印出前序遍历结点的数值，所以参数里需要传入vector放在结点里的数据。没有返回值

void traversal(TreeNode* cur ,vector<int>& vec)

2、在递归过程中，如何算是递归结束？如果当前遍历的结点是空的，那么本层递归就结束了

if(cur == NULL) return;

3、前序遍历是中左右的循序，所以在单层递归中就要先取出中结点的数据

vec.push_back(cur->val);		//中
traversal(cur->left,vec);		//左
traversal(cur->right,vec);		//右

完整代码:

class Solution{public:void traversal(TreeNode* cur , vector<int>& vec){if(cur == NULL) return;vec.push_back(cur->val);traversal(cur->left,vec);traversal(cur->right,vec);}vector<int> preorderTraversal(TreeNode* root){vector<int> result;traversal(root,result);return result;}
};

中序遍历：

void traversal(TreeNode* cur , vector<int>& vec)
{if(cur == NULL) return;traversal(cur->left,vec);vec.push_back(cur->val);traversal(cur->right,vec);
}

后序遍历：

void traversal(TreeNode* cur , vector<int>& vec)
{if(cur == NULL) return;traversal(cur->left,vec);traversal(cur->right,vec);vec.push_back(cur->val);
}

1、leetcode144题：

给定一个二叉树，返回它的 前序 遍历。
示例:
输入: [1,null,2,3]
1

2
/
3
输出: [1,2,3]

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void traversal(TreeNode* cur , vector<int>& vec){if(cur == NULL) return;vec.push_back(cur->val);traversal(cur->left,vec);traversal(cur->right,vec);}vector<int> preorderTraversal(TreeNode* root){vector<int> result;traversal(root,result);return result;}
};

2、leetcode145题：

给定一个二叉树，返回它的 后序 遍历。
示例:
输入: [1,null,2,3]
1

2
/
3
输出: [3,2,1]

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void traversal(TreeNode* cur , vector<int>& vec){if(cur == NULL) return;traversal(cur->left,vec);traversal(cur->right,vec);vec.push_back(cur->val);}vector<int> postorderTraversal(TreeNode* root) {vector<int> result;traversal(root,result);return result;}
};

3、leetcode94题：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void traversal(TreeNode* cur , vector<int>& vec){if(cur == NULL) return;traversal(cur->left,vec);vec.push_back(cur->val);traversal(cur->right,vec);}vector<int> inorderTraversal(TreeNode* root) {vector<int> result;traversal(root,result);return result;}
};

3、二叉树深度优先遍历迭代算法书写

原理：为什么可以使用迭代法(非递归地方式)来实现二叉树的前后中序遍历？
递归地实现就是：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，
然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。

1、先序遍历（迭代法）

前序遍历：中左右；每次处理的是中间结点，先将根结点放入栈中，然后将右孩子放入栈中，再加入左孩子。
为什么要先加入有孩子，再加入左孩子？
这样出栈的时候才是中左右的顺序。
顺序如下：
在这里插入图片描述

class Solution{
public:vector<int> preorderTraversal(TreeNode* root){stack<TreeNode*> st;		//构建一个栈vector<int> result;st.push(root);			//先将根结点压入栈中while(!st.empty()){			//当栈中还有元素时TreeNode* node = st.top();	//将栈顶元素赋给新结点	st.pop();					//将栈顶元素出栈if(node !=NULL) result.push_back(node->val);	//如果这个结点不为空，将值赋给resultelse continue;									//否则继续，（也就是说如果结点为空不赋值）st.push(node->right);		//将该中结点的右孩子压入栈中st.push(node->left);		//将该结点中的左孩子压入栈中}return result;}
};

2、中序遍历（迭代法）

注意，前序遍历的迭代法思路不能直接套用到中序遍历上。
在迭代的过程中有两个操作:
1、【处理】将元素放入result数组
2、【访问】遍历结点
前序遍历中：遍历的顺序是中左右。
先访问中间结点，先处理中间结点
要访问的元素和要处理的元素的顺序一致，都是中间结点。
而中序遍历，遍历顺序为左中右。
先访问二叉树顶部结点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理结点（再把结点的数值放到result数组中）；
这就导致了处理顺序和访问顺序不一致
所以在使用迭代 法时，需要借用指针的遍历来帮助访问结点，使用栈来处理结点上的元素。
在这里插入图片描述

class Solution{
public:vector<int> inorderTraversal(TreeNode* root){vector<int> result;stack<TreeNode*> st;TreeNode* cur = root;while(!st.empty() || cur!=NULL){if(cur!=NULL){st.push(cur);cur = cur->left;    //先一直都是从左结点深入，直到某一个结点的左孩子为NULL}//如果该点是父结点的左孩子，且指向空，则将cur指向它的父结点（为最深的左结点），然后将父结点出栈，将值赋给结果数组，再将指针指向此父结点的右孩子（这样保证了左中右的遍历顺序）else{cur = st.top();st.pop();result.push_back(cur->val);cur = cur->right;}          }return result;}
};

3、后序遍历（迭代法）

后序遍历：左右中。
先序遍历：中左右。
我们只需要调整一下先序遍历的代码顺序，变为中右左的遍历顺序。
然后反转result数组，输出结果就是左右中。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> st;		//构建一个栈vector<int> result;st.push(root);			//先将根结点压入栈中while(!st.empty()){			//当栈中还有元素时TreeNode* node = st.top();	//将栈顶元素赋给新结点	st.pop();					//将栈顶元素出栈if(node !=NULL) result.push_back(node->val);	//如果这个结点不为空，将值赋给resultelse continue;									//否则继续，（也就是说如果结点为空不赋值）st.push(node->left);		//将该中结点的左孩子压入栈中st.push(node->right);		//将该结点中的右孩子压入栈中}//反转resultreverse(result.begin(),result.end());return result;}
};

4、二叉树深度优先遍历迭代算法格式统一

之前迭代法例子中提到无法同时解决访问节点（遍历）和处理结点（将结点放入结果）不一致的情况。
解决方法：
将访问的结点放入栈中，把要处理的结点也放入栈中，但是要做标记
标记方法：将要处理的结点放入栈中之后，紧接着放入一个空指针作为标记
将访问的结点直接加入到栈中，但是如果是处理的结点则后面放入一个空结点，这样只有空结点弹出的时候才将下一个结点放进结果集。
如何知道该访问的结点是我们需要处理的结点？（中结点是我们需要处理的结点），所以只需要在中结点后面加入一个空结点就行了
中序遍历：

class Solution{
public:vector<int> inorderTraversal(TreeNode* root){vector<int> result;stack<TreeNode*> st;if(root !=NULL) st.push(root);while(!st.empty()){TreeNode* node = st.top();  //标记操作，直到遇到NULLif(node!=NULL){//将该结点弹出，避免重复操作st.pop();//添加右结点if(node->right) st.push(node->right);//添加中结点st.push(node);//标记st.push(NULL); //添加左结点if(node->left) st.push(node->left);}//只有遇到空结点的时候，才将下一个结点放入到结果中else{//弹出空结点st.pop();node = st.top();st.pop();   result.push_back(node->val);}}return result;}
};

先序遍历：中左右

class Solution{
public:vector<int> preorderTraversal(TreeNode* root){vector<int> result;stack<TreeNode*> st;if(root !=NULL) st.push(root);while(!st.empty()){TreeNode* node = st.top();  //标记操作，直到遇到NULLif(node!=NULL){//将该结点弹出，避免重复操作st.pop();//添加右结点if(node->right) st.push(node->right);//添加左结点if(node->left) st.push(node->left);//添加中结点st.push(node);//标记st.push(NULL); }//只有遇到空结点的时候，才将下一个结点放入到结果中else{//弹出空结点st.pop();node = st.top();st.pop();   result.push_back(node->val);}}return result;}
};

后序遍历：左右中

class Solution{
public:vector<int> postorderTraversal(TreeNode* root){vector<int> result;stack<TreeNode*> st;if(root !=NULL) st.push(root);while(!st.empty()){TreeNode* node = st.top();  //标记操作，直到遇到NULLif(node!=NULL){//将该结点弹出，避免重复操作st.pop();//添加中结点st.push(node);//标记st.push(NULL); //添加右结点if(node->right) st.push(node->right);//添加左结点if(node->left) st.push(node->left);}//只有遇到空结点的时候，才将下一个结点放入到结果中else{//弹出空结点st.pop();node = st.top();st.pop();   result.push_back(node->val);}}return result;}
};

总结：

这种方法比较好记忆，主要注意以下几点
1、栈的特性入栈和出栈相反，所以如果想输出顺序为“左中右”，入栈顺序必须为“右中左”
2、入栈的处理：可以将整个树简化为3个结点一组的多个子树。每次循环处理的实际就是将这样的3个结点按照规定的顺序进行入栈。
3、NULL结点的加入以及出栈规则的指定：
以中序遍历为例，保证了当左孩子作为栈顶元素时不会立即出栈，而是会将当前的左孩子(栈顶元素)作为下次遍历的父结点；接着按照规则顺序入栈，直到当前的左孩子作为父结点再无孩子时（此时是入栈规则为父结点、NULL结点），遇到NULL结点，进行出栈。

5、二叉树层序遍历

1、leetcode102:二叉树的层序遍历

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。
示例：
二叉树：[3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回其层次遍历结果：

[
[3],
[9,20],
[15,7]
]
思考：
借用队列来实现，【队列先进先出，符合一层一层遍历的逻辑】
而栈先进后出适合模拟深度优先遍历也就是递归地逻辑。
【这种层序遍历的方式就是图论中的广度优先遍历，只不过用在了二叉树上】
思考：
在这里插入图片描述

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> que;if(root!=NULL) que.push(root);vector<vector<int>> result;while(!que.empty()){//该层结点元素个数 = 该层队列元素int size = que.size();vector<int> vec;//这里要使用固定大小的size，不能使用que.size(),因为在处理中que.size是不断变化的//将这层元素送入队列中并依次从队首向队尾将元素出队列，每个元素出队列的同时又将其不为空的子结点送入队列for(int i =0;i<size;i++){TreeNode* node = que.front();//将队首元素送入该层结果que.pop();vec.push_back(node->val);//将左右孩子结点入队列，作为下一层的元素if(node->left) que.push(node->left);if(node->right) que.push(node->right);}result.push_back(vec);}return result;}
};

2、leetcode107:二叉树的层序遍历 II

给定一个二叉树，返回其节点值自底向上的层次遍历。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）
例如：
给定二叉树 [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回其自底向上的层次遍历为：

[
[15,7],
[9,20],
[3]
]
思路：在层序遍历的基础上进行直接反转

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {queue<TreeNode*> que;if(root!=NULL) que.push(root);vector<vector<int>> result;while(!que.empty()){//该层结点元素个数 = 该层队列元素int size = que.size();vector<int> vec;//这里要使用固定大小的size，不能使用que.size(),因为在处理中que.size是不断变化的//将这层元素送入队列中并依次从队首向队尾将元素出队列，每个元素出队列的同时又将其不为空的子结点送入队列for(int i =0;i<size;i++){TreeNode* node = que.front();//将队首元素送入该层结果que.pop();vec.push_back(node->val);//将左右孩子结点入队列，作为下一层的元素if(node->left) que.push(node->left);if(node->right) que.push(node->right);}result.push_back(vec);}//将层序遍历反转一下结果reverse(result.begin(),result.end());return result;}
};

3、leetcode199:二叉树的右视图

给定一棵二叉树，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。
示例:
输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:
1 <—
/
2 3 <—
\
5 4 <—
思路：对层序遍历的的结果的每个子层result取最后的一个，作为结果返回。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:vector<int> rightSideView(TreeNode* root) {queue<TreeNode*> que;if(root!=NULL) que.push(root);vector<int> realresult;while(!que.empty()){//该层结点元素个数 = 该层队列元素int size = que.size();vector<int> vec;//这里要使用固定大小的size，不能使用que.size(),因为在处理中que.size是不断变化的//将这层元素送入队列中并依次从队首向队尾将元素出队列，每个元素出队列的同时又将其不为空的子结点送入队列for(int i =0;i<size;i++){TreeNode* node = que.front();//将队首元素送入该层结果que.pop();vec.push_back(node->val);//将左右孩子结点入队列，作为下一层的元素if(node->left) que.push(node->left);if(node->right) que.push(node->right);}realresult.push_back(vec[size-1]);}return realresult;}
};

4、leetcode637:二叉树的层平均值

给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。
示例 1：
输入：
3
/
9 20
/
15 7
输出：[3, 14.5, 11]
解释：
第 0 层的平均值是 3 , 第1层是 14.5 , 第2层是 11 。因此返回 [3, 14.5, 11] 。
提示：
节点值的范围在32位有符号整数范围内。

思考：层序遍历中加入累加以及求均值操作

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:vector<double> averageOfLevels(TreeNode* root) {queue<TreeNode*> que;if(root!=NULL) que.push(root);vector<double> realresult;while(!que.empty()){//该层结点元素个数 = 该层队列元素int size = que.size();vector<int> vec;double sum = 0;//这里要使用固定大小的size，不能使用que.size(),因为在处理中que.size是不断变化的//将这层元素送入队列中并依次从队首向队尾将元素出队列，每个元素出队列的同时又将其不为空的子结点送入队列for(int i =0;i<size;i++){TreeNode* node = que.front();//将队首元素送入该层结果que.pop();vec.push_back(node->val);sum+=vec[i];//将左右孩子结点入队列，作为下一层的元素if(node->left) que.push(node->left);if(node->right) que.push(node->right);}realresult.push_back(sum /size);}return realresult;}
};

5、leetcode429:N叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。 (即从左到右，逐层遍历)。
例如，给定一个 3叉树 :
返回其层序遍历:
[
[1],
[3,2,4],
[5,6]
]
说明:
树的深度不会超过 1000。
树的节点总数不会超过 5000。
思考：与二叉树层序遍历方法一样，不过子结点的个数不定

/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
public:vector<vector<int>> levelOrder(Node* root) {queue<Node*> que;if(root!=NULL) que.push(root);vector<vector<int>> result;while(!que.empty()){//该层结点元素个数 = 该层队列元素int size = que.size();vector<int> vec;//这里要使用固定大小的size，不能使用que.size(),因为在处理中que.size是不断变化的//将这层元素送入队列中并依次从队首向队尾将元素出队列，每个元素出队列的同时又将其不为空的子结点送入队列for(int i =0;i<size;i++){Node* node = que.front();//将队首元素送入该层结果que.pop();vec.push_back(node->val);//将所有孩子结点入队列，作为下一层的元素for(int j=0;j<node->children.size();j++){if(node->children[j]) que.push(node->children[j]);}}result.push_back(vec);}return result;}
};

6、leetcode515. 在每个树行中找最大值

您需要在二叉树的每一行中找到最大的值。
示例：
输入:
1
/
3 2
/ \ \
5 3 9

输出: [1, 3, 9]
思考：层序遍历，然后在每层中找最大值

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> largestValues(TreeNode* root) {queue<TreeNode*> que;if(root!=NULL) que.push(root);vector<int> result;while(!que.empty()){//该层结点元素个数 = 该层队列元素int size = que.size();int max=-2147483648;    //(最小值)vector<int> vec;//这里要使用固定大小的size，不能使用que.size(),因为在处理中que.size是不断变化的//将这层元素送入队列中并依次从队首向队尾将元素出队列，每个元素出队列的同时又将其不为空的子结点送入队列for(int i =0;i<size;i++){TreeNode* node = que.front();//将队首元素送入该层结果que.pop();vec.push_back(node->val);if(max<=node->val) max = node->val;//将左右孩子结点入队列，作为下一层的元素if(node->left) que.push(node->left);if(node->right) que.push(node->right);}result.push_back(max);}return result;}
};

7、leetcode116. 填充每个节点的下一个右侧节点指针

给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。
初始状态下，所有 next 指针都被设置为 NULL。

示例：
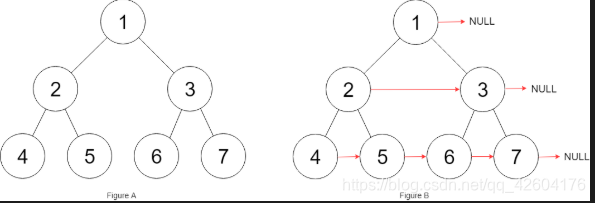
在这里插入图片描述
在这里插入图片描述
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。
提示：
你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

思考：层序遍历，只不过在单层遍历的时候记录本层的头部节点，然后在遍历的时候让前一个节点指向本节点。

/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
public:Node* connect(Node* root) {queue<Node*> que;if(root!=NULL) que.push(root);while(!que.empty()){int size = que.size();Node* node;Node* Prenode;for(int i =0;i<size;i++){//每层第一个元素元素if(i==0){Prenode =que.front();que.pop();node = Prenode;}//非每层第一个结点else{node = que.front();que.pop();//将此结点与上一个结点连在一起Prenode->next = node;Prenode = node; }//将左右孩子结点入队列，作为下一层的元素if(node->left) que.push(node->left);if(node->right) que.push(node->right);}Prenode->next =NULL;}return root;}
};

8、leetcode117. 填充每个节点的下一个右侧节点指针 II（遇上一题思路代码一致）

给定一个二叉树
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。
初始状态下，所有 next 指针都被设置为 NULL。

进阶：
你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。
在这里插入图片描述

9、104. 二叉树的最大深度

思路：层序遍历，每层对一个变量++即可
给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

3

/
9 20
/
15 7
返回它的最大深度 3 。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:int maxDepth(TreeNode* root) {queue<TreeNode*> que;if(root!=NULL) que.push(root);int result=0;while(!que.empty()){//该层结点元素个数 = 该层队列元素int size = que.size();//这里要使用固定大小的size，不能使用que.size(),因为在处理中que.size是不断变化的//将这层元素送入队列中并依次从队首向队尾将元素出队列，每个元素出队列的同时又将其不为空的子结点送入队列for(int i =0;i<size;i++){TreeNode* node = que.front();//将队首元素送入该层结果que.pop();//将左右孩子结点入队列，作为下一层的元素if(node->left) que.push(node->left);if(node->right) que.push(node->right);}result++;}return result; }
};

10、111. 二叉树的最大深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

示例:

给定二叉树 [3,9,20,null,null,15,7],

3

/
9 20
/
15 7
返回它的最小深度 2.
思考：层序遍历，若当前层有一个结点的左孩子和右孩子均无则可以确定最小深度。
不过这个思路的效率很低

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int minDepth(TreeNode* root) {queue<TreeNode*> que;if(root!=NULL) que.push(root);int result=0;int break_flag=0;while(!que.empty()){//该层结点元素个数 = 该层队列元素int size = que.size();//这里要使用固定大小的size，不能使用que.size(),因为在处理中que.size是不断变化的//将这层元素送入队列中并依次从队首向队尾将元素出队列，每个元素出队列的同时又将其不为空的子结点送入队列for(int i =0;i<size;i++){TreeNode* node = que.front();//将队首元素送入该层结果que.pop();if(!node->left && !node->right){return result+1;} //将左右孩子结点入队列，作为下一层的元素if(node->left) que.push(node->left);if(node->right) que.push(node->right);}result++;}return result;  }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/378051.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

ZZ的计算器

ZZ的计算器

Problem Description ZZ自从上大学以来&#xff0c;脑容量就是以SB计算的&#xff0c;这个吃货竟然连算术运算也不会了&#xff0c;可是当今的计算机可是非常强大的&#xff0c;作为ACMer&#xff0c; 几个简单的算术又算得了什么呢&#xff1f;可是该怎么做呢&#xff1f;ZZ只…
阅读更多...
kotlin 覆盖属性_Kotlin程序| 方法覆盖的示例

kotlin 覆盖属性_Kotlin程序| 方法覆盖的示例

kotlin 覆盖属性方法重载 (Method Overriding) Method overriding allows derived class has the same function name and signature as the base class 方法重写允许派生类具有与基类相同的函数名称和签名 By method overriding we can provide different implementation into…
阅读更多...
对视频中的特征颜色物体(青色水杯)进行跟踪

对视频中的特征颜色物体(青色水杯)进行跟踪

方法一&#xff1a;目标物体白色&#xff0c;其余黑色 import cv2 import numpy as npdef extrace_object():capture cv2.VideoCapture("G:/Juptyer_workspace/study/data/yy.mp4")while(True):ret,frame capture.read()if retFalse:breakhsv cv2.cvtColor(frame…
阅读更多...
Android实现号码归属地查询

Android实现号码归属地查询

我们通过发送XML访问 WebService就可以实现号码的归属地查询&#xff0c;我们可以使用代理服务器提供的XML的格式进行设置&#xff0c;然后请求提交给服务器&#xff0c;服务器根据请求就会返回给一个XML&#xff0c;XML中就封装了我们想要获取的数据。 发送XML 1.通过URL封装路…
阅读更多...
如何从 Datagrid 中获得单元格的内容与 使用值转换器进行绑定数据的转换IValueConverter...

如何从 Datagrid 中获得单元格的内容与 使用值转换器进行绑定数据的转换IValueConverter...

一、如何从 Datagrid 中获得单元格的内容 DataGrid 属于一种 ItemsControl, 因此&#xff0c;它有 Items 属性并且用ItemContainer 封装它的 items. 但是&#xff0c;WPF中的DataGrid 不同于Windows Forms中的 DataGridView。 在DataGrid的Items集合中&#xff0c;DataGridRow…
阅读更多...
【C++ grammar】常量、指针、Usage of using, typedef, and #define

【C++ grammar】常量、指针、Usage of using, typedef, and #define

目录1、常量 &#xff08;Constant&#xff09;2、指针&#xff08;Pointer&#xff09;3、Usage of using, typedef, and #define1、常量 &#xff08;Constant&#xff09; 常量是程序中一块数据&#xff0c;这个数据一旦声明后就不能被修改了。 如果这块数据有一个名字&am…
阅读更多...
斯威夫特山地车_斯威夫特| 两个数字相加的程序

斯威夫特山地车_斯威夫特| 两个数字相加的程序

斯威夫特山地车In this program, we will have an idea - how two numbers can be added and displayed as the output on the screen? 在此程序中&#xff0c;我们将有一个想法- 如何将两个数字相加并显示为屏幕上的输出 &#xff1f; Open XCode terminal and type the fol…
阅读更多...
四、色彩空间

四、色彩空间

一、色彩空间 1、什么是色彩空间&#xff1f; 色彩空间是定义的颜色范围。 2、常见的色彩空间有哪些&#xff1f; ①RGB ②HSV 在OpenCV中&#xff0c;Hue的值为0~180&#xff0c;之所以不是360是因为&#xff0c;8位存不下&#xff0c;故进行归一化操作&#xff0c;使得H…
阅读更多...
Oracle LOB 详解

Oracle LOB 详解

一. 官方说明Oracle 11gR2 文档&#xff1a;LOB Storagehttp://download.oracle.com/docs/cd/E11882_01/appdev.112/e18294/adlob_tables.htm#ADLOB45267Oracle 10gR2 文档&#xff1a;LOBs in Tableshttp://download.oracle.com/docs/cd/B19306_01/appdev.102/b14249/adlob_t…
阅读更多...
FIFA的完整形式是什么？

FIFA的完整形式是什么？

国际足联&#xff1a;国际足球联合会 (FIFA: Federation Internationale de Football Association) FIFA is an abbreviation of the "Federation Internationale de Football Association" in French. It is also known as the International Federation of Associa…
阅读更多...
POJ 1654 Area

POJ 1654 Area

题意&#xff1a;从原点出发&#xff0c;沿着8个方向走&#xff0c;每次走1个点格或者根号2个点格的距离&#xff0c;最终回到原点&#xff0c;求围住的多边形面积。分析&#xff1a;直接记录所经过的点&#xff0c;然后计算多边形面积。注意&#xff0c;不用先保存所有的点&am…
阅读更多...
【C++ grammar】重载、内联、变量作用域、带默认参数的函数

【C++ grammar】重载、内联、变量作用域、带默认参数的函数

目录1、变量的作用域1. 变量的作用域分类2. Unary Scope Resolution (一元作用域解析运算符)2、重载函数3、带有默认参数值的函数4、重载函数 VS 带有默认参数值的函数5、内联函数&#xff08;Inline Function&#xff09;1. 普通函数的优缺点2. 使用内联函数3. 定义内联函数4.…
阅读更多...
五、像素运算

五、像素运算

一、相关概念 1、算术运算 Ⅰ加减乘除 Ⅱ调节亮度 Ⅲ调整对比度 2、逻辑运算 Ⅰ与或非 Ⅱ遮罩层控制 二、图像算术运算(加减乘除均值方差) 其中图像的加减乘除需要保证两张图像的大小相同 import cv2 import numpy as npdef add(src1,src2):dst cv2.add(src1,src2)cv2.im…
阅读更多...
创建bootstrap项目_使用Bootstrap创建第一个网页

创建bootstrap项目_使用Bootstrap创建第一个网页

创建bootstrap项目使用Bootstrap创建第一个网页 (Create First Webpage with Bootstrap) In the previous article, we learned "how to setup bootstrap?" for a web project. If you haven’t gone through that, it is recommended to read it. Now, in this art…
阅读更多...
Chaikin Curve(球面插值)

Chaikin Curve(球面插值)

在两条折线间完成平滑的过渡是 用画布做UI 或者做类似地图编辑器一类的工作的 很常见的任务。 怎么样化方为圆是决定工作效率的很重要的因素。&#xff08;当需要编辑的曲线多起来&#xff0c; 复杂起来的时候&#xff0c;这会是件相当繁重的工作&#xff09; 最容易想到的莫非…
阅读更多...
【2020 电设G题 图像题解】

【2020 电设G题 图像题解】

博主联系方式： QQ:1540984562 QQ交流群：892023501 群里会有往届的smarters和电赛选手，群里也会不时分享一些有用的资料，有问题可以在群里多问问。 2022.3.10新增订阅通知 近期把此专栏设置为了付费模式，可以直接花9.9买这个专栏，买了就可以直接这个专栏的所有文章了。后…
阅读更多...
六、ROI和泛洪填充

六、ROI和泛洪填充

一、ROI ROI&#xff1a;region of interest&#xff0c;即感兴趣区域。 一般主要通过numpy来获取ROI 将某区域转变为灰色图片再覆盖原图像 import cv2 import numpy as npsrc cv2.imread(r"G:\Juptyer_workspace\study\opencv\opencv3\a1.jpg") cv2.imshow(&quo…
阅读更多...
VS2005 there is no source code available for the current location 解决方案

VS2005 there is no source code available for the current location 解决方案

1.首先试最常规的方法&#xff1a;Clean and then rebuild solution&#xff0c;但是没有解决 2.进入Tools>Options,选择Debugging>General 却掉 Enable address-level debugging 选项&#xff0c;在去掉 Require source files to exactly match the original version. O…
阅读更多...
django 静态数据_如何在Django中使用静态数据？

django 静态数据_如何在Django中使用静态数据？

django 静态数据Static Data means those data items that we cannot want to change, we want to use them as it is like audio, video, images, files etc. 静态数据是指我们不想更改的数据项&#xff0c;我们想像音频&#xff0c;视频&#xff0c;图像&#xff0c;文件等那…
阅读更多...
Leetcode226. 翻转二叉树(递归、迭代、层序三种解法)

Leetcode226. 翻转二叉树(递归、迭代、层序三种解法)

目录题目1、层序法&#xff1a;2、递归法&#xff1a;1、先序遍历&#xff08;中左右&#xff09;2、后序遍历&#xff08;左右中&#xff09;3、递归中序遍历为什么不行&#xff08;左中右&#xff09;3、迭代法&#xff1a;1、先序遍历2、中序遍历3、后序遍历为什么迭代法的中…
阅读更多...
最新文章

Copyright @ 2022~2023