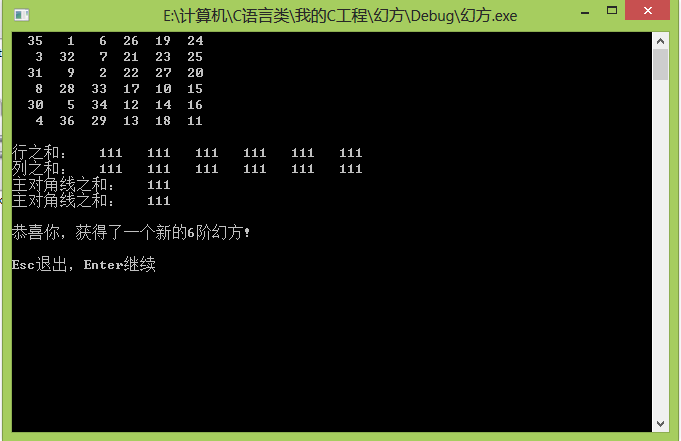
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <windows.h> 4 5 #define EVEN_DOUBLE_4 4 //双偶的最基本类型,4阶双偶 6 #define SCREEN_SIZE 19 //屏幕显示不变形的最大尺寸(主要是因为窗口大小限制) 7 #define MIN_SIZE 3 //最小阶数为3 8 #define MAX_SIZE 30 9 /*原则上是任意阶,算法是相同的,这里就以30为上限吧, 10 当然如果你愿意,可以修改的更大一些*/ 11 12 #define PRINT printf("Esc退出,Enter继续"); //打印的宏 13 #define CLEAR row = 0; column = 0; //清零 14 15 int Magic[MAX_SIZE][MAX_SIZE]={0}; //全局,幻方数组 16 int row = 0; column = 0; //全局,幻方的行列数 17 18 19 int main(void) 20 { 21 int read(); //读取函数 22 void odd(int size, int ini_value ); //奇数阶幻方生成 23 void mean_double_4(int size); //4阶双偶生成 24 void mean_double(int size); //双偶生成 25 void mean_single(int size); //单偶生成 26 void print_magic(int size); //打印幻方 27 void sum_print(int data[], int size); //行、列、对之和打印 28 void clear_sum(int data[]); 29 void check_magic(int data[], int size ); //检查所得矩阵是否为幻方阵 30 31 int size; //幻方阶数 32 int sum[2*MAX_SIZE+2] = {0};//行、列、对之和 33 34 do{ 35 CLEAR 36 clear_sum(sum); 37 size=read(); 38 system("cls"); 39 40 if(size%2 != 0 ) odd(size, 0); 41 else if(size %4 == 0) mean_double(size); 42 else mean_single(size); 43 44 print_magic(size); 45 sum_print(sum, size); 46 check_magic(sum,size); 47 PRINT 48 49 }while (getch() != 27); 50 51 return 0; 52 } 53 54 /*读入数据*/ 55 int read() 56 { 57 int min_size = MIN_SIZE; 58 int max_size = MAX_SIZE; 59 int size; 60 61 do{ 62 printf("请输入幻方阶数n,n∈[%d,%d]\n", min_size, max_size); 63 scanf("%d", &size); 64 getchar(); 65 if(size<3 || size > MAX_SIZE) printf("非法输入,请重新输入[%d,%d]的正整数\n", min_size, max_size); 66 else if(size > SCREEN_SIZE){ 67 printf("大于屏显最大阶数,输出将变形\n"); 68 Sleep(2000); 69 } 70 }while(size < MIN_SIZE || size > MAX_SIZE); 71 72 return size; 73 } 74 75 76 /*奇数阶幻方,采用house法*/ 77 void odd(int size, int ini_value) 78 { 79 int num; //填充数字 80 int min_num = 1+ini_value; 81 int max_num = 1+size*size+ini_value; //填充范围 82 int x = size/2; 83 int y = 0; //初始填充坐标 84 85 for(num = min_num; num < max_num; num++){ 86 Magic[y+row][x+column] = num; 87 if(num % size == 0) y++; //跳步 88 else x++, y += 2; //马步,其实Horse法和Siamese是完全类似的 89 x = x % size ; 90 y = y % size ; 91 /*越界反弹,即触碰到边界,从另一边返回*/ 92 } 93 } 94 95 /*双偶数阶幻方,采用对调法*/ 96 97 /*对调法的基础,4阶双偶。注意要求是将非主副对角线上的元素对调, 98 其实换个角度,你也可以说就是把祝福对角线中心对调。只不过两种思路得到的矩阵 99 正好是反着来的*/ 100 /*本函数实现主副对角线互调*/ 101 void mean_double_4(int size) 102 { 103 104 int i; 105 int total = size * size +1 ; 106 for(i = 0; i < EVEN_DOUBLE_4; i++){ 107 Magic[row+i][column+i] = total - Magic[row+i][column+i]; 108 Magic[row+i][ EVEN_DOUBLE_4+column-i-1] = 109 total - Magic[row+i][ EVEN_DOUBLE_4+column-i-1]; 110 } 111 112 } 113 114 /*任意阶双偶*/ 115 void mean_double(int size) 116 { 117 int num; //填充数字 118 int min_num = 1; 119 int max_num = 1+size*size; //填充范围 120 int i = 0; //循环变量 121 int temp; 122 123 /*双偶,初始化*/ 124 for(num = min_num; num < max_num; num++){ 125 Magic[row][column] = num; 126 if((num ) % (size ) == 0){ 127 column = 0, row++; 128 } 129 else column++; 130 } 131 132 133 /*分割为4×4的小矩阵*/ 134 row = 0; column = 0; 135 temp = size / EVEN_DOUBLE_4; 136 137 for(i = 1; i <=temp *temp; i++){ 138 mean_double_4(size); 139 if(i % temp == 0) column = 0, row += 4 ; 140 else column = (i % temp) * EVEN_DOUBLE_4; 141 } 142 } 143 144 145 /*单偶,用楼梯法*/ 146 void mean_single(int size) 147 { 148 int i,j,k,m; 149 int temp; 150 151 152 /*分象限处理, 153 14 154 32 155 与普通直角坐标系象限区别,说白了,就是个分块的概念 156 */ 157 row = 0, column = 0; //第一象限 158 odd(size/2, 0); 159 160 row = size/2, column = size/2; //第二象限 161 odd(size/2, (size*size)/4*1); 162 163 row = 0, column = size/2; //第三象限 164 odd(size/2, (size*size)/4*2); 165 166 167 row = size/2, column = 0; //第四象限 168 odd(size/2, (size*size)/4*3); 169 170 m = size / 4; 171 172 /*对换*/ 173 for(i = 0; i< size/2; i++){ 174 /*1、3象限对换*/ 175 for(j = 0; j<m; j++ ){ 176 if(i == m) k = j + m; 177 else k = j; 178 temp = Magic[i][k]; 179 Magic[i][k] = Magic[i + 2*size/4 ][k]; 180 Magic[i + 2*size/4 ][k] = temp; 181 } 182 /*2,4对换*/ 183 for(j = 0; j<m-1; j++ ){ 184 k = 3*size/4 +j; 185 temp = Magic[i][k]; 186 Magic[i][k] = Magic[i + 2*size/4][k]; 187 Magic[i + 2*size/4][k] = temp; 188 } 189 } 190 } 191 192 /*打印幻方*/ 193 void print_magic(int size) 194 { 195 int i,j; 196 for(i = 0; i < size; i++) 197 for(j = 0; j < size; j++){ 198 printf("%4d", Magic[i][j]); 199 if(j == size -1) putchar('\n'); 200 } 201 putchar('\n'); 202 } 203 204 /*打印各行、各列、各对角线数据之和*/ 205 void sum_print(int data[], int size) 206 { 207 int i,j; 208 209 /*打印每行数据之和*/ 210 printf("行之和:"); 211 for(i = 0; i < size; i++) 212 for(j = 0; j < size; j++){ 213 data[i] += Magic[i][j]; //行之和 214 if (j == size -1) printf("%6d", data[i]); 215 } 216 putchar('\n'); 217 218 219 /*打印每列数据之和*/ 220 printf("列之和:"); 221 for(i = 0; i < size; i++) 222 for(j = 0; j < size; j++){ 223 data[size+i] += Magic[j][i]; //列之和 224 if (j == size -1) printf("%6d", data[size+i]); 225 } 226 putchar('\n'); 227 228 229 /*打印主对角线之和*/ 230 for(i=0; i<size; i++) 231 data[2*size] += Magic[i][i]; 232 printf("主对角线之和:%6d", data[2*size]); 233 putchar('\n'); 234 235 /*打印副对角线之和*/ 236 for(i=0; i<size; i++) 237 data[2*size+1] += Magic[i][size-i-1]; 238 printf("主对角线之和:%6d", data[2*size]); 239 putchar('\n'); 240 241 } 242 243 /*行列对和数组清零*/ 244 void clear_sum(int data[]) 245 { 246 int i; 247 for(i = 0; i < 2 * MAX_SIZE; i++) 248 data[i] = 0; 249 } 250 251 /*检查程序是否运转正常,所得结果是否是幻方*/ 252 void check_magic(int data[], int size ) 253 { 254 int i; 255 int flag = 0; 256 for(i=1; i<size+2;i++) 257 if(data[0]-data[i]) flag = 1; 258 if(flag) printf("程序出错,Esc退出,Enter继续\n"); 259 else printf("\n恭喜你,获得了一个新的%d阶幻方!\n", size); 260 putchar('\n'); 261 262 }

Service Mesh)

Database Replication)
)
Database Partitioning)

Database Denormalization)


NoSQL)
)
缓存)
![[linux]gdb调试](http://pic.xiahunao.cn/[linux]gdb调试)
异步机制与MQ)



)
