EM, ExpectationMaximization Algorithm, 期望最大化算法。一种迭代算法,用于含有隐变量(hidden variable)的概率参数模型的最大似然估计或极大后验概率估计,其概率模型依赖于无法观测的隐变量。
经常用在ML与计算机视觉的数据聚类领域。
EM应用:GMM混合高斯模型、聚类、HMM隐马尔科夫模型等。
一、Jesen不等式
对于凸函数(对于所有实数x,有f’’(x)≥0)。当x时向量时,如果其hessian矩阵H是半正定的(H≥0),那么f是凸函数。如果f’’(x)>0或者H>0,那么f是严格凸函数。
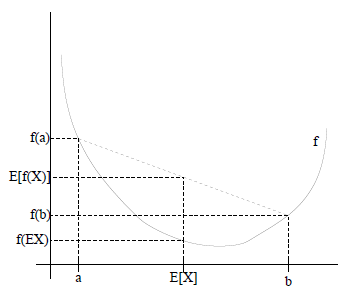
关于Jesen不等式:如果f是凸函数,x是随机变量,那么有
E[f(x)]≥ f(Ex)
图形化的表示方法就是:
二、EM原理
最大期望个算法经过两个步骤交替进行计算
step1: 计算期望E,利用对隐藏变量的现有估计值,计算其最大似然估计值。
step2: 最大化M,最大化在E步上求得的最大似然值来计算参数值。
(M步上找到的参数估计值被用于下一个E步计算中,这个过程不断交替进行)
三、EM算法流程
1. 初始化分布参数
2. 重复直到收敛:
E步骤:估计位置参数的期望值,给出当前的参数估计
M步骤:重新估计分布参数,以使得数据似然性最大,给出位置变量的期望估计。
EM是一种解决存在隐含变量优化问题的有效方法,既然不能直接最大化L(o),可以不断建立l的下界(E步),然后优化下界(M步)。