[BZOJ3529][Sdoi2014]数表
试题描述
有一张N×m的数表，其第i行第j列（1 < =i < =n，1 < =j < =m）的数值为能同时整除i和j的所有自然数之和。给定a，计算数表中不大于a的数之和。
输入
输入包含多组数据。
输入的第一行一个整数Q表示测试点内的数据组数，接下来Q行，每行三个整数n，m，a(|a| < =10^9)描述一组数据。
输入的第一行一个整数Q表示测试点内的数据组数，接下来Q行，每行三个整数n，m，a(|a| < =10^9)描述一组数据。
输出
对每组数据，输出一行一个整数，表示答案模2^31的值。
输入示例
2 4 4 3 10 10 5
输出示例
20 148
数据规模及约定
1 < =N．m < =10^5 ， 1 < =Q < =2×10^4
题解
我们设 f(i) 表示 i 的所有约数和，g(i) 表示 x∈[1, n]，y∈[1, m] 范围内有多少对 (x, y) 使得 gcd(x, y) = i。
那么 f(i) 可以线性筛求出，g(i) 可以莫比乌斯反演得出。
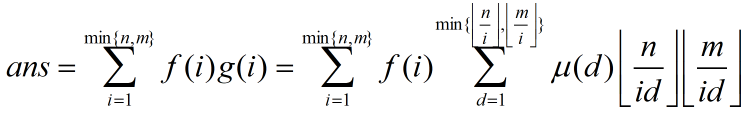
令 T = id，并交换求和顺序，得到
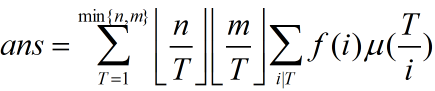
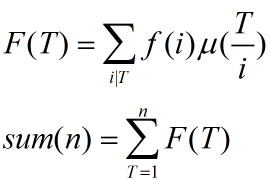
受到前面题的启发，我们可以用调和级数的复杂度求得所有的 F(T)。
那么现在还要求 f(i) ≤ a，咋办？
离线，把询问按照 a 的大小排序，按照 f(i) 的大小顺序依次插入，每次更新 F(T)，然后树状数组更新 sum(n)。
查询的时候，按照 [n / T][m / T] 分类计算，总复杂度 O(n log2n + n sqrt(n) logn)。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {if(Head == Tail) {int l = fread(buffer, 1, BufferSize, stdin);Tail = (Head = buffer) + l;}return *Head++;
}
int read() {int x = 0, f = 1; char c = Getchar();while(!isdigit(c)){ if(c == '-') f = -1; c = Getchar(); }while(isdigit(c)){ x = x * 10 + c - '0'; c = Getchar(); }return x * f;
}#define maxn 100010const int MOD = 2147483647;
int prime[maxn], cp, mu[maxn], smu[maxn], remain[maxn], f[maxn], Ord[maxn];
bool vis[maxn];
bool cmp(int a, int b) { return f[a] < f[b]; }
void init() {mu[1] = 1; f[1] = 1;for(int i = 2; i < maxn; i++) {if(!vis[i]) prime[++cp] = i, mu[i] = -1, f[i] = 1 + i, remain[i] = 1;for(int j = 1; i * prime[j] < maxn && j <= cp; j++) {vis[i*prime[j]] = 1;if(i % prime[j] == 0) {mu[i*prime[j]] = 0;f[i*prime[j]] = f[i] + f[remain[i]] * (i / remain[i] * prime[j]);remain[i*prime[j]] = remain[i];break;}mu[i*prime[j]] = -mu[i];f[i*prime[j]] = f[i] * (prime[j] + 1);remain[i*prime[j]] = i;}smu[i] = smu[i-1] + mu[i];}for(int i = 1; i < maxn; i++) Ord[i] = i;sort(Ord + 1, Ord + maxn, cmp);return ;
}struct Que {int n, m, a, id;Que() {}Que(int _1, int _2, int _3, int _4): n(_1), m(_2), a(_3), id(_4) {}bool operator < (const Que& t) const { return a < t.a; }
} qs[maxn];
int Ans[maxn];int S[maxn];
void Add(int x, int v) {for(; x < maxn; x += x & -x) S[x] += v;return ;
}
int Sum(int x) {int ans = 0;for(; x; x -= x & -x) ans += S[x];return ans;
}int main() {init();int T = read();for(int i = 1; i <= T; i++) {int n = read(), m = read(), a = read();qs[i] = Que(n, m, a, i);}sort(qs + 1, qs + T + 1);int j = 1;for(int q = 1; q <= T; q++) {while(j < maxn && f[Ord[j]] <= qs[q].a) {for(int d = 1; Ord[j] * d < maxn; d++) Add(Ord[j] * d, f[Ord[j]] * mu[d]);j++;}int n = qs[q].n, m = qs[q].m; if(n > m) swap(n, m);for(int i = 1, lst; i <= n; i = lst + 1) {lst = min(n / (n / i), m / (m / i));Ans[qs[q].id] += (n / i) * (m / i) * (Sum(lst) - Sum(i - 1));}}for(int i = 1; i <= T; i++) printf("%d\n", Ans[i] & MOD);return 0;
}
