今天再次迎来了我们的例行考试。
T1:


首先我们考虑那些点是可以共存的,我们可以枚举一个质数做他们的gcd,然后把这些点放在一张图里求直径。
所以我们要做的就是把这些点的值分解质因数,对每个质因数挂一个链,代表有那些点包含这些质因数。然后我们枚举质因数,把这条链上的点放进图里求直径即可。由于质因数最多log个,所以复杂度nlogn。
然而分解质因数怎么做呢?10w个数,1e9的范围,暴力sqrt的分解肯定过不去,我们需要pollard rho。
然而考场上我想:pollard rho可能被卡(我才不告诉你我不会写pollard rho呢),暴力分解又过不去。况且暴力分解在最差情况下连5000都过不去,我还不如敲个n^2log的暴力呢,然后就敲了一个裸暴力进去。
结果正解就是sqrt的暴力分解,很多人都这样A了。也就是说,我们1e10的计算量信仰跑过了。行吧,我也没什么可说的了。
这道题目告诉我们即使再绝望也不要放弃骗分......
(感觉此题堪比以后要给高一考的4e8信仰背包,然而这次却并没有我那么良心的验题人)
考场15分代码:


1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define debug cout 6 using namespace std; 7 const int maxn=1e5+1e2; 8 9 int in[maxn]; 10 int s[maxn],t[maxn<<1],nxt[maxn<<1]; 11 int val[maxn],dis[maxn]; 12 int ans; 13 14 inline int gcd(int a,int b) { 15 if( ! ( a && b ) ) return a | b; 16 register int t; 17 while( t = a % b ) 18 a = b , b = t; 19 return b; 20 } 21 22 inline void addedge(int from,int to) { 23 static int cnt = 0; 24 t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt; 25 } 26 inline void dfs(int pos,int fa) { 27 ans = max( ans , dis[pos] ); 28 for(int at=s[pos];at;at=nxt[at]) 29 if( t[at] != fa ) { 30 int g = gcd(val[pos],in[t[at]]); 31 if( g != 1 ) { 32 dis[t[at]] = dis[pos] + 1 , val[t[at]] = g; 33 dfs(t[at],pos); 34 } 35 } 36 } 37 38 int main() { 39 static int n; 40 scanf("%d",&n); 41 for(int i=1,a,b;i<n;i++) { 42 scanf("%d%d",&a,&b); 43 addedge(a,b) , addedge(b,a); 44 } 45 for(int i=1;i<=n;i++) 46 scanf("%d",in+i); 47 for(int i=1;i<=n;i++) { 48 val[i] = in[i] , dis[i] = 1; 49 dfs(i,-1); 50 } 51 52 printf("%d\n",ans); 53 54 return 0; 55 }
正解代码:


1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #include<map> 7 #include<cmath> 8 #define debug cout 9 using namespace std; 10 const int maxn=1e5+1e2; 11 12 map<int,int> mp; 13 vector<int> pts[maxn<<4]; 14 int in[maxn]; 15 int s[maxn],t[maxn<<1],nxt[maxn<<1]; 16 bool can[maxn],vis[maxn]; 17 int dis[maxn],root,mxp; 18 int n,m,ans,cnt; 19 20 inline void addedge(int from,int to) { 21 static int cnt = 0; 22 t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt; 23 } 24 inline void cut(int x,int p) { 25 int sq = sqrt(x); 26 for(int i=2;i<=sq&&i*i<=x;i++) { 27 if( ! ( x % i ) ) { 28 if( !mp.count(i) ) mp[i] = ++cnt; 29 pts[mp[i]].push_back(p); 30 while( ! ( x % i ) ) x /= i; 31 } 32 } 33 if( x != 1 ) { 34 if( !mp.count(x) ) mp[x] = ++cnt; 35 pts[mp[x]].push_back(p); 36 } 37 } 38 39 inline void dfs(int pos,int fa) { 40 vis[pos] = 1; 41 if( dis[pos] > dis[mxp] ) mxp = pos; 42 for(int at=s[pos];at;at=nxt[at]) 43 if( can[t[at]] && t[at] != fa ) { 44 dis[t[at]] = dis[pos] + 1; 45 dfs(t[at],pos); 46 } 47 } 48 inline void getans(int x) { 49 for(unsigned i=0;i<pts[x].size();i++) 50 can[pts[x][i]] = 1; 51 for(unsigned i=0;i<pts[x].size();i++) 52 if( !vis[pts[x][i]] ) { 53 mxp = 0; 54 dfs(pts[x][i],-1); 55 root = mxp , mxp = 0; 56 dis[root] = 1; 57 dfs(root,-1); 58 ans = max( ans , dis[mxp] ); 59 } 60 for(unsigned i=0;i<pts[x].size();i++) 61 can[pts[x][i]] = vis[pts[x][i]] = dis[pts[x][i]] = 0; 62 } 63 64 int main() { 65 scanf("%d",&n); 66 for(int i=1,a,b;i<n;i++) { 67 scanf("%d%d",&a,&b); 68 addedge(a,b) , addedge(b,a); 69 } 70 for(int i=1,x;i<=n;i++) { 71 scanf("%d",&x); 72 cut(x,i); 73 } 74 75 for(int i=1;i<=cnt;i++) 76 getans(i); 77 78 printf("%d\n",ans); 79 80 return 0; 81 }
然后由于标程复杂度不对,我来补了一发Pollard rho。注意1w以下的数值暴力分解,否则根本跑不出来。还有为什么这玩意跑得比暴力还慢......
无视那个随机数种子什么的,这不重要。
代码:


1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<map> 6 #include<vector> 7 #include<cstdlib> 8 #define lli long long int 9 #define bool unsigned char 10 #define debug cout 11 using namespace std; 12 const int maxn=5e6+1e2; 13 14 int in[maxn],dis[maxn],mxd,root; 15 int s[maxn],t[maxn<<1],nxt[maxn<<1]; 16 bool can[maxn],vis[maxn]; 17 vector<int> pts[maxn]; 18 map<int,int> mp; 19 int n,m,cnt,ans; 20 21 namespace PollardRho { 22 const int lst[15]={0,2,3,5,7,11,13,17,19,23,29,31,61,24251},lstlen=13; 23 inline int fastpow(int base,int tme,int mod) { 24 int ret = 1 , now = base; 25 while( tme ) { 26 if( tme & 1 ) ret = (lli) ret * now % mod; 27 now = (lli) now * now % mod; 28 tme >>= 1; 29 } 30 return ret % mod; 31 } 32 inline bool test(int x,int a) { 33 int p = x - 1 , t = 0; 34 while( ! ( p & 1 ) ) 35 p >>= 1 , ++t; 36 p = fastpow(a,p,x); 37 if( p == 1 || p == x - 1 ) return 1; 38 while( t-- ) { 39 p = (lli) p * p % x; 40 if( p == x - 1 ) return 1; 41 } 42 return 0; 43 } 44 inline bool miller(int x) { 45 for(int i=1;i<=lstlen;i++) 46 if( x == lst[i] )return 1; 47 for(int i=1;i<=lstlen;i++) 48 if( ! ( x % lst[i]) ) return 0; 49 for(int i=1;i<=lstlen;i++) 50 if( !test(x,lst[i]) ) return 0; 51 return 1; 52 } 53 inline int rnd(int x,int mod) { 54 return ( (lli) x * x + 1 ) % mod; 55 } 56 inline int gcd(int a,int b) { 57 if( ! ( a && b ) ) return a | b; 58 register int t; 59 while( t = a % b ) 60 a = b , b = t; 61 return b; 62 } 63 inline void brute(int x,int p) { 64 for(int i=2;i*i<=x;i++) 65 if( ! ( x % i ) ) { 66 if( !mp.count(i) ) mp[i] = ++cnt; 67 pts[mp[i]].push_back(p); 68 while( ! ( x % i ) ) x /= i; 69 } 70 if( x != 1 ) { 71 if( !mp.count(x) ) mp[x] = ++cnt; 72 pts[mp[x]].push_back(p); 73 } 74 } 75 inline void pollard(int x,int p) { 76 if( x <= 10000 ) { 77 brute(x,p); 78 return; 79 } 80 if( miller(x) ) { 81 if( !mp.count(x) ) mp[x] = ++cnt; 82 pts[mp[x]].push_back(p); 83 return; 84 } 85 int g , t1 = rnd(rand(),x) , t2 = rnd(t1,x); 86 while( 1 ) { 87 g = gcd( abs(t1-t2) , x ); 88 if( g != 1 && g != x ) break; 89 t1 = rnd(t1,x) , t2 = rnd(t2,x) , t2 = rnd(t2,x); 90 if( t1 == t2 ) { 91 //srand(time(0)); 92 t1 = rand() % x + 1 , t2 = rand() % x + 1; 93 } 94 } 95 pollard(g,p); 96 pollard(x/g,p); 97 } 98 } 99 using PollardRho::pollard; 100 101 inline void addedge(int from,int to) { 102 static int cnt = 0; 103 t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt; 104 } 105 inline void dfs(int pos,int fa) { 106 vis[pos] = 1; 107 if( dis[pos] > dis[mxd] ) mxd = pos; 108 for(int at=s[pos];at;at=nxt[at]) 109 if( can[t[at]] && t[at] != fa ) { 110 dis[t[at]] = dis[pos] + 1; 111 dfs(t[at],pos); 112 } 113 } 114 inline void solve(const vector<int> &vec) { 115 for(unsigned i=0;i<vec.size();i++) 116 can[vec[i]] = 1; 117 for(unsigned i=0;i<vec.size();i++) { 118 if( vis[vec[i]] ) continue; 119 dis[vec[i]] = 1 , mxd = 0; 120 dfs(vec[i],-1); 121 dis[mxd] = 1; 122 dfs(mxd,-1); 123 ans = max( ans , dis[mxd] ); 124 } 125 for(unsigned i=0;i<vec.size();i++) 126 dis[vec[i]] = vis[vec[i]] = can[vec[i]] = 0; 127 } 128 129 int main() { 130 //srand(5201314); 131 srand(20010128^20010425); 132 scanf("%d",&n); 133 for(int i=1,a,b;i<n;i++) { 134 scanf("%d%d",&a,&b); 135 addedge(a,b) , addedge(b,a); 136 } 137 for(int i=1,x;i<=n;i++) { 138 scanf("%d",&x); 139 pollard(x,i); 140 } 141 142 for(int i=1;i<=cnt;i++) 143 solve(pts[i]); 144 145 printf("%d\n",ans); 146 147 return 0; 148 }
T2:

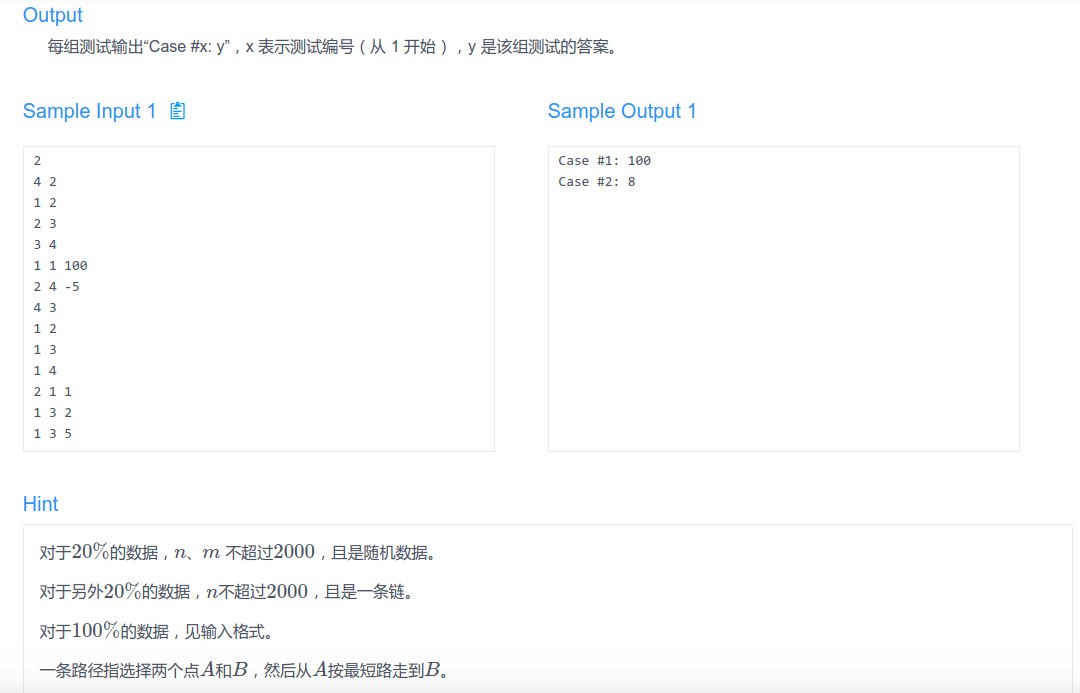
首先呢,这是我完全没有思路的一道题......
正解是把树转化成DFS序,通过各种分类讨论把一对拼图和钥匙的作用范围转化为矩形,然后线段树+扫描线求矩形最大值......
具体题解请见SiriusRen的官方题解:

考场上我当然写了40分暴力啊,结果数据出锅没给暴力分(常数大的都跪了),我暴力爆零了啊......
考场爆零代码(本地测40):


1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 using namespace std; 7 const int maxn=2e3+1e2; 8 const int inf=0x3f3f3f3f; 9 10 vector<int> pics[maxn],keys[maxn]; 11 unsigned char vis[maxn]; 12 int s[maxn],t[maxn<<1],nxt[maxn<<1],cnt; 13 int vals[maxn]; 14 int ans; 15 16 inline void addedge(int from,int to) { 17 t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt; 18 } 19 20 inline void dfs(int pos,int fa,int sum) { 21 for(unsigned i=0;i<keys[pos].size();i++) 22 vis[keys[pos][i]] = 1; 23 for(unsigned i=0;i<pics[pos].size();i++) 24 if( vis[pics[pos][i]] ) sum += vals[pics[pos][i]]; 25 ans = max( ans , sum ); 26 for(int at=s[pos];at;at=nxt[at]) 27 if( t[at] != fa ) 28 dfs(t[at],pos,sum); 29 for(unsigned i=0;i<keys[pos].size();i++) 30 vis[keys[pos][i]] = 0; 31 } 32 33 inline void reset() { 34 memset(s,0,sizeof(s)) , cnt = 0; 35 for(int i=0;i<maxn;i++) 36 keys[i].clear() , pics[i].clear(); 37 ans = -inf; 38 } 39 40 int main() { 41 static int T,n,m; 42 scanf("%d",&T); 43 for(int t=1;t<=T;t++) { 44 reset(); 45 scanf("%d%d",&n,&m); 46 for(int i=1,a,b;i<n;i++) { 47 scanf("%d%d",&a,&b); 48 addedge(a,b) , addedge(b,a); 49 } 50 for(int i=1,p,k;i<=m;i++) { 51 scanf("%d%d%d",&p,&k,vals+i); 52 pics[p].push_back(i) , keys[k].push_back(i); 53 } 54 for(int i=1;i<=n;i++) 55 dfs(i,-1,0); 56 printf("Case #%d: ",t); 57 printf("%d\n",ans); 58 } 59 60 return 0; 61 }
正解代码:


1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #define debug cout 7 using namespace std; 8 const int maxn=6e5+1e2; 9 const int inf=0x3f3f3f3f; 10 11 struct SegmentTree { 12 int l[maxn<<3],r[maxn<<3],lson[maxn<<3],rson[maxn<<3],lazy[maxn<<3],mx[maxn<<3],cnt; 13 14 inline void build(int pos,int ll,int rr) { 15 l[pos] = ll , r[pos] = rr; 16 if( ll == rr ) return; 17 const int mid = ( ll + rr ) >> 1; 18 build(lson[pos]=++cnt,ll,mid); 19 build(rson[pos]=++cnt,mid+1,rr); 20 } 21 inline void add(int pos,int x) { 22 lazy[pos] += x , mx[pos] += x; 23 } 24 inline void push(int pos) { 25 if( lazy[pos] ) { 26 if( lson[pos] ) add(lson[pos],lazy[pos]); 27 if( rson[pos] ) add(rson[pos],lazy[pos]); 28 lazy[pos] = 0; 29 } 30 } 31 inline void update(int pos,int ll,int rr,int x) { 32 if( rr < l[pos] || r[pos] < ll ) return; 33 if( ll <= l[pos] && r[pos] <= rr ) { 34 add(pos,x); 35 return; 36 } 37 push(pos); 38 update(lson[pos],ll,rr,x); 39 update(rson[pos],ll,rr,x); 40 mx[pos] = max( mx[lson[pos]] , mx[rson[pos]] ); 41 } 42 inline int query(int pos,int ll,int rr) { 43 if( rr < l[pos] || r[pos] < ll ) return -inf; 44 if( ll <= l[pos] && r[pos] <= rr ) return mx[pos]; 45 push(pos); 46 return max( query(lson[pos],ll,rr) , query(rson[pos],ll,rr) ); 47 } 48 inline void init() { 49 memset(l+1,0,sizeof(int)*cnt) , memset(r+1,0,sizeof(int)*cnt), 50 memset(lson+1,0,sizeof(int)*cnt) , memset(rson+1,0,sizeof(int)*cnt), 51 memset(lazy+1,0,sizeof(int)*cnt) , memset(mx+1,0,sizeof(int)*cnt); 52 cnt = 0; 53 } 54 }st; 55 56 struct QNode { 57 int x,sy,ty,delta; 58 friend bool operator < (const QNode &a,const QNode &b) { 59 return a.x != b.x ? a.x < b.x : a.delta < b.delta; 60 } 61 }ns[maxn<<3]; 62 int ncnt; 63 64 65 int s[maxn],t[maxn<<1],nxt[maxn<<1],ecnt; 66 int fa[maxn],dep[maxn],siz[maxn],son[maxn],top[maxn]; 67 int dfn[maxn],mxd[maxn],dd; 68 int sum[maxn],key[maxn],pic[maxn],val[maxn]; 69 int n,m,cntm; 70 71 inline void addedge(int from,int to) { 72 t[++ecnt] = to , nxt[ecnt] = s[from] , s[from] = ecnt; 73 } 74 inline void pre(int pos) { 75 siz[pos] = 1; 76 mxd[pos] = dfn[pos] = ++dd; 77 for(int at=s[pos];at;at=nxt[at]) 78 if( t[at] != fa[pos] ) { 79 dep[t[at]] = dep[pos] + 1 , fa[t[at]] = pos; 80 pre(t[at]); 81 mxd[pos] = mxd[t[at]]; 82 siz[pos] += siz[t[at]]; 83 son[pos] = siz[t[at]] > siz[son[pos]] ? t[at] : son[pos]; 84 } 85 } 86 inline void dfs(int pos) { 87 top[pos] = pos == son[fa[pos]] ? top[fa[pos]] : pos; 88 for(int at=s[pos];at;at=nxt[at]) 89 if( t[at] != fa[pos] ) 90 dfs(t[at]); 91 } 92 inline int lca(int a,int b) { 93 while( top[a] != top[b] ) 94 if( dep[top[a]] > dep[top[b]] ) 95 a = fa[top[a]]; 96 else b = fa[top[b]]; 97 return dep[a] < dep[b] ? a : b; 98 } 99 inline int getd(int pos,int l) { 100 int last ; 101 while( top[pos] != top[l] ) 102 last = top[pos] , pos = fa[top[pos]]; 103 if( pos != l ) 104 return son[l]; 105 return last; 106 } 107 108 inline void matrix_add(int sx,int tx,int sy,int ty,int delta) { 109 if( sx > tx || sy > ty ) return; 110 ns[++ncnt] = (QNode){sx,sy,ty,delta} , 111 ns[++ncnt] = (QNode){tx+1,sy,ty,-delta}; 112 } 113 114 inline void reset() { 115 memset(s+1,0,sizeof(int)*ecnt) , memset(fa+1,0,sizeof(int)*n) , 116 memset(dep+1,0,sizeof(int)*n) , memset(siz+1,0,sizeof(int)*n) , 117 memset(son+1,0,sizeof(int)*n) , memset(top+1,0,sizeof(int)*n) , 118 memset(dfn+1,0,sizeof(int)*dd) , memset(mxd+1,0,sizeof(int)*dd), 119 memset(sum+1,0,sizeof(int)*n) , ncnt = cntm = n = m = dd = ecnt = 0; 120 st.init(); 121 } 122 123 inline int solve_node() { 124 int ret = -inf; 125 sort(ns+1,ns+ncnt+1); 126 st.build(st.cnt=1,1,dd); 127 for(int i=1;i<=ncnt;i++) { 128 if( ns[i].x != ns[i-1].x ) { 129 if(i-1) ret = max( ret , st.query(1,1,dd) ); 130 } 131 st.update(1,ns[i].sy,ns[i].ty,ns[i].delta); 132 } 133 return ret; 134 } 135 136 inline int build_matrix() { 137 int ret = 0; 138 for(int i=1;i<=cntm;i++) { 139 const int &a = key[i] , &b = pic[i]; 140 int l = lca(a,b); 141 if( l != a && l != b ) { 142 matrix_add(dfn[a],mxd[a],dfn[b],mxd[b],val[i]); 143 } else { 144 if( l == a ) { 145 int d = getd(b,a); 146 matrix_add(1,dfn[d]-1,dfn[b],mxd[b],val[i]); 147 matrix_add(mxd[d]+1,n,dfn[b],mxd[b],val[i]); 148 } else if( l == b ){ 149 int d = getd(a,b); 150 matrix_add(dfn[a],mxd[a],1,dfn[d]-1,val[i]); 151 matrix_add(dfn[a],mxd[a],mxd[d]+1,n,val[i]); 152 } 153 } 154 } 155 for(int i=1;i<=n;i++) 156 if( sum[i] ) { 157 ret += sum[i]; 158 for(int at=s[i];at;at=nxt[at]) { 159 const int tt = t[at]; 160 if( tt != fa[i] ) { 161 matrix_add(dfn[tt],mxd[tt],dfn[tt],mxd[tt],-sum[i]); 162 } 163 } 164 matrix_add(1,dfn[i]-1,1,dfn[i]-1,-sum[i]); 165 matrix_add(mxd[i]+1,n,mxd[i]+1,n,-sum[i]); 166 matrix_add(1,dfn[i]-1,mxd[i]+1,n,-sum[i]); 167 matrix_add(mxd[i]+1,n,1,dfn[i]-1,-sum[i]); 168 } 169 return ret; 170 } 171 inline int getans() { 172 pre(1) , dfs(1); 173 int preadd = build_matrix(); 174 return preadd + solve_node(); 175 } 176 177 int main() { 178 static int T; 179 scanf("%d",&T); 180 for(int t=1;t<=T;t++) { 181 reset(); 182 scanf("%d%d",&n,&m); 183 for(int i=1,a,b;i<n;i++) { 184 scanf("%d%d",&a,&b); 185 addedge(a,b) , addedge(b,a); 186 } 187 for(int i=1,a,b,v;i<=m;i++) { 188 scanf("%d%d%d",&a,&b,&v); 189 if( a == b ) sum[a] += v; 190 else pic[++cntm] = a , key[cntm] = b , val[cntm] = v; 191 } 192 printf("Case #%d: ",t); 193 printf("%d\n",getans()); 194 195 } 196 197 return 0; 198 }
T3:


此题的重点是:题目的那个"的"字。
首先我们发现2k以内的质数只有300个,并且我们只用考虑奇偶就行。考虑用bitset维护每个数分解后的奇偶状态。
然后我就只会暴力了,手写了一个带<运算符的bitset丢到map里面暴力维护一下就好。
然后发现答案都是2^n-1,找了半天规律没找到,弃坑弃坑。
其实这个东西是线性基。我们考虑对每个质因数列一个方程,把每个数当做元。如果某个数是自由元的话,就证明这个数选和不选都有方案,所以我们可以枚举他选择还是不选。
于是我们对这个矩阵进行高斯消元,答案就是2^自由元个数-1。
当时yzy问我们他有没有讲过线性基,我们说没有,然后......
考场40分代码:


1 #pragma GCC optimize(2) 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 #include<algorithm> 6 #include<bitset> 7 #include<map> 8 #define lli long long int 9 #define debug cout 10 using namespace std; 11 const int maxn=3e2+1e1,maxm=2e3+1e2,lim=2e3; 12 const int mod = 1e9+7; 13 14 struct Pool { 15 unsigned long long dat[5]; 16 const unsigned long long full = 0xffffffffffffffffull; 17 18 inline int getbit(int pos) { 19 int x = pos / 64 , y = pos % 64; 20 return ( dat[x] >> y ) & 1; 21 } 22 inline void revbit(int pos) { 23 int x = pos / 64 , y = pos % 64; 24 dat[x] ^= ( 1ull << y ); 25 } 26 friend Pool operator ^ (const Pool &a,const Pool &b) { 27 Pool ret; 28 for(int i=0;i<5;i++) 29 ret.dat[i] = a.dat[i] ^ b.dat[i]; 30 return ret; 31 } 32 friend bool operator < (const Pool &a,const Pool &b) { 33 for(int i=0;i<5;i++) 34 if( a.dat[i] != b.dat[i] ) return a.dat[i] < b.dat[i]; 35 return 0; 36 } 37 inline void clear() { 38 memset(dat,0,sizeof(dat)); 39 } 40 }dv[maxn]; 41 42 map<Pool,int> mp[2]; 43 lli in[maxn],cpm[maxn]; 44 int prime[maxm],cnt; 45 unsigned char vis[maxm]; 46 int n,cur; 47 48 inline void sieve() { 49 for(int i=2;i<=lim;i++) { 50 if( !vis[i] ) prime[++cnt] = i; 51 for(int j=1;j<=cnt&&i*prime[j]<=lim;j++) { 52 vis[i*prime[j]] = 1; 53 if( !( i % prime[j] ) ) break; 54 } 55 } 56 } 57 58 inline void cut(int p,lli x) { 59 for(int i=1;i<=cnt;i++) 60 while( ! ( x % prime[i] ) ) { 61 dv[p].revbit(i) , x /= prime[i]; 62 } 63 } 64 65 inline void getans() { 66 cur = 0; 67 mp[cur][dv[0]] = 0; 68 for(int i=1;i<=n;i++) { 69 mp[cur^1] = mp[cur]; 70 for(map<Pool,int>::iterator it=mp[cur].begin();it!=mp[cur].end();++it) { 71 Pool tar = it->first ^ dv[i]; 72 mp[cur^1][tar] += it->second , mp[cur^1][tar] %= mod; 73 } 74 mp[cur^1][dv[i]]++ , mp[cur^1][dv[i]] %= mod; 75 cur ^= 1; 76 } 77 } 78 79 inline void clear() { 80 mp[0].clear() , mp[1].clear(); 81 for(int i=0;i<maxn;i++) dv[i].clear(); 82 memset(cpm,0,sizeof(cpm)); 83 } 84 85 86 int main() { 87 sieve(); 88 static int T; 89 scanf("%d",&T); 90 for(int t=1;t<=T;t++) { 91 clear(); 92 scanf("%d",&n); 93 if( n <= 20 ) { 94 for(int i=1;i<=n;i++) { 95 lli x; 96 scanf("%lld",&x); 97 cut(i,x); 98 } 99 getans(); 100 printf("Case #%d:\n",t); 101 printf("%d\n",mp[cur][dv[0]]); 102 } 103 104 } 105 return 0; 106 }
正解代码:


1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<bitset> 6 #define lli long long int 7 using namespace std; 8 const int maxn=3e2+1e1,lim=2e3; 9 const int mod=1e9+7; 10 11 int prime[maxn],cnt; 12 bitset<maxn> bs[maxn]; 13 int n; 14 15 inline void sieve() { 16 static unsigned char vis[lim+10]; 17 for(int i=2;i<=lim;i++) { 18 if( !vis[i] ) prime[++cnt] = i; 19 for(int j=1;j<=cnt&&i*prime[j]<=lim;j++) { 20 vis[i*prime[j]] = 1; 21 if( ! ( i % prime[j] ) ) break; 22 } 23 } 24 } 25 26 inline lli fastpow(lli base,int tme,int mod) { 27 lli ret = 1; 28 while( tme ) { 29 if( tme & 1 ) ret = ret * base % mod; 30 base = base * base % mod; 31 tme >>= 1; 32 } 33 ret = ( ( ret - 1 ) % mod + mod ) % mod; 34 return ret; 35 } 36 37 inline int gauss() { 38 int ret = 0 , used = 0; 39 for(int i=1;i<=n;i++) { 40 int pos = -1; 41 for(int j=used+1;j<=cnt;j++) 42 if( bs[j][i] ) { 43 pos = j; 44 break; 45 } 46 if( !~pos ) { 47 ++ret; 48 continue; 49 } 50 swap(bs[pos],bs[++used]); 51 for(int j=1;j<=cnt;j++) 52 if( j != used && bs[j][i] ) 53 bs[j] ^= bs[used]; 54 } 55 return ret; 56 } 57 58 inline void cut(int p,lli x) { 59 for(int i=1;i<=cnt;i++) 60 while( ! ( x % prime[i] ) ) 61 bs[i][p] = !bs[i][p] , 62 x /= prime[i]; 63 } 64 65 inline void init() { 66 for(int i=0;i<maxn;i++) 67 bs[i] &= 0; 68 } 69 70 int main() { 71 static int T; 72 sieve(); 73 scanf("%d",&T); 74 for(int t=1;t<=T;t++) { 75 init(); 76 scanf("%d",&n); 77 for(int i=1;i<=n;i++) { 78 lli x; 79 scanf("%lld",&x); 80 cut(i,x); 81 } 82 printf("Case #%d:\n",t); 83 printf("%lld\n",fastpow(2,gauss(),mod)); 84 } 85 return 0; 86 }
本次考试并不是题的问题,主要还是我太菜。T1完全可以特判范围采用那种暴力,即使不能AC也能多骗点分吧,T3如果仔细想想也是可以做出来的,T2的暴力,如果没有用vector而是选择挂链,少打几个头文件的话估计也是能有分的(卡常这个事可能谁也救不了我了)。(T2正解DFS序转矩阵+分类讨论脑洞太大想不出来算了)
最后附上rank榜,这次题目变成这样也是没谁了。



)







...)

)

![[转] Java, 使用 Reactor 进行反应式编程](http://pic.xiahunao.cn/[转] Java, 使用 Reactor 进行反应式编程)




