python 数据结构与算法

1 python常见数据结构性能

1.1 List

1.1.1 安索引取值和赋值

1.1.2 列表append和__add__()

1.1.3 使用timeit模块测试执行时间

1.1.4 List基本操作的大O数量级

1.2 Dict

1.2.1 dict数据类型

2 线性结构 Linear Structure

2.1 栈Stack

2.1.1 抽象数据类型Stack

2.1.2 Stack的操作如下

2.1.3 栈的应用1：简单括号匹配

2.1.3.1 圆括号匹配

2.1.3.2 通用括号匹配

2.1.4 栈的应用2：进制转换

2.1.4.1 十进制转换二进制

2.1.4.2 十进制转换任意进制

2.1.5 栈的应用3：表达式转换

2.1.5.1 中缀表达式

2.1.5.2 全括号中缀表达式

2.1.5.3 前缀和后缀表达式

2.1.5.4 中缀表达式转换为前缀和后缀形式

2.1.5.5 通用的中缀转后缀算法

2.1.5.6 后缀表达式求值

2.2 队列Queue

1 python常见数据结构性能

1.1 List

1.1.1 安索引取值和赋值

list最常用的操作是：按索引取值和赋值(v=a[i]，a[i]=v)，这两个操作执行时间与列表大小无关，均为O(1)。

1.1.2 列表append和__add__()

list.addend(v)，执行时间是O(1)。

list0 = list1 + [v]，执行时间是O(n+k)，其中k是被加的列表长度。

1.1.3 使用timeit模块测试执行时间

使用timeit模块对函数计时：

1.1.4 List基本操作的大O数量级

1.2 Dict

1.2.1 dict数据类型

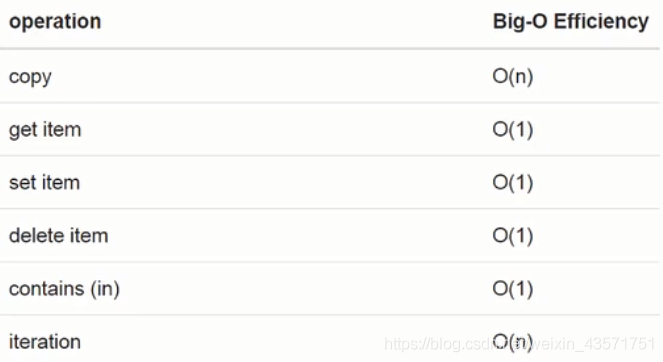
字典是根据key找到对应的value，最常用的取值get和赋值set，其性能都是O(1)。另外一个常用的操作判断字典中是否存在某个key (in)，这个性能也是O(1)。

2 线性结构 Linear Structure

线性结构是一种有序数据项的集合，其中每个数据项都有唯一的前驱和后继(除了第一个和最后一个)。

2.1 栈Stack

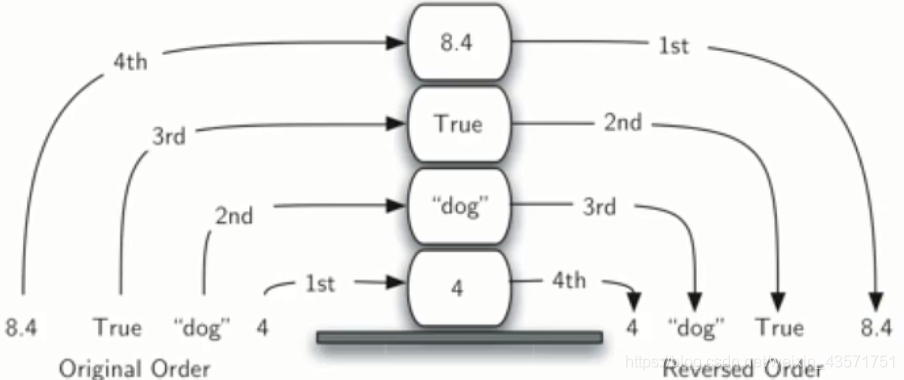
栈是一种有次序的数据项集合，在栈中，数据项的加入和移除都仅发生在同一端，这一端叫做“栈顶top”，另一端叫做“栈底base”。

栈是一种后进先出LIFO：Last in First out，这是一种基于数据项保存时间的次序，时间越短的离栈顶越近，而时间越长的离栈底越近。

2.1.1 抽象数据类型Stack

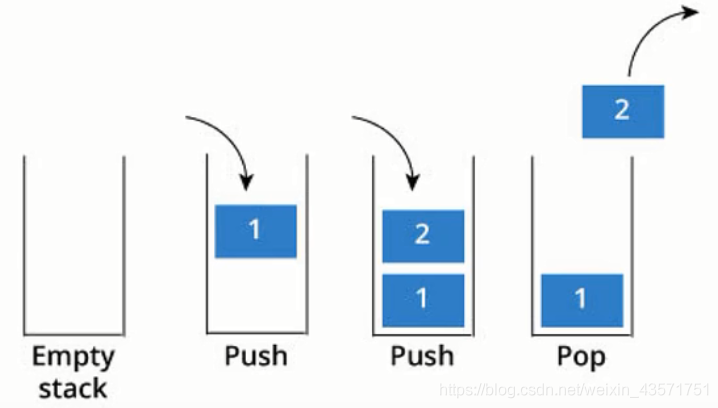
抽象数据类型“栈”是一个有次序的数据集，每个数据项仅从“栈顶”一端加入到数据集中、从数据集中移除，栈具有后进先出LIFO的特性。

2.1.2 Stack的操作如下

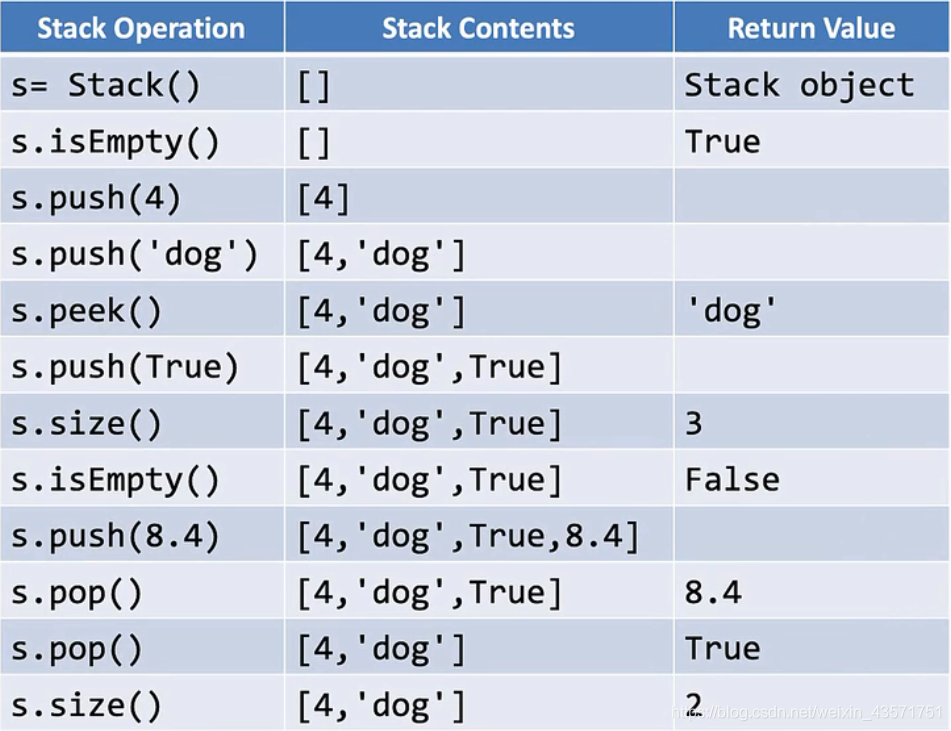
stack()：创建一个空栈，不包含任何数据项。

push(item)：将item加入栈顶，无返回值。

pop()：将栈顶的数据项移除，并返回，栈被修改。

peek()：“窥视”栈顶数据项，返回栈顶的数据。

isEmpty()：返回是否是空栈。

size()：返回栈中有多少个数据项。

class Stack(object):

def __init__(self):

self.stack = []

def push(self, item):

self.stack.append(item)

def pop(self):

if not self.is_empty():

return self.stack.pop()

def peek(self):

if not self.is_empty():

return self.stack[self.size()-1]

def is_empty(self):

return len(self.stack) == 0

def size(self):

return len(self.stack)

2.1.3 栈的应用1：简单括号匹配

2.1.3.1 圆括号匹配

括号必须遵循“平衡”原则，即每个开括号必须有一个比括号对应。

从左到右扫描括号，最新打开的左括号，应该匹配最先遇到的右括号。这样，第一个左括号就应该匹配最后一个右括号，这种次序反转的识别，正好符合栈的特性。

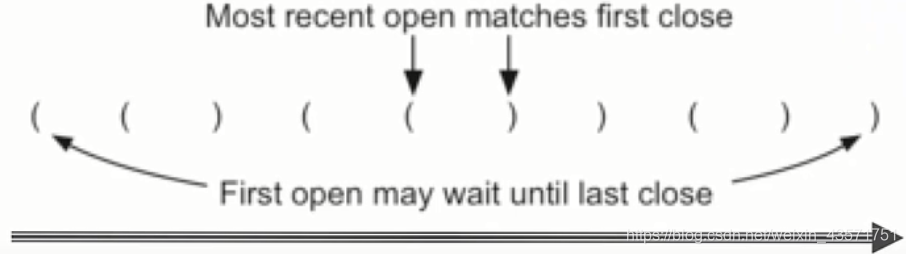
流程图如下：

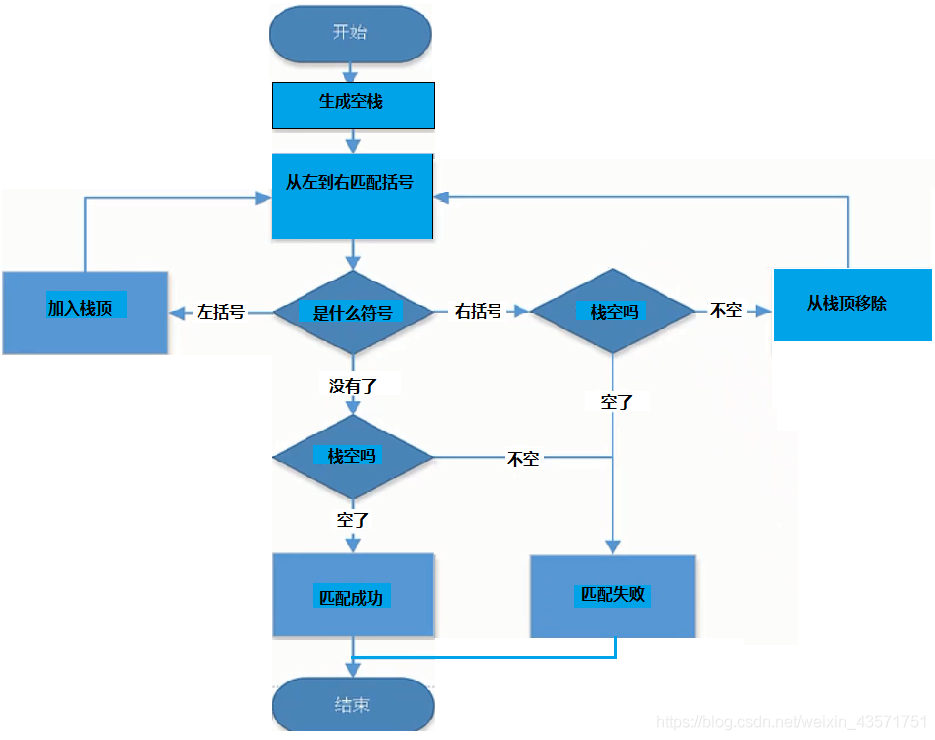
from data_structure.Stack.stack import Stack

def brackets_valid(expression):

stack = Stack()

for item in expression:

if item == "(":

stack.push(item)

elif item == ")":

if stack.is_empty():

return False

else:

stack.pop()

return stack.is_empty()

if __name__ == '__main__':

print(brackets_valid("()()()"))

print(brackets_valid("(()())(()"))

print(brackets_valid("((5+6)*(4+3))+((10-9)"))

2.1.3.2 通用括号匹配

实际应用中，会遇到更多种括号，比如：[], {},()。

from data_structure.Stack.stack import Stack

def brackets_valid(expression):

stack = Stack()

mapping = {

")": "(",

"]": "[",

"}": "{"

}

for item in expression:

if item in "([{":

stack.push(item)

elif item in ")]}":

if stack.is_empty():

return False

else:

if stack.peek() != mapping[item]:

return False

else:

stack.pop()

return stack.is_empty()

if __name__ == '__main__':

print(brackets_valid("()()()"))

print(brackets_valid("(()())(()"))

print(brackets_valid("((5+6)*(4+3))+((10-9)"))

print(brackets_valid("{{([][])}()}"))

print(brackets_valid("[[{{(())}}]]"))

print(brackets_valid("[][][](){}"))

print(brackets_valid("([)}"))

print(brackets_valid("((()]))"))

print(brackets_valid("[{()]"))

2.1.4 栈的应用2：进制转换

进制：指用多少字符来表示整数。十进制是0-9十个数字字符，二进制是0、1两个字符。

例如：十进制233对应的二进制是11101001，具体算法如下：

233 = 2102 + 3101 + 3100

11101001 = 127 + 126 + 125 + 024 + 123 + 022 +021 + 1*20

2.1.4.1 十进制转换二进制

常见的十进制转换二进制采用的是**“除2求余数”的算法。如下：35的二进制是100011。在除2求余的过程中，得到的余数是从低到高的次序，而输出则是从高到低，所以需要一个栈来反转次序**。

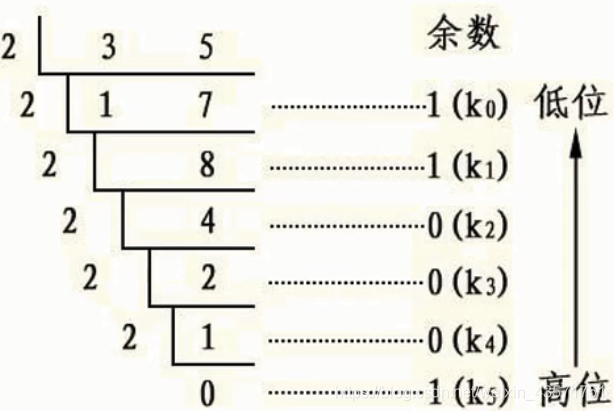
from data_structure.Stack.stack import Stack

def convert(num):

if not isinstance(num, int):

return False

stack = Stack()

while num:

num, remainder = divmod(num, 2)

stack.push(remainder)

result = ""

while not stack.is_empty():

result += str(stack.pop())

return result

if __name__ == '__main__':

print(f"35的二进制数是{convert(35)}")

2.1.4.2 十进制转换任意进制

将“除2求余”改为“除N求余”就可以将上面的算法扩展为任意进制转换。

十进制233对应八进制351，十六进制是E9。

主要区别是：

二进制：0-1

十进制：0-9

八进制：0-7

十六进制：0-9，A-F

from data_structure.Stack.stack import Stack

def convert(num, unit):

if not isinstance(num, int):

return False

dights = "0123456789ABCDEF"

stack = Stack()

while num:

num, remainder = divmod(num, unit)

stack.push(remainder)

result = ""

while not stack.is_empty():

result += str(dights[stack.pop()])

return result

if __name__ == '__main__':

print(f"35的二进制数是{convert(35, 2)}")

print(f"233的八进制数是{convert(233, 8)}")

print(f"233的十六进制数是{convert(233, 16)}")

2.1.5 栈的应用3：表达式转换

2.1.5.1 中缀表达式

操作符位于两个操作数之间的表示法，称为“中缀”表达式。例如：A+B。

2.1.5.2 全括号中缀表达式

计算机处理时最好避免复杂的优先级(乘除优先于加减、括号优先级)规则，能明确规定所有的计算顺序是最好的。因此，引入全括号表达式： ((A+B*C)+D)

2.1.5.3 前缀和后缀表达式

前缀表达式：将操作符移到操作数前面，即：+AB。

后缀表达式：将操作符移到操作数后面，即：AB+。

在前缀和后缀表达式中，操作符次序完全决定了运算的次序，不再混淆。

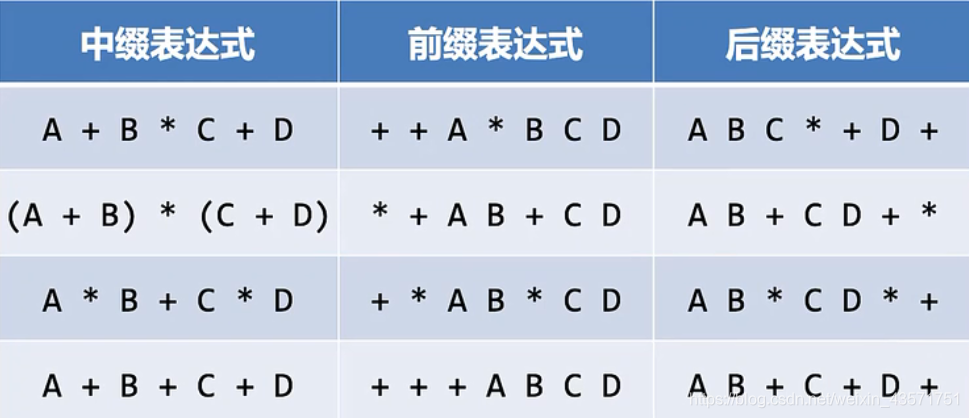
2.1.5.4 中缀表达式转换为前缀和后缀形式

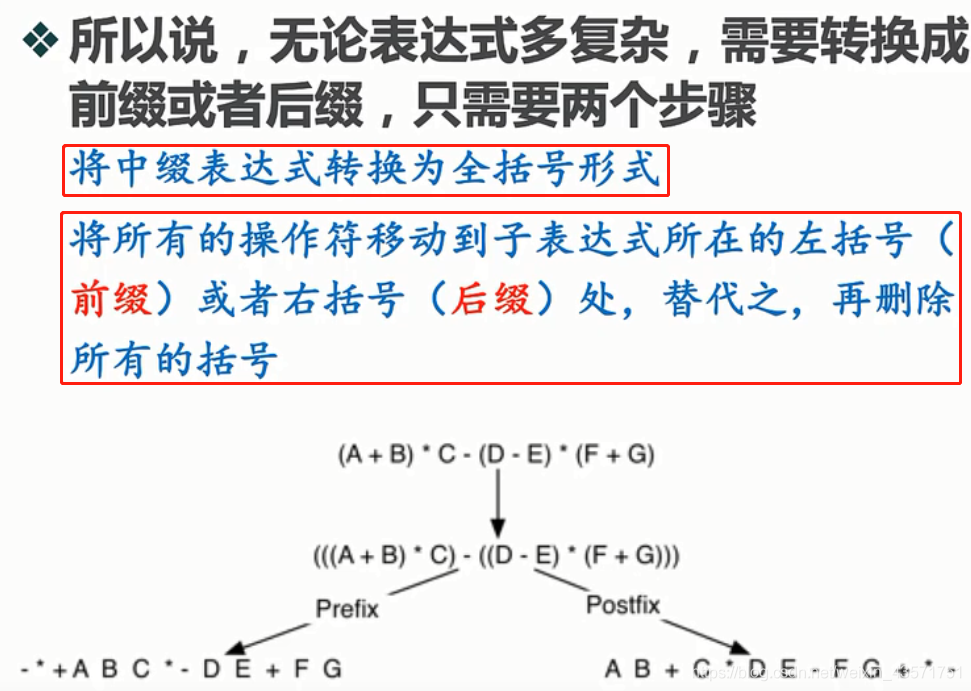
2.1.5.5 通用的中缀转后缀算法

中缀表达式A+BC，对应的后缀表达式是 ABC+。其中，操作数ABC的顺序没有改变，操作符的出现顺序在后缀表达式中反转了。由于*的优先级比+高，所以后缀表达式中操作符的出现顺序与运算次序一致。

算法流程：

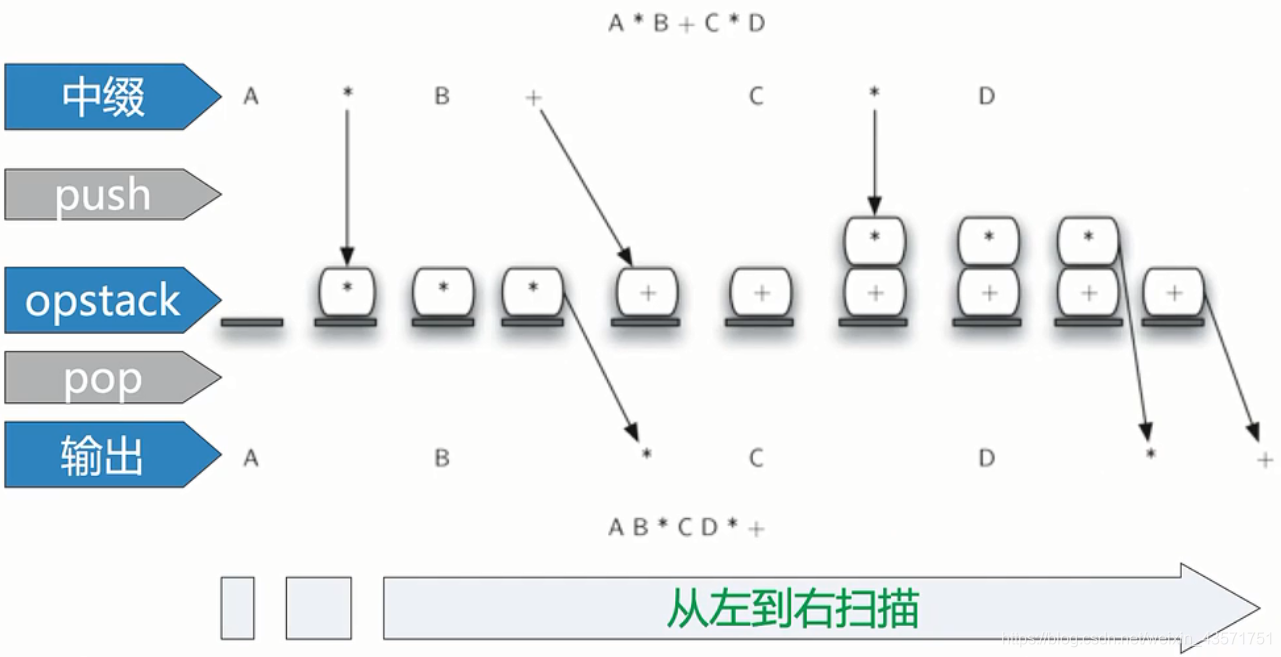
import string

from data_structure.Stack.stack import Stack

def convert_postfix(expression):

result = ""

oper_stack = Stack()

priority = {

"(": 0,

"+": 1,

"-": 1,

"*": 2,

"/": 2

}

for item in expression:

if item in string.ascii_letters or item in string.digits:

result += item

elif item == "(":

oper_stack.push(item)

elif item == ")":

while oper_stack.peek() != "(":

result += oper_stack.pop()

else:

oper_stack.pop()

elif item in "+-*/":

while oper_stack.peek() and \

priority[oper_stack.peek()] >= priority[item]:

result += oper_stack.pop()

else:

oper_stack.push(item)

while not oper_stack.is_empty():

result += oper_stack.pop()

return result

if __name__ == '__main__':

print(convert_postfix("A+B*C"))

print(convert_postfix("(A+B)*C"))

2.1.5.6 后缀表达式求值

对于后缀表达式从左到右扫描，由于操作符在操作数后面，所以要暂存操作数，在遇到操作符的时候再将暂存的两个操作数进行实际的计算。

例如： ABC*+，先扫描到了ABC暂存到栈中，扫描到*的时候，从栈中弹出2个操作数做乘法，做完之后再存入栈中；继续扫描到+，从栈中弹出2个操作数做加法。

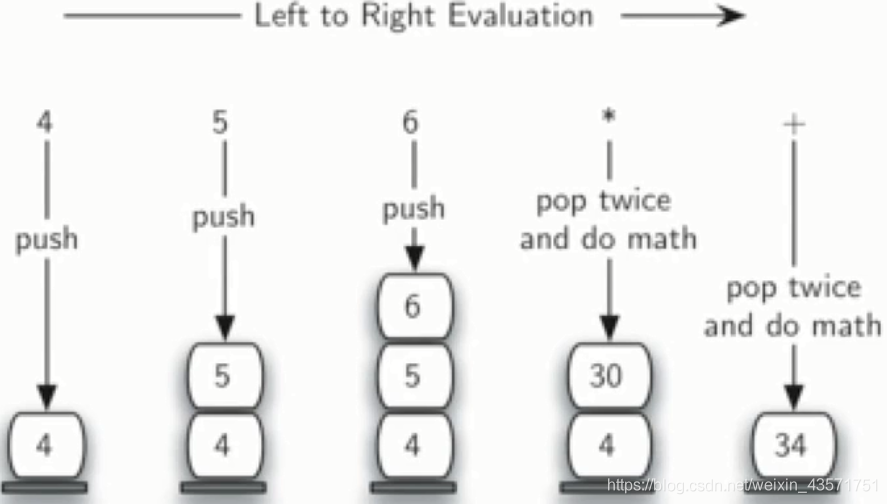
注意：对于-/操作符，弹出的两个操作数顺序很重要，先弹出的是右操作数，后弹出的是左操作数。

算法流程：

import string

from data_structure.Stack.stack import Stack

from data_structure.Stack.infix_to_postfix import convert_postfix

def calculate(expression):

stack = Stack()

for item in expression:

if item in string.digits:

stack.push(item)

elif item in "+-*/":

first = stack.pop()

second = stack.pop()

stack.push(str(eval(second + item + first)))

return stack.pop()

if __name__ == '__main__':

print(calculate(convert_postfix("1+2*3")))

print(calculate(convert_postfix("(1+2)*3")))

2.2 队列Queue