指令的存储与执行初探

前言导读：从零开始构造一台二进制加法器

假设一个处理器与存储器相连，存储器中存放着一些指令。这些指令通过处理器发出的寻址信号被加载到处理器中，这个过程称为取指令。

下面通过简单的加法运算，来看一下指令和数据是怎么存储在RAM中的。

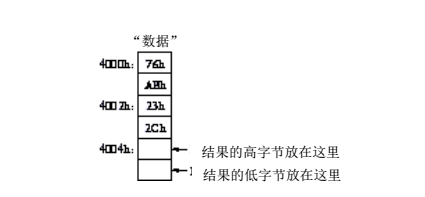
如果要将76ABh和236Ch相加，先将这两个加数存储在数据RAM中如下：

这是两个加数存储在RAM中的位置，为了方便运算，将高低字节分别存储。可以看到这个RAM存储器的最小存储单元是一个字节，地址是一个16位地址，所以这个RAM总共由2的16次方个小的8位RAM组成：即该RAM的大小为64K*8。

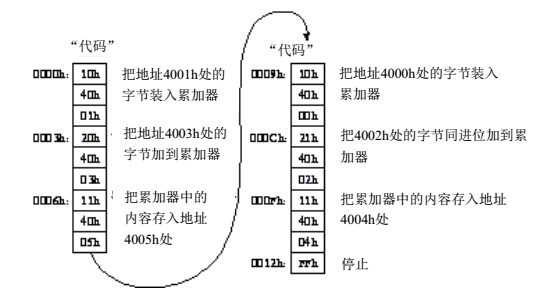
说完了数据的存储情况，再看一下代码的存储情况：

实现该设计的关键是，将这些代码输出到3个不同的寄存器中保存。第一个寄存器保存代码本身，第二个寄存器保存地址的高字节，第三个寄存器保存地址的低字节。第二个和第三个寄存器的输出构成了数据RAM的一个16位地址。

取指令在这里就是指的寻址RAM，将代码RAM中的指令放进加法器中执行。在这里一条指令有3个字节，所以取每条指令需要3个时钟周期，由于第二位和第三位寄存器中保存的是RAM中的一个地址，所以在取到这个地址后还需要取RAM的相应地址，以获得该地址上的数据。所以一个完整的指令周期在这里需要4个时钟周期。

现在我们使用的是3字节长的指令格式，第二个字节和第三个字节用来指明操作数在RAM中的存储地址，为了方便，完全没有必要取分数据RAM和代码RAM。

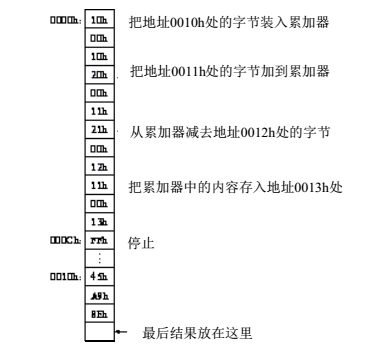
例如，现在这里有一个算术运算：45h+A9h-8Eh。如何通过指令代码来描述这个运算？

从0000h到000Ch都是指令代码，从0010h开始的3个存储单元，存放的是操作数据。可以看到在同一个RAM上已经完全可以描述一个算术运算。

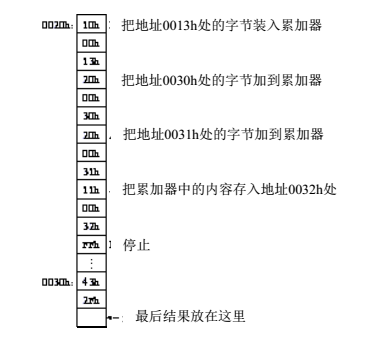
此时，如果需要在原来的运算结果基础上再加上两个数：45h+A9h-8Eh+43h+2Fh。

有两种做法：

第一种就是从0000h开始，向存储器中输入新的指令以替换原来所有的指令，这种方式不需要懂任何脑筋，是最笨的方法，就像你从北京出发去南京旅游，到了南京以后突然改变主意，想去上海，然后你又回到北京，买了北京到上海的票。

第二种做法利用了前面的计算结果，接着做计算，这才是正常的思路。先将000Ch处的halt指令去掉，从000Ch开始加上新增的两条add指令和halt指令，可是这样的话新增的指令会覆盖掉从0010h处开始存放的原来的数据。于是又有另一种方法，能不能从0014h以后的某片RAM区域开始，存放新的指令以及数据，这时两片区域是不连续的：

在这里假设从0020h开始加上新的指令以及数据，可是问题又来了，要知道程序计数器是从0000h开始顺序递增的，不会从一个地址跳到另外一个不相邻的地址，要想实现跳转的功能，得从硬件层面对计数器进行改进，这是可以实现的，具体的方法这里就不展开叙述了。

通过对计数器的改进，我们新增了一条指令：Jump指令。即加法器（此时的加法器可以理解为一个简易的CPU，它会去执行从RAM中读取到的指令）一执行到Jump指令，改造后的计数器就会被强制输出该Jump指令后的16位地址值，代码的执行不再是顺序执行。

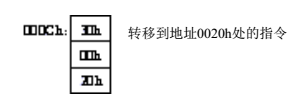
将原来000Ch处的halt指令修改如下：

当pc运转到000Ch的时候，被强制输出0020h，即代码跳到0020h开始接着执行。在硬件层面上这只是一个很小的改动，可是对于代码的执行而言，是一个很大的改进。有了Jump指令，我们就可以在RAM存储空间中自由的跳转，其实相比较于跳转指令，我们更需要的是让跳转指令在某个条件下才执行。

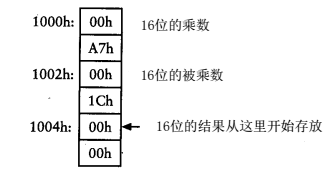
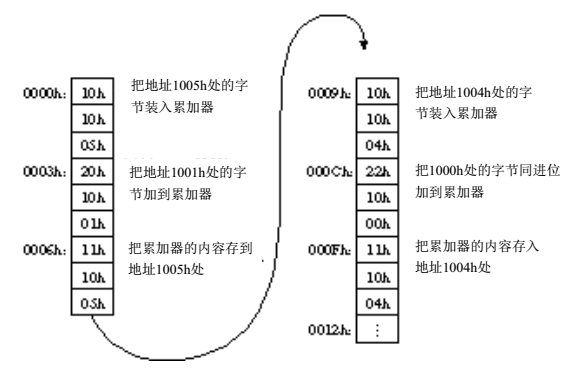
例如，现在有一个乘法运算：00A7h*001Ch。小学生都学过，乘法运算的实质就是加法运算，即00A7h和001Ch相乘的结果和把001Ch（十进制为28）个00A7h累加的结果相同。

可以看到，从0000h开始到0012h，使RAM地址1004h和1005h里面保存的值是00A7h乘以1的结果。如果将这段区间的指令重复28次，当然可以得到想要的乘法运算结果，可是这种方法挺笨的。

如果用到之前提过的一个新指令，就是在0012h处放置一条Jump。

这样确实能让代码不断的重复，但是这样会有一个问题，0000h到0012h之间的指令会永远重复的执行，因为没有一条halt指令让它停下来。这时其实我们需要的是一种条件跳转指令，就是让某段指令重复指定的次数，一旦达到某个值，就不重复了。要实现条件跳转，还是先得从硬件层面进行优化：

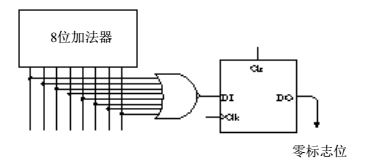
首先新增一个一位锁存器，该锁存器称为零锁存器，将该锁存器与加法器和或非门连接如下：

只有当上一步操作是add、subtract、add with carry、subtract with borrow时，零锁存器才会存住一个数，至于这个数是0还是1，就要看上一步操作的输出是什么了。如果加法器的8位输出全为0时，零锁存器里的值为1。如果加法器8位输出有一个为1，零锁存器里的值就是0。

现在通过对硬件的改进，新增了下面四种跳转指令：

• Jump If Zero（零跳转）
• Jump If Carry（进位跳转）
• Jump If Not Zero（非零跳转）
• Jump If Not Carry（非进位跳转）

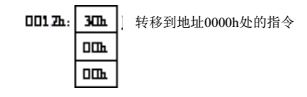
要实现乘法运算，我们使用一个非零跳转，对应的指令码为33h。

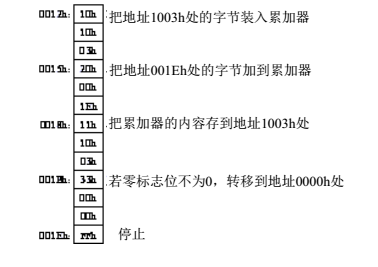
将0012h后的指令设计如下：

这一段指令执行的操作是，将001Ch（其中一个乘数）与00FFh相加，这两个数相加的结果其实就等同于从001Ch中减一的结果，如果是第一次执行，这个结果为001Bh，所以加法器的输出不全为0，执行非零跳转，跳转到0000h处开始继续执行下一轮加法运算，所以上面这段代码其实起到了一个计数的功能，记录了当前的累加执行到哪一次了，当执行完最后一次类加，1003h里保存的值是0001h，加上00FFh后，结果为0，即加法器的输出全为零，所以不会执行非零跳转指令，而是接着执行001Eh中的halt指令（注意：这个地址里的FFh，我们既可以把它当作一个普通的二进制数，也可以把它当作一个halt指令）。

还需要特别注意的是，这里的非零跳转中的非零指的是加法器的输出非零，而不是指的锁存器里的值非零与否。如果把非零理解为零锁存器中的值的话，逻辑就完全相反了。

至此我们通过一个新增的指令，在加法的基础上完成了乘法的操作。

通过不断的硬件完善，特别是加上条件跳转指令后，已经具备了计算机的雏形。能否控制循环是计算器与计算机的区别。上面演示了如何通过条件跳转实现乘法运算，用类似的方法还能实现除法运算，甚至是开平方、取对数、三角函数等等也完全可以实现，只不过相对复杂一些。