题目大意
给出一个$w\times h$的网格,定义一个连通块为一个元素个数为$n$的方格的集合$A,\forall x\in A, \exists y\in A$,使得$x,y$有一条公共边。现要求一个元素个数极多的连通块的集合$K_N$,使得$\forall A,B\in K_n$,不存在一种由对称、旋转、平移组成的操作$f(A)$,使得$f(A)=B$。求$|K|$。$w\leq h\leq n\leq 10$。
题解
这道题可把我恶心到吐了。。。
主体算法
错误算法1
跟宝藏一题的思路一样,把两个相邻的块看作由一条边连接的两个节点,随后枚举生成树的个数$m$即可。最后输出的结果便是$\frac{m}{8}$(对称/2,旋转再/4)。
这种做法错因在于不同的连通块可以对应不同的生成树,而且连通块可能会有轴对称或旋转对称等。以后遇到像这样复杂得连手推样例都不愿做的算法就不要再使用了。
错误算法2
对于每一组数据,进行Dfs搜索。将Dfs搜索到的连接块用set记录,它的作用一是防止一个连通块被访问多次。二是防止等价的最终连通块使答案变多,实现是要将最终连通块本身以及经过对称旋转后的变化图形卡在网格的左上角。
这种做法错在多组数据都要重算一遍,时间复杂度太高。
正确算法
我们运用打表的思想,Bfs将$10\times 10$网格内的$K_n, n=1,2,\cdots 10$全部预处理出来保存在set<Block> Ans[15]中,给出$n,w,h$,则在Ans[n]中找到符合条件(注意:对于长径和宽径不同的连通块,不但要看看正常放能不能放入网格中,还要看看把它旋转90°后能不能放入)的连通块即可。
怎么Bfs呢?Bfs的每一层按照连通块内格子的个数进行分类。Bfs的起点是一个只有格子(1, 1)的连通块。每一个Ans[n]内的连通块都是恰好卡到左上角的连通块。Ans[i]由Ans[i - 1]扩展得来,对于Ans[i - 1]中的每个连通块$A$,尝试找出两个相邻的网格$a, b, a\in A, b\notin A$,若它经过各种变换后的图形在Ans[i]中都没有出现,则将该连通块加入Ans[i]。
问题来了,如何处理下列情况呢?

如果我们就在网格的限制内扩展,这种扩展就不可能。所以我们可以尝试扩展到整个网格以外,然后卡到左上角的方法达到这个目的。因为每次只扩展一个格子,所以这种方法可行。
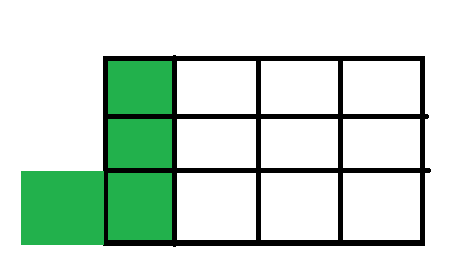
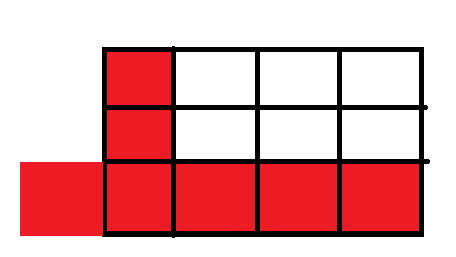
不过这时我们不要忘了特判不合法的情况:
矩阵操作
方法一
在每个连通块内维护一个set,维护每个在连通块内的网格的坐标。
这样处理有些麻烦。
方法二
每个连通块用二维数组存储,变换以整个网格的某个位置作为中心或轴。
这个时候旋转90°操作就比较膈应人了。我们不可以以整个网格的中心作为轴,因为。。。待会,到底是旋转到哪儿去?中心是哪儿? 我们不如直接以(0, 0)作为中心旋转,将旋转过后的坐标用vector存储起来,然后将vector内的所有网格(row, col)加上(dRow, dCol)再存储起来。
这种做法就是感觉有些不专业。。。
最终做法
每个连通块用二维数组存储,操作在连通块所在矩形内操作。
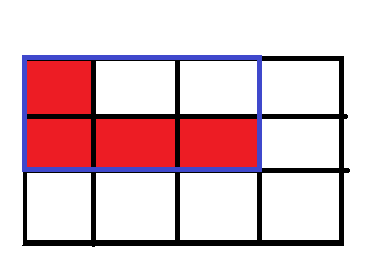
如图蓝色的矩形即为红色连通块对应的矩形。
此时如何旋转90°呢?我们要用矩阵转置的方法。
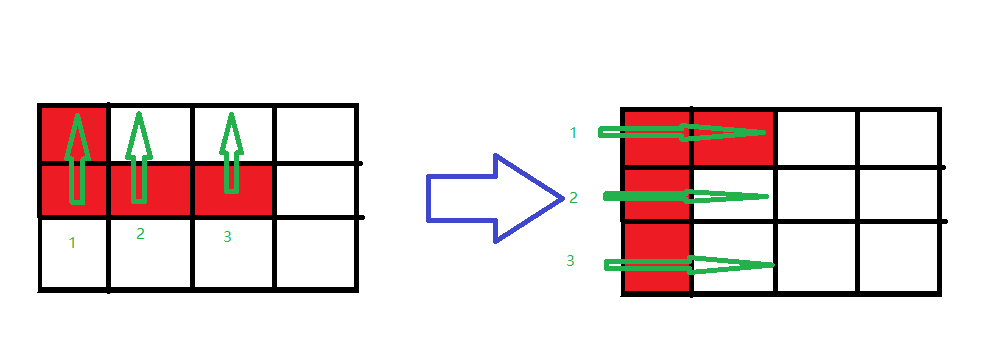
然后这个程序就在50ms内通过了。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <set>
#include <cassert>
using namespace std;#define UpdateMin(x, y) x = min(x, y)
#define UpdateMax(x, y) x = max(x, y)const int MAX_POS_ARG_SIZE = 15, INF = 0x3f3f3f3f, MINF = 0xcfcfcfcf;
const int TotRow = 10, TotCol = 10, TotNode = 10;
const int Dir[4][2] = { {0, 1}, {1, 0}, {0, -1}, {-1, 0} };struct Block
{bool A[MAX_POS_ARG_SIZE][MAX_POS_ARG_SIZE];Block(){memset(A, 0, sizeof(A));}bool operator < (const Block& a) const{return memcmp(A, a.A, sizeof(A)) == -1;}bool operator == (const Block& a) const{return memcmp(A, a.A, sizeof(A)) == 0;}Block operator = (const Block& a){memcpy(A, a.A, sizeof(A));return *this;}void GetRect(int &minRow, int &maxRow, int &minCol, int &maxCol)//所在矩形{minRow = minCol = INF;maxRow = maxCol = MINF;for (int row = 0; row <= TotRow; row++)for (int col = 0; col <= TotCol; col++)if (A[row][col]){UpdateMin(minRow, row);UpdateMax(maxRow, row);UpdateMin(minCol, col);UpdateMax(maxCol, col);}}void GetSq(int &minRow, int &maxRow, int &minCol, int &maxCol)//所在正方形{GetRect(minRow, maxRow, minCol, maxCol);int eLen = max(maxRow - minRow + 1, maxCol - minCol + 1);maxRow = minRow + eLen - 1;maxCol = minCol + eLen - 1;}Block GetFlipHor(){Block ans;int minRow, maxRow, minCol, maxCol;GetRect(minRow, maxRow, minCol, maxCol);for (int row = minRow; row <= maxRow; row++)for (int col1 = minCol, col2 = maxCol; col1 <= maxCol; col1++, col2--)ans.A[row][col2] = A[row][col1];return ans;}Block GetRotate90(){Block ans;int minRow, maxRow, minCol, maxCol;GetRect(minRow, maxRow, minCol, maxCol);for (int row = 1; row <= maxCol; row++)for (int col = 1; col <= maxRow; col++)ans.A[row][col] = A[maxRow -col +1][row];return ans;}Block GetNormal(){Block ans;int minRow, maxRow, minCol, maxCol;GetRect(minRow, maxRow, minCol, maxCol);for (int row = minRow; row <= maxRow; row++)for (int col = minCol; col <= maxCol; col++)ans.A[row - minRow + 1][col - minCol + 1] = A[row][col];return ans;}bool Invalid(int totNode){int minRow, maxRow, minCol, maxCol;GetRect(minRow, maxRow, minCol, maxCol);return maxRow - minRow + 1 > totNode || maxCol - minCol + 1 > totNode;}
};set<Block> Ans[MAX_POS_ARG_SIZE];bool Exists_Rotate(set<Block> &ans, Block cur)
{if (ans.count(cur))return true;for (int i = 1; i <= 3; i++){cur = cur.GetRotate90();if (ans.count(cur))return true;}return false;
}bool Exists(set<Block> &ans, Block cur)
{if (Exists_Rotate(ans, cur))return true;if (Exists_Rotate(ans, cur.GetFlipHor().GetNormal()))return true;return false;
}void MakeAnsList()
{Block start;start.A[1][1] = true;Ans[1].insert(start);for (int i = 2; i <= TotNode; i++){for (set<Block>::iterator it = Ans[i - 1].begin(); it != Ans[i - 1].end(); it++){for (int row = 1; row <= TotRow; row++)for (int col = 1; col <= TotCol; col++){if (it->A[row][col]){for (int k = 0; k < 4; k++){int nextRow = row + Dir[k][0], nextCol = col + Dir[k][1];if (nextRow < 0 || nextRow > TotRow || nextCol < 0 || nextCol > TotCol)continue;if (it->A[nextRow][nextCol])continue;Block next = *it;next.A[nextRow][nextCol] = true;if (next.Invalid(i))continue;next = next.GetNormal();if (Exists(Ans[i], next))continue;Ans[i].insert(next);}}}}}
}int GetAns(int totNode, int totRow, int totCol)
{int ans = 0;for (set<Block>::iterator it = Ans[totNode].begin(); it != Ans[totNode].end(); it++){Block temp = *it;int minRow, maxRow, minCol, maxCol;temp.GetRect(minRow, maxRow, minCol, maxCol);assert(minRow == 1 && minCol == 1);if (maxRow <= totRow && maxCol <= totCol || maxCol <= totRow && maxRow <= totCol){Block a = *it;ans++;}}return ans;
}int main()
{MakeAnsList();int totNode, totRow, totCol;while (~scanf("%d%d%d", &totNode, &totRow, &totCol))printf("%d\n", GetAns(totNode, totRow, totCol));return 0;
}
















)


