poj 1330 Nearest Common Ancestors LCA/DFS

题目链接:

http://poj.org/problem?id=1330

题意:

求出两点间的最近公共祖先。

题解:

第一种：
并查集维护：http://www.cnblogs.com/procedure2012/archive/2012/01/29/2331468.html
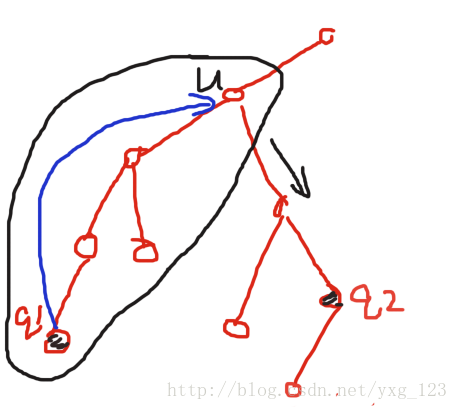
利用并查集在每次对子树进行遍历时进行合并，因为对以x为根的子树的遍历时只有当x的所有子树都遍历过后才会把它合并到他父亲的集合里，所以当需要查找的两个节点q1、q2中q1已被遍历且q2正是当前遍历的节点时说明此时只有距他们最近的祖先是在集合里的（可能为q1或q2），所以只要找到已被遍历的q1所在集合的祖先就是这两的节点的LCA。
这里写图片描述

第二种
直接dfs：每次从u和v的depth较深的开始往上面找，然后如果一样就跳出，不一样继续找

代码:

并查集

 1 #include <cstdio>
 2 #include <cstring>
 3 #include <iostream>
 4 #include <algorithm>
 5 #include <vector>
 6 using namespace std;
 7 typedef long long ll;
 8 #define MS(a) memset(a,0,sizeof(a))
 9 #define MP make_pair
10 #define PB push_back
11 const int INF = 0x3f3f3f3f;
12 const ll INFLL = 0x3f3f3f3f3f3f3f3fLL;
13 inline ll read(){
14     ll x=0,f=1;char ch=getchar();
15     while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
16     while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
17     return x*f;
18 }
19 //
20 const int maxn = 1e4+10;
21 
22 vector<int> g[maxn];
23 int f[maxn],vis[maxn],fa[maxn];
24 int q1,q2;
25 int a[maxn];
26 
27 int find(int x){
28     return fa[x]==x ? x : fa[x]=find(fa[x]);
29 }
30 
31 void Union(int x,int y){
32     int p1=find(x),p2=find(y);
33     if(p1 == p2) return ;
34     fa[p1] = p2;
35 }
36 
37 void dfs(int u){
38     for(int i=0; i<(int)g[u].size(); i++){
39         int v = g[u][i];
40         dfs(v);
41         Union(u,v); // 合并的时候是u合并到v上，u的父亲是v，利于下面寻找祖先，也就是所有u的父亲的祖先都是u
42         a[find(u)] = u; // u的所有孩子的祖先都是u
43     }
44     vis[u] = 1;
45     if(q1==u && vis[q2]) printf("%d\n",a[find(q2)]);
46     if(q2==u && vis[q1]) printf("%d\n",a[find(q1)]);
47     return ;
48 }
49 
50 int main(){
51     int T = read();
52     while(T--){
53         int n = read();
54         for(int i=0; i<=n; i++) {
55             g[i].clear();
56             f[i] = 0;
57             fa[i] = i;
58             vis[i] = 0;
59             a[i] = 0;
60         }
61         int u,v;
62         for(int i=1; i<n; i++){
63             scanf("%d%d",&u,&v);
64             f[v] = 1;
65             g[u].push_back(v);
66         }
67         cin >> q1 >> q2;
68         int i;
69         for(i=1; i<=n; i++)
70             if(f[i]==0) break;
71         dfs(i);
72     }
73 
74     return 0;
75 }

直接找：

 1 #include <cstdio>
 2 #include <cstring>
 3 #include <iostream>
 4 #include <algorithm>
 5 #include <vector>
 6 using namespace std;
 7 typedef long long ll;
 8 #define MS(a) memset(a,0,sizeof(a))
 9 #define MP make_pair
10 #define PB push_back
11 const int INF = 0x3f3f3f3f;
12 const ll INFLL = 0x3f3f3f3f3f3f3f3fLL;
13 inline ll read(){
14     ll x=0,f=1;char ch=getchar();
15     while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
16     while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
17     return x*f;
18 }
19 //
20 const int maxn = 1e4+10;
21 
22 vector<int> g[maxn];
23 int d[maxn],p[maxn],f[maxn];
24 
25 void dfs(int u,int fa,int de){
26     p[u] = fa;
27     d[u] = de;
28     for(int i=0; i<(int)g[u].size(); i++){
29         int v = g[u][i];
30         if(v == fa) continue;
31         dfs(v,u,de+1);
32     }
33 }
34 
35 int lca(int u,int v){
36     while(d[u] > d[v]) u = p[u];
37     while(d[v] > d[u]) v = p[v];
38     while(u != v){
39         u = p[u];
40         v = p[v];
41     }
42 
43     return u;
44 }
45 
46 int main(){
47     int T = read();
48     while(T--){
49         int n = read();
50         for(int i=0; i<=n; i++) {
51             g[i].clear();
52             f[i] = 0; d[i] = 0; p[i] = 0;
53         }
54         int u,v;
55         for(int i=1; i<n; i++){
56             scanf("%d%d",&u,&v);
57             f[v] = 1;
58             g[u].push_back(v);
59         }
60         int i;
61         for(i=1; i<=n; i++)
62             if(f[i]==0) break;
63         dfs(i,-1,0);
64         cin >> u >> v;
65         cout << lca(u,v) << endl;
66     }
67 
68     return 0;
69 }