题目解读
题目要求输出二叉树的所有路径(字符串形式),乍一看很简单,不就是二叉树的遍历嘛!其实不然,首先,我们用非递归的方式(C++)解决这道题(递归在产品代码中是不允许使用的,其次定位 bug 的时候非常困难)。这道题并非简单的 dfs(深度优先搜索),需要点技巧。
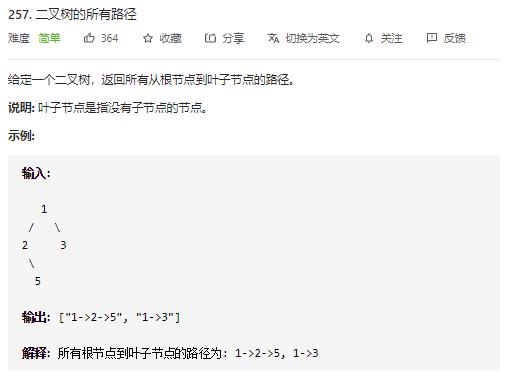
题目描述
标准 dfs 遍历输出 - 每次输出孩子节点
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector binaryTreePaths(TreeNode* root) {
if (root == nullptr) {
return {};
}
vector ans;
vector> allPath;
stack s;
vector path;
s.push(root);
path.push_back(root->val);
cout << path.back() << endl;
while (!s.empty()) {
TreeNode* curr = s.top();
s.pop();
if (curr->right != nullptr) {
path.push_back(curr->right->val);
s.push(curr->right);
cout << path.back() << endl;
}
if (curr->left != nullptr) {
path.push_back(curr->left->val);
s.push(curr->left);
cout << path.back() << endl;
}
}
return ans;
}
};
借助栈,上述代码实现了最简单的 dfs 遍历,结果如下:

标准 dfs 输出 - 每次输出孩子节点
栈中之所以先添加右叶子节点,是为了保证最终路径输出顺序从左往右。
标准 dfs 遍历输出 - 每次输出父亲节点
上述代码实现了标准 dfs 遍历,但显然不能满足题目要求,那该怎么处理呢?我们继续往下看。
class Solution {
public:
vector binaryTreePaths(TreeNode* root) {
if (root == nullptr) {
return {};
}
vector ans;
vector> allPath;
stack s;
vector path;
s.push(root);
path.push_back(root->val);
// cout << path.back() << endl;
while (!s.empty()) {
TreeNode* curr = s.top();
cout << curr->val << endl;
s.pop();
if (curr->right != nullptr) {
path.push_back(curr->right->val);
s.push(curr->right);
// cout << path.back() << endl;
}
if (curr->left != nullptr) {
path.push_back(curr->left->val);
s.push(curr->left);
// cout << path.back() << endl;
}
}
return ans;
}
};
上述代码中,我们打印栈顶每次弹出的元素,可以得到如下结果:

标准 dfs 输出 - 每次输出父节点
也就是说,每次只要某个节点的孩子节点都入栈了,该节点就可以不用考虑了。这个例子中,栈中初始节点是 1,然后加入其孩子节点 3、2,1 出栈;再加入节点 2 的孩子节点 5,2 出栈;以此类推。可是,这还无法得到题目要求的结果呀!不着急,我们离答案已经越来越近了。
二叉树的所有路径
通过观察发现:每次从栈顶弹出的节点,如果它没有孩子节点,那么这个节点就是叶子节点,而且遇到的第一个叶子节点也是最左边的叶子节点。我们把每次从栈顶弹出的节点记录下来,保存在 vector 中,那么遇到第一个叶子节点时,我们就得到最左边的一条路径(1->2->5).但是,接下来栈顶弹出的元素可是 3,想要得到一条完整的路径,必须将 3 和 1->2 拼接。或者说,要知道 3 之前弹出了哪些元素,我们把 3 之前栈顶弹出的元素 和 3 拼接,再与 3 之后的路径拼接起来,即可得到第二条路径。如何实现这点是这道题的关键所在。很容易想到的一点是,在输出的前一条路径(vector)基础上,不断将尾部元素丢弃,那什么时候停止丢弃呢?显然,丢弃直到第一条路径的尾部元素的右孩子节点是 3 即可。所以,path 这个 vector 中就不能记录节点的值了,而要记录节点的地址,因为值不是唯一的,而地址是唯一的。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector binaryTreePaths(TreeNode* root) {
if (root == nullptr) {
return {};
}
vector ans;
stack s;
vector path;
s.push(root);
string tmp;
while (!s.empty()) {
TreeNode* curr = s.top();
s.pop();
path.push_back(curr);
if (curr->right != nullptr) {
s.push(curr->right);
}
if (curr->left != nullptr) {
s.push(curr->left);
}
if (curr->left == nullptr && curr->right == nullptr) {
for (auto node : path) {
tmp += to_string(node->val);
if (node != path.back()) {
tmp += "->";
}
}
ans.push_back(tmp);
tmp.clear();
while (path.empty() == false && s.empty() == false && path.back()->right != s.top()) {
path.pop_back();
}
}
}
return ans;
}
};
这一次,终于得到了我们想要的结果了。上述代码中记录 string 的过程可以有更有效的方法,这里为了使代码的呈现更加容易理解,就不处理了,读者可以自己去研究下。









![index加载显示servlet数据_[WEB篇]-JavaWeb基础与应用-02-Servlet开发](http://pic.xiahunao.cn/index加载显示servlet数据_[WEB篇]-JavaWeb基础与应用-02-Servlet开发)









