课程推荐:6 线性规划模型基本原理与编程实现_哔哩哔哩_bilibili
目录
一、线性规划的实例与定义
1.1 线性规划的实例
1.2 线性规划的定义
1.3 最优解
1.4 线性规划的Mathlab标准形式
1.5 使用linprog函数
二、线性规划模型建模实战与代码
2.1 问题提出
2.2 基本假设
2.3 模型的分析与建立
2.3.1 模型分析
2.3.2 建立模型
2.3.3 多目标线性规划模型转化为单目标线性规划模型——制定界限
2.3.4 求解
在人们的生产实践中,经常会遇到如何利用现有资源来安排生产,以取得最大经济效益的问题。此类问题构成了运筹学的一个重要分支:数学规划。而线性规划(Linear Programming 简记LP)则是数学规划的一个重要分支。
一、线性规划的实例与定义
1.1 线性规划的实例
例:某机床厂生产甲、乙两种机床,每台销售后的利润分别为4千元与3千元。生产甲机床需用A、B机器加工,加工时间分别为每台 2小时和1小时;生产乙机床需用A、B、C三种机器加工,加工时间为每台各一小时。若每天可用于加工的机器时数分别为A机器10小时、B机器8小时和C机器7小时,问该厂应生产甲、乙机床各几台,才能使总利润最大?
上述问题的数学模型:设该厂生产x1台甲机床和x2乙机床时总利润z最大,则x1,x2应满足:
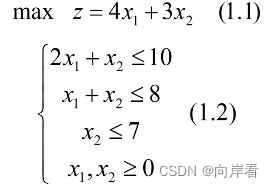
以上便是一个线性规划问题的数学模型,其中变量x1,x2称之为决策变量,(1.1)式被称为问题的目标函数,(1.2)中的几个不等式是问题的约束条件,记为s.t.(即subject to)。
1.2 线性规划的定义
目标函数及约束条件均为线性函数,故被称为线性规划问题。线性规划问题是在一组线性约束条件的限制下,求一线性目标函数最大或最小的问题。
1.3 最优解
满足约束条件的解x=[x,,L ,xI',称为线性规划问题的可行解,而使目标函数达到最大值的可行解叫最优解。
1.4 线性规划的Mathlab标准形式
线性规划的目标函数可以是求最大值,也可以是求最小值,约束条件的不等号可以是小于号也可以是大于号。为了避免这种形式多样性带来的不便,Matlab中规定线性规划的标准形式:
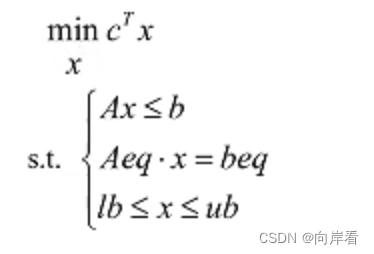
其中c和x为n维列向量,A、Aeq为适当维数的矩阵,b、beq为适当维数的列向量。
Matlab中求解线性规划的命令为:
Matlab中的linprog函数是一个线性规划求解器,可以用于求解线性规划问题。使用条件:满足Mathlab线性规划标准形式。
[x,fval] = linprog(c,A,b)
[x,fval] = linprog(c,A,b,Aeq,beq)
[x,fval] = linprog(c,A,b,Aeq,beq,lb,ub)
其中,x返回的是决策向量的取值,fval返回的是目标函数的最优值,c为价值向量,A,b对应的是线性不等式约束,Aeq,beq对应的是线性等式约束,lb和ub分别对应的是决策向量的下界向量和上界向量。
1.5 使用linprog函数

求解的Matlab程序如下:
f=[-2;-3;5];
a=[-2,5,-1;1,3,1]; b=[-10;12];
aeq=[1,1,1];
beq=7;
[x,y]=linprog(f,a,b,aeq,beq,zeros(3,1));
x, y=-y1. 目标函数中求max时,将目标函数的系数全部取反,即可看作求min,代入linprog函数,求得目标函数的最优值再取反回来,便得到了求max时目标函数的最优值(y)。这时,决策向量(x)的取值正对应着求max时目标函数的最优值,所以不变。
2. 约束条件中的不等号为大于号时,系数全部取反,代入linprog函数即可。
二、线性规划模型建模实战与代码
2.1 问题提出
市场上有n种资产
(i= 1,2,L ,n)可以选择,现用数额为M的相当大的资金作一个时期的投资。这n种资产在这一时期内购买
的平均收益率为
,风险损失率为
,投资越分散,总的风险越少,总体风险可用投资的
中最大的一个风险来度量。
购买时要付交易费,费率为
,当购买额不超过给定值
时,交易费按购买
计算。另外,假定同期银行存款利率是
,既无交易费又无风险(
= 5%)。
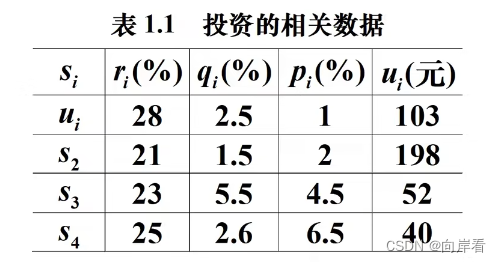
已知n=4时相关数据如表1.1。
试给该公司设计一种投资组合方案,即用给定资金M,有选择地购买若干种资产或存银行生息,使净收益尽可能大,使总体风险尽可能小。
2.2 基本假设
- (1)投资数额M相当大,为了便于计算,假设M=1。
- (2)投资越分散,总的风险越小。
- (3)总体风险用投资项目
中最大的一个风险来度量。
- (4)n+1 种
资产之间是相互独立的。其中s0表示存入银行的资产。
- (5)在投资的这一时期内,
,
,
为定值,不受意外因素影响。
- (6)净收益和总体风险只受
,
,
影响,不受其它因素干扰。
2.3 模型的分析与建立
2.3.1 模型分析
- 1. 首先,我们要明确两个目标,即收益最大和风险最小,因此这是一个多目标规划模型。
- 2. 总体风险用所投资的
中最大的一个风险来衡量,即
- 3. 购买
(i= 1,L ,n) 所付交易费是一个分段函数,即
![]()
而所给的定值 (单位:元)相对总投资M很小,
更小可以忽略不计,这样购买
的净收益可以简化为
。
2.3.2 建立模型
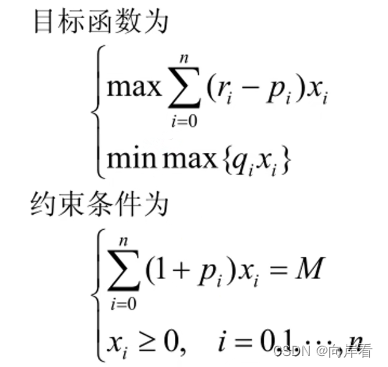
其中, 表示投资项目
的资金,i= 0,1,…,n;x0表示存入银行的资产。约束条件表示总资金投入必须等于M,投资项目
的资金必须大于等于0。
2.3.3 多目标线性规划模型转化为单目标线性规划模型——制定界限
方案一:固定风险水平,优化收益
在实际投资中,投资者承受风险的程度不一样, 若给定风险一个界限a,使最大的一个风险,可找到相应的投资方案。这样把多目标规划变成一个目标的线性规划。
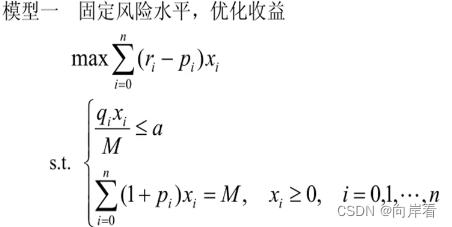
方案二:固定盈利水平,极小化最大风险
给定收益一个界限k。
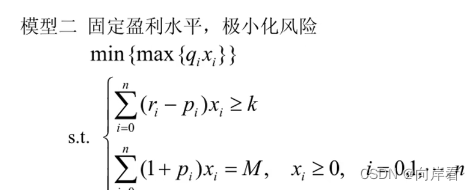
方案三:设置投资偏好系数
投资者在权衡资产风险和预期收益两方面时,希望选择一个令自己满意的投资组合。因此对风险、收益分别赋予权重s (0<s≤1)和1-s,s称为投资偏好系数。
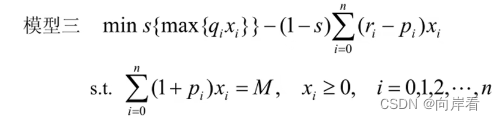
2.3.4 求解
模型一:

由于a是任意给定的风险度,没有一个确定的准则,不同的投资者有不同的风险度。我们从a= 0开始,以步长 = 0.001进行循环搜索,编制程序如下:
clc,clear
a=0;hold on
while a<0.05c=[-0.05,-0.27,-0.19,-0.185,-0.185];A=[zeros(4,1 ),diag([0.025,0.015,0.055,0.026])];b=a*ones(4,1);Aeq=[1,1.01,1.02,1.045,1.065];beq=1; LB= zeros(5,1);[x,Q]=linprog(C,A,b,Aeq,beq,LB);Q=-Q; plot(a,Q,'*k');a=a+0.001;
end
xlabel('a'),ylabel('Q')
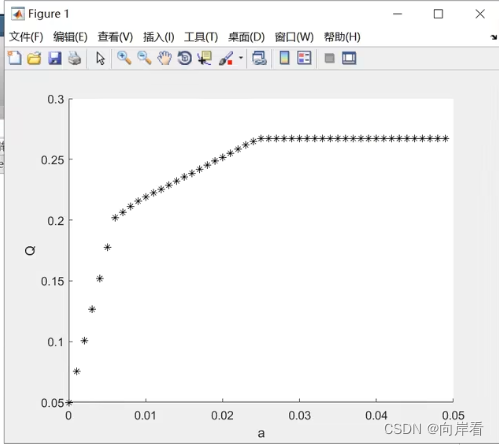
可以看出,在a=0.006附近有一个转折点,在这一点左边,风险增加很少时,利润增长很快。在这一点右边,风险增加很大时,利润增长很缓慢,所以对于风险和收益没有特殊偏好的投资者来说,应该选择曲线的转折点作为最优投资组合,所对应投资方案为风险度a= 0.006,收益Q=0.2019,x0=0,x1= 0.24,x1= 0.4,x3= 0.1091,x4= 0.2212。
)



)






)
)






