(一)前言

所谓的字符串匹配就是在一个长字符串(可称文本T)中找一个短字符串(可称模式P)，看长字符串中是否存在短字符串，若存在则返回出现的第一个位置，若不存在则返回一个标记。字符串搜索算法有很多，比较知名的自然是大名鼎鼎Knuth-Morris-Pratt 算法(简称 KMP)和Boyer-Moore(简称BM)。关于这两个算法的实现比较复杂，需要很多的前置知识，不在这里长篇大论，有兴趣的同学，可自行搜索。

今天给大家介绍一个相对高效且简单的Horsepool算法，Horsepool算法是Boyer-Moore算法的简化版本，为了方便理解Horsepool算法，我们先从朴素字符串匹配算法谈起。

(二)朴素(暴力)字符串匹配算法

先看朴素的字符串匹配算法的过程：

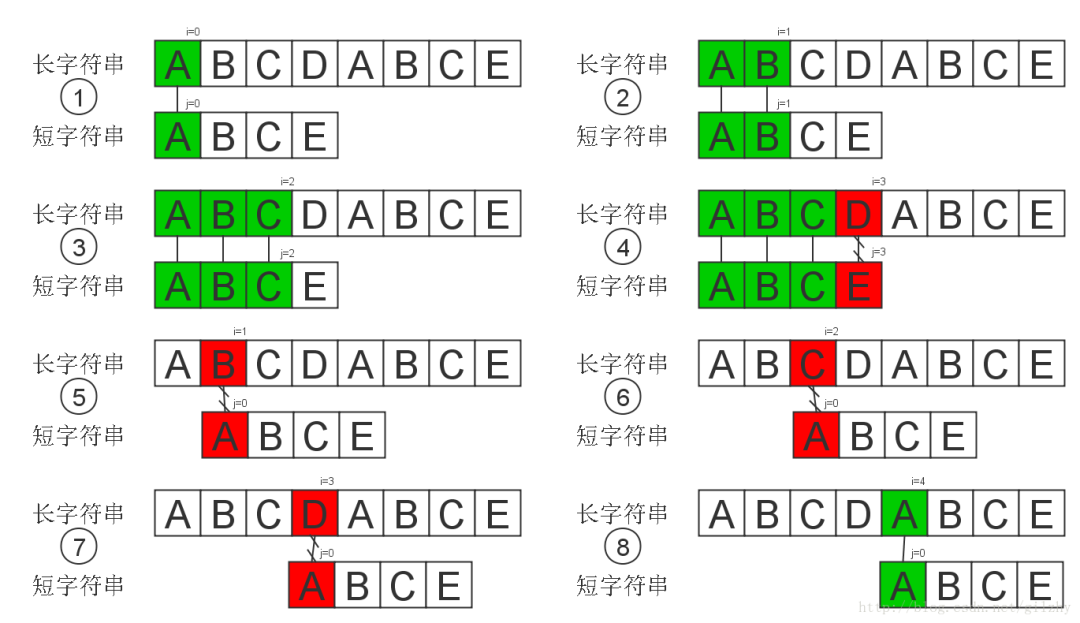算法规则：用i，j表示两字符串正在比较的字符位置。若长字符串与短字符串该位置字符匹配，则继续比较二者后面的字符，即i加1，j加1。不匹配，分别回溯i，j。这个算法非常朴素，通常性能极差。最坏情况举例：aaaaaaaab和aaab匹配，需要重复比较字符多次。

朴素搜索Python实现：

# txt 长字符串，pat 短字符串def forceSearch(txt, pat):    M = len(txt)    N = len(pat)    for i in range(M-N+1):        for j in range(N):            if txt[i+j]!=pat[j]:                break        else:            return i    return 

(三)Horspool算法

Horspool算法把短字符串(以下简称模式P)与长字符串(以下简称文本T)的开头字符对齐，从模式P的最后一个字符开始比较，如果尝试比较失败了，它把模式P向后移。每次尝试过程中比较是从右到左的。

假设对齐后文本T中最后一个对齐字符为X(代表任意字符)，Horspool算法根据X的不同情况来确定移动距离(朴素算法每次不匹配只右移一位)，无论X是否和模式的最后一个字符相匹配，一般来说，会存在下面四种情况：

情况1，如上图所示，对齐后，文本T中最后一个字符对齐X为o，与模式P最后一个字符g不匹配，且模式P中不存在X(也就是字母o)，模式P的移动长度就是它的全部长度，移到所示的位置。

情况2，如上图所示，对齐后，文本T的最后一个对齐字符X为e，恰好和模式P最后一个字符匹配。但是从右向左比较时，有字符不匹配，比如此时的o和a不匹配。由于模式P中只包含一个字符X(也就是e)，模式P的移动长度就是它的全部长度，移到所示的位置。

情况3，如上图所示，对齐后，文本T的最后一个对齐字符X为a，与模式P最后一个字符g不匹配。移动时应该把模式P中最右边的X(a)和文本中的X(a)对齐。

情况4，如上图所示，对齐后，文本T的最后一个对齐字符X为a，与模式P最后一个字符a匹配，但是从右向左比较时，有字符不匹配，比如此时的n和i不匹配。移动时，应把模式P除X(a)外，最右边字符X(a)和文本T中的X(a)对齐。

综上所述，比起朴素算法每次总是移动一个位置，从右到左的字符比较使模式不匹配时可以移动得更远。然而，如果在每次尝试时都必须检查模式P中的每个字符来确定移动距离，它的优势也会丧失殆尽。我们可以预先算出遇到某个字符要移动的距离，并把它存在一个表中。

示例如下，对于模式BARBER，移动距离如下表所示：

这里对字符A，B做一下解释，方便还没有理解的同学，加深理解。

若对齐后，文本T的最后一个对齐字符X为A，A与R不匹配，BARBER，A与结尾处R字符距离为4。

若对齐后，文本T中最后一个对齐字符X为B，B与R不匹配，BARBER，最右边B与结尾处R字符距离为2。

若对齐后，文本T中最后一个对齐字符X不在模式P中，则移动距离为模式P长度6。

Horspool算法Python实现：

def horspool(txt,pat):    n = len(txt)    m = len(pat)    table = [m]*96 #ascii中可打印字符有96，且前32为控制字符    for i in range(m - 1):        table[ord(pat[i]) - 32 ] = m -1 - i        #从左至右扫描模式，相同字符的最后一次改写恰好是该字符在模式串的最右边    i = m - 1    while i <= n - 1:        k = 0        while k <= m-1 and pat[m - 1 - k] == txt[i - k]:            k += 1                       #向左比较下一个字符        if k == m:            return  i - m + 1            #匹配成功返回索引        else:            i += table[ord(txt[i]) - 32] #根据表格移动模式串    return -1

(四)参考文献

[1]https://blog.csdn.net/khwkhwkhw/article/details/51288502

[2]https://www.runoob.com/python/python-for-loop.html

[3]https://www.asklib.com/view/fbef10420ab8.html

[4]https://blog.csdn.net/gilzhy/article/details/16803993

[5]https://ethsonliu.com/2018/04/kmp.html