逻辑斯蒂回归_逻辑斯蒂回归详细解析 | 统计学习方法学习笔记 | 数据分析

逻辑斯蒂回归_逻辑斯蒂回归详细解析 | 统计学习方法学习笔记 | 数据分析 | 机器学习...

本文包括：

重要概念
逻辑斯蒂回归和线性回归
二项逻辑斯谛回归模型
逻辑斯蒂回顾与几率
模型参数估计
多项逻辑斯谛回归
其它有关数据分析，机器学习的文章及社群

1.重要概念：

在正式介绍逻辑斯蒂回归模型之前，需要先对一些基本概念有所了解，如果明白这些概念可以直接跳过。

分布函数和密度函数：对于一个连续型随机变量，密度函数是指该变量在其可取值范围内为一个特定值的概率，分布函数即在一个特定值和小于该特定值的范围内出现的概率，可以理解为密度函数的面积比率。

用逻辑斯蒂分布举例来说（下图），在密度函数中，可以看到在x=0时出现峰值，即x取0的概率最大，从0开始往无穷小和无穷大都在递减。再看分布函数，可以看到当x=0时，密度函数取值为0.5，对照密度函数，在小于等于0的部分，面积是总面积的一半。

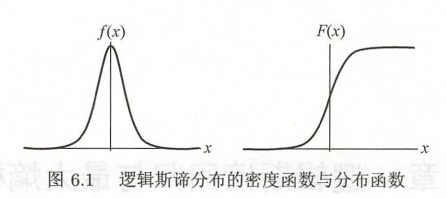
似然函数：在统计学中，概率描述了已知参数时的随机变量的输出结果，似然则用来描述已知随机变量输出结果时，未知参数的可能取值。那么似然函数就是用来求得未知参数的估计值所使用的函数。

极大似然估计：通过最大化似然函数求得未知参数的估计值。这里讲一下为什么是极大而非其它的方法求参数的估计值。

在机器学习中，我们有大量的记录构成训练集，需要根据训练集进行学习获得模型，根据具体的问题，我们可以将一个特定的模型套用在这个具体问题中。现在，我们有了一个含有未知参数的模型，以及大量训练集记录。

根据模型，我们可以假设Y=1的概率为P，Y=0的概率为1-P（这里的P包含了模型中的未知参数）。假设训练集中有10个记录，3个为1，7个为0，那么得到这个最终结果的概率为P^3*(1-P)^7。

现在重点来了，既然现实情况中已经出现了3个1和7个0的情况，那么我们的模型应该让这种情况出现的概率最大，因为毕竟这个结果已经出现了。

也就是说，我们应当最大化P^3*(1-P)^7，以此推得P中所包含的未知参数的估计值，并最终得到我们想要的模型。

2.逻辑斯蒂回归和线性回归：

在线性回归（感知机）中，我们知道一个分离超平面w·x将特征空间分成两个部分，实例在不同的子空间中则被分为相对应的类。但是线性回归的一个问题在于，我们不知道一个新输入的实例，它属于一个类的概率是多少。

换句话说，新输入实例在特征空间中的位置可能与分离超平面距离非常近，也有可能非常远，如果距离较远，那么它更有可能被分成它所在一侧对应的类，但是如果与超平面的距离非常近，说明它被分成另一类的可能性也很大，比如被分成A的可能性为51%，而分成B类的可能性为49%，此时线性回归会将其分为A类，而忽略了49%分成B类的可能性，也就是说，线性回归仅给出结论，未给出概率。

于是，为了得到这一概率，我们引入了Sigmoid函数：

Sigmoid函数能够将线性回归产生的值(-∞，+∞)转换到(0,1)区间内，而概率的取值也在(0,1)内，这样，就可以显示一个实例被分为一个类的概率是多少了。

3.二项逻辑斯谛回归模型：

首先来看逻辑斯蒂函数的一般形式，其分布具有以下分布函数和密度函数：

式中，μ为位置参数，γ>0为形状参数。

分布函数以（μ,1/2）为中心对称，满足：

形状参数γ的值越小，分布函数曲线在中心附近增长得越快。

现在，我们让μ取0，γ取1，即得到我们在逻辑斯蒂回归中使用的函数：

采用上式，我们将线性回归产生的值代入到sigmoid函数之中，可得：

二项逻辑斯谛回归模型是一种分类模型，由条件概率分布P(Y|X）表示。这里，随机变量x取值为实数，随机变量Y取值为1或0。

这样，我们就将范围为实数的线性回归产生的值转变为逻辑斯蒂回归中仅在(0,1)范围之内。

逻辑斯谛回归仅对二分类的问题有效，我们可以比较P(Y=1|x)和P(Y=0|x)两个条件概率值的大小，将实例x分到概率较大的那一类，同时也能得知分成两种类别的可能性是多少。